Дано: f (x), g (x) определены на (x0,b) и
1) 
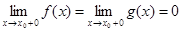
2) f,g дифференцируемы на (x0,b)
3) g ¢ (x) ¹0 на (x0,b).
Тогда
,
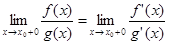если существует конечный или бесконечный предел
.
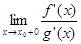Доказательство. Доопределим f, g в точке x0 по непрерывности нулем f (x0) =g (x0) =0. По тереме Коши, примененной к отрезку [x0,x], будет существовать x (x) Î (x0,x): x0< x (x) < x и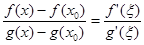 
, из условия x0< x (x) <x следует, что 
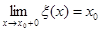, причем x (x) ¹x0, если x ¹x0. По теореме о существовании предела суперпозиции
= 
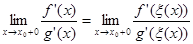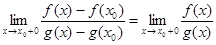ч. т.д.
Замечание. Аналогично это утверждение доказывается для левой окрестности. Откуда получаем утверждение для x ® x0.
Следствие 1. Если
1) Существуют f (k),g (k), k=1,2,…,n на (x0,b)
2) 
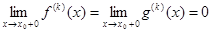, k=0,1,…,n-1
3) Существуeт g (n) (x) ¹0 на (x0,b), то
,
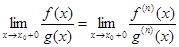если
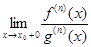
существует, конечный или бесконечный.
Следствие 2. Если f, g дифференцируемы для x>a,
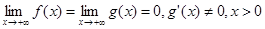, то
,
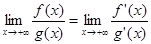если последний существует, конечный или бесконечный.
Доказательство. Сделаем замену
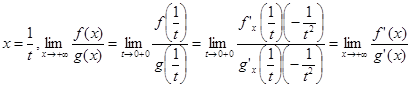
Замечание. Аналогичные утверждения имеют место для x ® - ¥.
3.2 Раскрытие неопределенностей вида ¥/¥
f,g определены на (x0,b) и
1) 
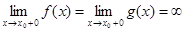
2) f,g дифференцируемы на (x0,b)
3) g ¢ (x) ¹0 на (x0,b)
Тогда
,
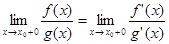если последний существует конечный или бесконечный.
Замечание. Аналогичные утверждения имеют место для x ® x0 - 0, x ® x0, x ® + ¥, x ® - ¥.
3.3 Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
В некоторых случаях порядок бесконечно малой или бесконечно большой можно определить, последовательно вычисляя производные. Предположим, что f (x) - бесконечно малая при x ® x0 и в точке x0 обращаются в ноль все производные до (n-1) - го порядка включительно f (x0) =0, f ¢ (x0) =0,…, f (n-1) (x0) =0 и f (n) (x0) ¹0. В этом случае порядок этой бесконечно малой будет равен n. При этом главная часть будет равна
.
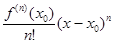Это утверждение следует из равенства
,
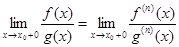в котором в качестве функции g (x) берется (x-x0) n.
.
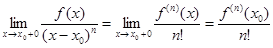Похожее утверждение можно сформулировать и для бесконечно больших функции.
Пример: f (x) = 3sh x - 3sin x - x3 при x ® 0
f ¢ (x) =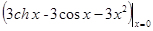 
=0,f ¢¢ (x) = 
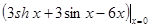=0,f ¢¢¢ (x) = 
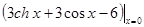=0,f (4) (x) = 
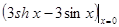=0,f (5) (x) = 
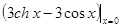=0,f (6) (x) = 
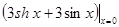=0,f (7) (x) = 
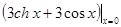=6 ¹ 0.
Таким образом, порядок этой бесконечно малой равен 7 и f (x) ~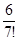 
x7, x ®0.
3.4 Раскрытие неопределенностей вида 0¥, 1¥, 00,¥0,¥ - ¥
Неопределенности вида 0 ¥ сводятся к уже рассмотренным.
Примеры.
1) 
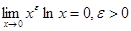
2) 
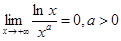
3) 
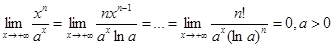
4) ¥ - ¥
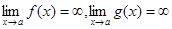
Можно, например, так
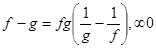
5) Неопределенности вида 1 ¥,00, ¥0 сводятся к уже рассмотренным логарифмированием
y=uv=ev ln u
Пример 1.
.
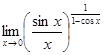Вычисление.
.
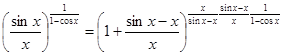Этот предел рассматриваем, как
,
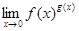где
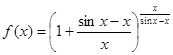, а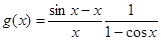 
.
Из теоремы о существовании предела суперпозиции двух функций следует, что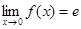 
. Далее
,
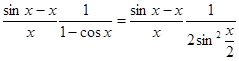заменяя знаменатель на эквивалентную бесконечно малую получим
= 
.
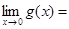
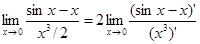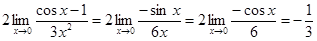Таким образом,
.
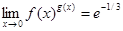Пример 2.
.
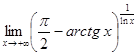Представим функцию в следующем виде.
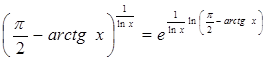
и вычислим предел
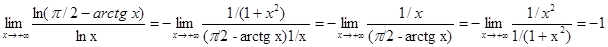
Пример 3. Вычислить предел:
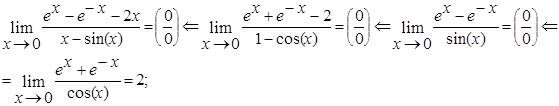
Пример
4. 
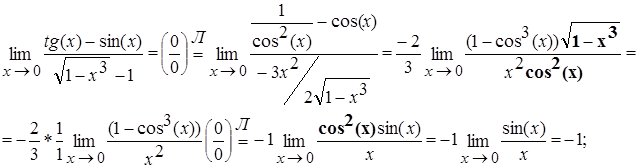
Пример 5.
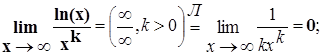
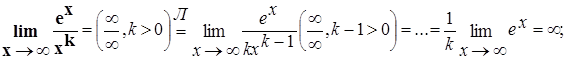
При х ® ¥
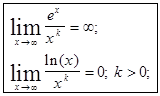
при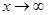 
ex возрастает быстрее любой степенной функции хк, k>0
Дата: 2019-04-23, просмотров: 176.
