ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им.Ф. СКОРИНЫ
Математический факультет
Кафедра математического анализа
Применение производной при нахождении предела
Курсовая работа
Исполнитель Бурцева Е.А.
студентка группы М-43
Научный руководитель Астапович Г.Е.
ГОМЕЛЬ 2009
Содержание
Введение
1. Бесконечно малые и их сравнения; символы "o малое" и "о большое"
2. Основные теоремы дифференциального исчисления
2.1 Теорема Ферма о нуле производной
2.2 Теорема Ролля о нуле производной
2.3 Теорема Лагранжа о конечных приращениях
2.4 Теорема Коши о конечных приращениях
3. Раскрытие неопределенностей. правило лопиталя
3.1 Раскрытие неопределенностей вида 0/0
3.2 Раскрытие неопределенностей вида ¥/¥
3.3 Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
3.4 Раскрытие неопределенностей вида 0¥, 1¥, 00,¥0,¥ - ¥
4. Формула тейлора. вычисление пределов с помощью формулы тейлора
4.1 Многочлен Тейлора. Формула Тейлора с остаточным членом Rn.
4.2 Остаток в форме Пеано
4.3 Другие формы остатка в формуле Тейлора
4.4 Разложение некоторых элементарных функций по формуле Тейлора
4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
4.6 Формула Тейлора для четных и нечетных функций
Заключение
Список использованных источников
Введение
Данная курсовая работа раскрывает применение производной при вычислении пределов. Вычисление пределов важная часть математического анализа, поскольку практически весь курс математического анализа опирается на понятие предела.
Действительно, производная, интеграл, непрерывность функции - все эти понятия используют предел.
Курсовая работа состоит из четырех разделов.
В первом разделе раскрывается понятие скорости роста функции, вводятся символы "О большое" и "о малое", и важное понятие, для вычисления пределов, эквивалентные функции.
Во втором разделе приведены основные теоремы дифференциального исчисления, служащие необходимой основой для правила Лопиталя и формулы Тейлора.
В третьем разделе приведено правило Лопиталя и методы раскрытия всех типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон].
В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов.
1. Бесконечно малые и их сравнения; символы "o малое" и "о большое"
Определение. Бесконечно малой в x0 называется функция f (x) такая, что 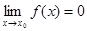
Свойства бесконечно малых функций:
1) Критерий существования конечного предела функции
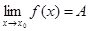 Û $ б. м. функция a ( x) при x ® x0: f ( x) = A+ a ( x)
Û $ б. м. функция a ( x) при x ® x0: f ( x) = A+ a ( x)
2) a ( x), b ( x) б. м. Þ a ( x) + b ( x) б. м.
3) Произведение бесконечно малой функции на ограниченную является бесконечно малой функцией.
4) Произведение бесконечно малых функций является бесконечно малой функцией.
Определение. f (x) определенная в проколотой окрестности x0 называется бесконечно большой в т. x0, если  .
.
5) Если a ( x) б. м. при x ® x0 и a ( x) ¹0, то 1/ a ( x) является бесконечно большой и наоборот. Символически это записывают в виде 1/ ¥=0, 1/0= ¥.
Остаток в форме Пеано
Теорема 1. Если функция f (x) (n-1) - раз дифференцируема в окрестности U= (x0-a,x0+a) точки x0 и существует f (n) (x0), то имеет место равенство
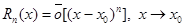 .
.
Другими словами
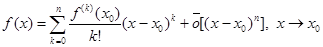
 (5)
(5)
Доказательство. Для краткости будем обозначать R (x) =Rn (x)
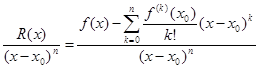 (10)
(10)
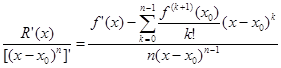 (11)
(11)
 (1m)
(1m)
…
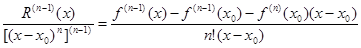 (1n-1)
(1n-1)
f (n-1) (x) дифференцируема в точке x0, поэтому
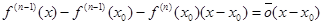
Откуда
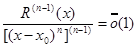
По правилу Лопиталя
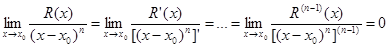
Теорема 2. (Единственность представления функции по формуле Тейлора) Если f имеет n-ю производную в точке x0 и
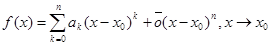 ,
,
то 
Лемма. Если
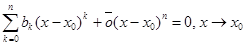 , (2)
, (2)
то bk=0, k=0,1,…,n
Доказательство. в (2) перейдем к пределу при x ® x0, получим
b0 = 0, 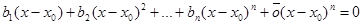 ,
,
делим полученное выражение на (x-x0) и переходим к пределу при x ® x0 и т.д.
Доказательство теоремы.
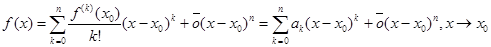
откуда и следует утверждение.
Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
Из формул Тейлора следуют известные "равносильности при 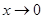 "; например,
"; например,
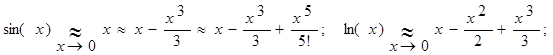
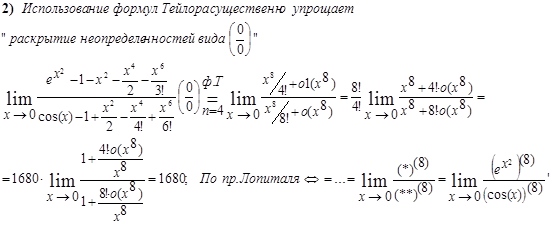
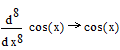

Пример 1.
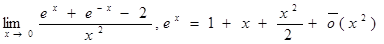
Пример 2.
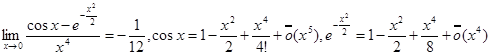 .
.
Пример 3. Разложить функцию f (x) = 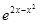 по формуле Тейлора с остатком Пиано по степеням x до x5 включительно.
по формуле Тейлора с остатком Пиано по степеням x до x5 включительно.
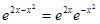 . Для решения задачи возьмем разложения функции
. Для решения задачи возьмем разложения функции
e2x = 1+2x+ 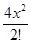 +
+ 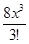 +
+ 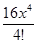 +
+ 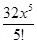 +o (x5),
+o (x5),
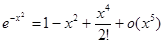
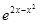 = (1+2x+
= (1+2x+ 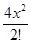 +
+ 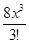 +
+ 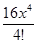 +
+ 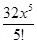 +o (x5)) (
+o (x5)) ( 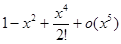 ) =
) =
1+2x+ 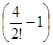 x2+
x2+ 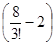 x3+
x3+ 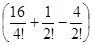 x4+
x4+ 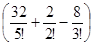 x5+o (x5) =
x5+o (x5) =
1+2 x+ x2 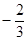 x3
x3 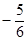 x4
x4 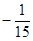 x5+ o ( x5).
x5+ o ( x5).
Пример 4. Разложить функцию f (x) =1/cos x по формуле Тейлора с остатком Пиано по степеням x до x5 включительно. Представим функцию в виде
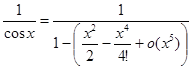 =1+u+u2+u3+o (u3), где u =
=1+u+u2+u3+o (u3), где u = 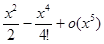 .
.
Тогда
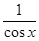 =1+u+u2+u3+o (u3) =1+
=1+u+u2+u3+o (u3) =1+ 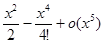 +
+ 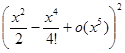 +
+ 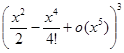 +
+ 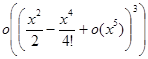 .
.
При вычислении степеней
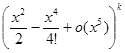
нас интересуют только слагаемые степеней не выше x5, более высокие степени войдут в o (x5). Таким образом,
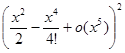 =
= 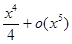 ,
, 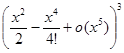 =
= 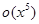 ,
, 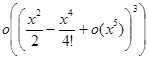 =
= 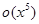 .
.
Выражение
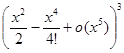 =
= 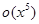
показывает, что в разложении
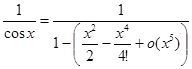 =1+u+u2+u3+o (u3)
=1+u+u2+u3+o (u3)
можно, с самого начала, ограничится второй степенью
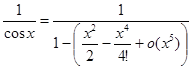 =1+u+u2+o (x5).
=1+u+u2+o (x5).
Подставляя нужные выражения в это равенство получим
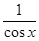 =1+
=1+ 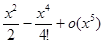 +
+ 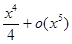 +
+ 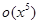 =1+
=1+ 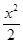 +
+ 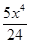 +
+ 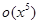 .
.
Пример 5. Используя разложение из предыдущего примера, разложить функцию f (x) =tg x по формуле Тейлора с остатком Пиано по степеням x до x6 включительно.
tg x= 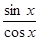 =
=
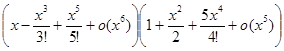 =
=
x+x2 (0) +x3 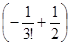 +x4 (0) +x5
+x4 (0) +x5 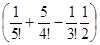 +x6 (0) =
+x6 (0) =
= 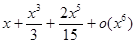
Пример 6. Разложить функцию f (x) = (1+x) a - (1 - x) a по формуле Тейлора с остатком Пиано.
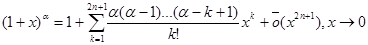
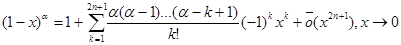
k = 2l+1, 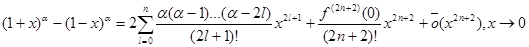
Таким образом,
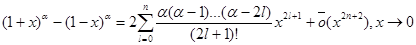
Следствие. 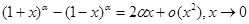
Пример 7. Используя следствие из предыдущего примера, найти предел (1401)
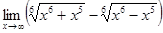 .
.
Имеем:
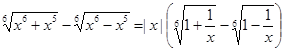 =|x|
=|x| 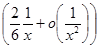 =
= 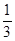 sign x +o (
sign x +o ( 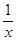 ).
).
Пример 8. Разложить функцию
f (x) = 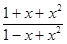
по формуле Тейлора с остатком Пиано по степеням x до x4 включительно.
Сначала выпишем разложение функции 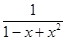 по степеням x до x3 включительно.
по степеням x до x3 включительно.
Положим u=x - x2, тогда
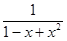 =
= 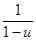 =1+ u+ u2+ u3+ o ( u3) =1+ x - x2+ ( x - x2) 2+ ( x - x2) 3+ o ( x3) =1+ x - x3 + o ( x3).
=1+ u+ u2+ u3+ o ( u3) =1+ x - x2+ ( x - x2) 2+ ( x - x2) 3+ o ( x3) =1+ x - x3 + o ( x3).
Далее,
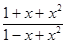 =
= 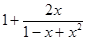 =1+2 x (1+ x - x3 + o ( x3)) =1+2 x+2 x2-2 x4+ o ( x4).
=1+2 x (1+ x - x3 + o ( x3)) =1+2 x+2 x2-2 x4+ o ( x4).
Второй способ. Так как
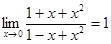 ,
,
то на первом шаге выделяем единицу:
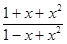 =
= 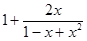 .
.
Второе слагаемое представляем в виде Cxng2 (x) так, чтобы 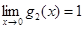 , после чего следует представить функцию g2 (x) в виде g2 (x) = 1+g3 (x) и т.д. В нашем случае:
, после чего следует представить функцию g2 (x) в виде g2 (x) = 1+g3 (x) и т.д. В нашем случае:
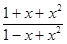 =
= 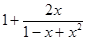 =
= 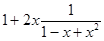 =
= 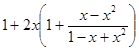 =
=
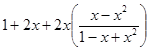 =
= 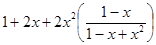 =1+2x+
=1+2x+ 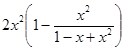 =
=
1+2x+2x2 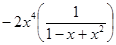 =1+2x+2x2-2x4+o (x4).
=1+2x+2x2-2x4+o (x4).
Заключение
В данной курсовой работе были рассмотрены методы вычисления пределов использующие понятие производной, а именно: правило Лопиталя и формула Тейлора.
Для каждого метода рассмотрены примеры вычисления пределов. Так же было рассмотрено такое важное понятие, как скорость роста функции, играющее большую роль при вычислении пределов.
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им.Ф. СКОРИНЫ
Математический факультет
Кафедра математического анализа
Применение производной при нахождении предела
Курсовая работа
Исполнитель Бурцева Е.А.
студентка группы М-43
Научный руководитель Астапович Г.Е.
ГОМЕЛЬ 2009
Содержание
Введение
1. Бесконечно малые и их сравнения; символы "o малое" и "о большое"
2. Основные теоремы дифференциального исчисления
2.1 Теорема Ферма о нуле производной
2.2 Теорема Ролля о нуле производной
2.3 Теорема Лагранжа о конечных приращениях
2.4 Теорема Коши о конечных приращениях
3. Раскрытие неопределенностей. правило лопиталя
3.1 Раскрытие неопределенностей вида 0/0
3.2 Раскрытие неопределенностей вида ¥/¥
3.3 Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
3.4 Раскрытие неопределенностей вида 0¥, 1¥, 00,¥0,¥ - ¥
4. Формула тейлора. вычисление пределов с помощью формулы тейлора
4.1 Многочлен Тейлора. Формула Тейлора с остаточным членом Rn.
4.2 Остаток в форме Пеано
4.3 Другие формы остатка в формуле Тейлора
4.4 Разложение некоторых элементарных функций по формуле Тейлора
4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
4.6 Формула Тейлора для четных и нечетных функций
Заключение
Список использованных источников
Введение
Данная курсовая работа раскрывает применение производной при вычислении пределов. Вычисление пределов важная часть математического анализа, поскольку практически весь курс математического анализа опирается на понятие предела.
Действительно, производная, интеграл, непрерывность функции - все эти понятия используют предел.
Курсовая работа состоит из четырех разделов.
В первом разделе раскрывается понятие скорости роста функции, вводятся символы "О большое" и "о малое", и важное понятие, для вычисления пределов, эквивалентные функции.
Во втором разделе приведены основные теоремы дифференциального исчисления, служащие необходимой основой для правила Лопиталя и формулы Тейлора.
В третьем разделе приведено правило Лопиталя и методы раскрытия всех типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон].
В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов.
1. Бесконечно малые и их сравнения; символы "o малое" и "о большое"
Определение. Бесконечно малой в x0 называется функция f (x) такая, что 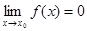
Свойства бесконечно малых функций:
1) Критерий существования конечного предела функции
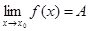 Û $ б. м. функция a ( x) при x ® x0: f ( x) = A+ a ( x)
Û $ б. м. функция a ( x) при x ® x0: f ( x) = A+ a ( x)
2) a ( x), b ( x) б. м. Þ a ( x) + b ( x) б. м.
3) Произведение бесконечно малой функции на ограниченную является бесконечно малой функцией.
4) Произведение бесконечно малых функций является бесконечно малой функцией.
Определение. f (x) определенная в проколотой окрестности x0 называется бесконечно большой в т. x0, если  .
.
5) Если a ( x) б. м. при x ® x0 и a ( x) ¹0, то 1/ a ( x) является бесконечно большой и наоборот. Символически это записывают в виде 1/ ¥=0, 1/0= ¥.
Дата: 2019-04-23, просмотров: 359.