f,g определенны в некоторой проколотой окрестности x0
Пишут
,
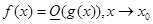Если
.
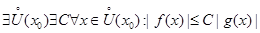Аналогично определяется O при x ® x0+0, x ® x0 - 0, x ® ± ¥, x ® ¥.
Пример: f ( x) = O (1), x ® ¥ означает локальную ограниченность функции в ¥.
Опр. Если при x ® x0, f ( x) = O ( g) и g ( x) = O ( f), то f ( x), g ( x) называются функциями одного порядка.
Пример: Функции x3, x2 являются функциями одного порядка при x ®1.
Определение o. Пусть f ( x), g ( x) определенны в некоторой проколотой окрестности точки x0, пишут f ( x) = o ( g ( x)), x ® x0, если
$ 
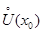$ б. м. a ( x) при x ® x0, такая, что " x Î 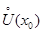: f ( x) = a ( x) g ( x)
Аналогично определяется o при x ® x0+0, x ® x0 - 0, x ® ± ¥, x ® ¥.
Пример: f ( x) = o (1), при x ® x0 означает, что f ( x) бесконечно малая при x ® x0.
Некоторые примеры работы с символами o (подразумевается x ®0).
o ( xn) ± o ( xn) = o ( xn)
xm o ( xn) = o ( xn+ m)
c o ( xn) = o ( xn) ( c-константа)
o ( xn) ± o ( xn+ p) = o ( xn), здесь p натуральное.
o ( xn+ p) / xp= o ( xn) В частности, o ( xp) / xp= o (1).
o (an xn ± an+1 xn+1 ± … ± an+p xn+p) = o (xn)
Если a, b б. м. и b= o ( a), то говорят, что b бесконечно малая более высокого порядка, чем a.
Определение. Функции f ( x), g ( x) называются эквивалентными в x0 (говорят так же, в окрестности x0), если выполнено хотя бы одно из двух условий
f (x) =g (x) +o (g (x)), x ® x0
g (x) =f (x) +o (f (x)), x ® x0.
Условие эквивалентности записывается в виде f ~ g, при x ® x0.
Замечание 1. Если выполнено одно из этих условий, то будет выполнено и второе.
Замечание 2. Эти условия можно записать в другой форме. Например, первое из них: в некоторой проколотой окрестности точки имеет место равенство
f ( x) = h ( x) g ( x),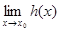 
=1.
Замечание 3. Если, например, g ( x) ¹0, то первое условие можно записать в виде
.
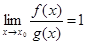Определение. Если f ( x) ~ ( x- x0) n при x ® x0, то f (x) называется бесконечно малой порядка n при x ® x0.
Если f ( x) ~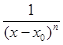 
при x ® x0, то f (x) называется бесконечно большой порядка n при x ® x0.
Если f ( x) бесконечно большая при x ® ¥ и f ( x) эквивалентна xn при x ® ¥, то f (x) называется бесконечно большой порядка n при x ® ¥.
Замечание. Если f ( x) бесконечно малая порядка n, то 1/ f ( x) будет бесконечно большой порядка n и наоборот.
Примеры. Определить характер функций
, 
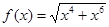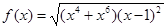в 0, 1,+ ¥.
При вычислении пределов полезна следующая теорема
Теорема 2. Пусть f эквивалентна f1, g эквивалентна g1 при x ® x0.
Если существует предел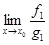 
, тогда существует и 
.
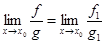Если существует предел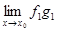 
, тогда существует и 
.
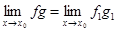Определение. Если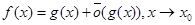 
, то g называется главной частью f при x ® x0.
Основные теоремы дифференциального исчисления
Теорема Ферма о нуле производной
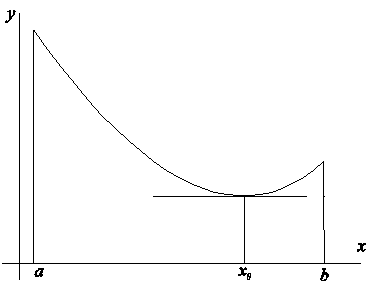
Теорема. Если f (x) - определена на (a,b) и дифференцируема в точке x0 Î (a,b), принимает в точке x0 наибольшее или наименьшее значение, то f ¢ (x0) =0.
Доказательство. Для случая наименьшего значения
f ¢ (x0+0) =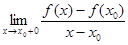 
³ 0, f ¢ (x0-0) = 
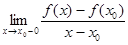£ 0 Þ f ¢ (x0) =0
Геометрическая интерпретация
Дата: 2019-04-23, просмотров: 231.
