Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

А.А. Халафян

 

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

 

тексты лекций

 

 

Краснодар 2008

 

Статистическое определение вероятности

Существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения. В первую очередь это события с неравновозможными исходами (например, игральная кость «нечестная», монета сплющена и т.д.). В таких случаях может помочь статистическое определение вероятности, основанное на подсчете частоты наступления события в испытаниях.

Определение 2. Статистической вероятностью наступления события А называется относительная частота появления этого события в n произведенных испытаниях [4], т.е.

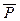(А) = W(A) = m / n,

где 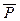(А) – статистическое определение вероятности; W(A) – относительная частота; n – количество произведенных испытаний; m – число испытаний, в которых событие А появилось. Заметим, что статистическая вероятность является опытной, экспериментальной характеристикой.

Причем при n → ∞, 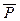(А) → P(А), так, например, в опытах Бюффона (XVIII в.) относительная частота появления герба при 4040 подбрасываниях монеты, оказалось 0,5069, в опытах Пирсона (XIX в.) при 23000 подбрасываниях – 0,5005.

 

 

Геометрическое определение вероятности

Еще один недостаток классического определения, ограничивающий его применение, является то, что оно предполагает конечное число возможных исходов. В некоторых случаях этот недостаток можно устранить, используя геометрическое определение вероятности. Пусть, например, плоская фигура  g составляет часть плоской фигуры G (рис.3).

 

Рис.3

 

На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны», в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события А – попадание брошенной точки на g пропорциональна площади этой фигуры S_g и не зависит ни от ее расположения относительно области G, ни от формы g, найдем

 

Р(А) = S_g/S_G

 

где S_G – площадь области G. Но так как области g и G могут быть одномерны-                                                                                                                                                                                                                                   ми, двухмерными, трехмерными и многомерными, то, обозначив меру области через meas, можно дать более общее определение геометрической вероятности 

                                                   

 P = measg / measG.

Доказательство.

 

Р(В/А) = Р(ВÇА)/Р(А) = Р(АÇВ)/Р(А) = {P(a / b)Р(В)}/Р(А) = {Р(А)Р(В)}/Р(А) = Р(В).

Из определения 4 вытекают формулы умножения вероятностей для зависимых и независимых событий.

Следствие 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

 

P(A₁A₂… A_n) = P(A₁)P_A1(A₂)P_A1A2(A₃)… P_{A1A2… An-1}(A_n).

Определение 6. События A _1, A _2, …, A_n независимы в совокупности, если независимы любые два из них и независимы любое из этих событий и любые комбинации (произведения) остальных событий.

Следствие 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

P(A₁A₂… A_n) = P(A₁)P(A₂)… P(A_n).

Доказательство.

P(A₁A₂… A_n) = P(A₁·A₂… A_n) = P(A₁)P(A₂… A_n).=…= P(A₁)P(A₂)… P(A_n).

Определение 7. Событие А₁,А₂,… А _n образуют полную группу событий, если они попарно несовместны (А _i∩А _j = Ø, для любого i ≠ j) и в совокупности образуют Ω, т.е. .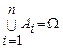 

Теорема 2. Если события А_1, A ₂ ,… А _n образуют полную группу событий, Р(А _i) > 0 (так как не будет определено P(B/A_i)), то вероятность некоторого события B Î S определяется, как сумма произведений безусловных вероятностей наступления события А _i на условные вероятности наступления события B, т.е.

                                         .                                        (1)

Доказательство.  Так как события А _i попарно несовместны, то их пересечение с событием B также попарно несовместны, т.е. B ∩А _i и B ∩А _j – несовместны при i ¹ j . Используя свойство дистрибутивности ((ÈА _i)ÇВ = È(А_iÇВ)), событие B можно представить как 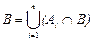. Воспользуемся аксиомой сложения 3 и формулой умножения вероятностей, получим

.

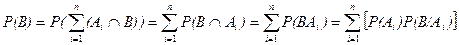Формула (1) называется формула полной вероятности.

Из формулы полной вероятности легко получить формулу Байеса, при дополнительном предположении, что P(B)>0

 

,

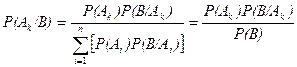где k = 1, 2, …, n.

Доказательство. P (А _k / B ) = P (А _k ∩ B )/ P ( B )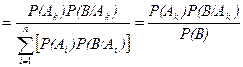

 

Вероятности событий P(А _i ), i =1, 2, …, n называются априорными вероятностями, т.е. вероятностями событий до выполнения опыта, а условные вероятности этих событий P(А _k/B), называются апостериорными вероятностями, т.е. уточненными в результате опыта, исходом которого послужило появление события В.

Задача. В торговую фирму поступили сотовые телефоны последних моделей от трех производителей Alcatel, Siemens, Motorola в соотношении 1 : 4 : 5. Практика показала, что телефоны, поступившие от 1-го, 2-го, 3-го производителя, не потребуют ремонта в течение гарантийного срока соответственно в 98 %, 88 % и 92 % случаев. Найти вероятность того, что поступивший в продажу телефон не потребует ремонта в течение гарантийного срока, проданный телефон потребовал ремонта в течение гарантийного срока, от какого производителя вероятнее всего поступил телефон.

Пример 1.

Очки на гранях игральной кости	1	2	3	4	5	6
Вероятности	1/6	1/6	1/6	1/6	1/6	1/6

Пример 2.

Монета	Орёл	Решка
Вероятность	0,5	0,5

Определение 1. Случайной величиной в ероятностного пространства {Ω, S , P } называется любая функция X(w), определенная для wÎΩ, и такая, что для всех действительных х ( 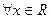) множество {w: X(w) < x }принадлежит полю S . Другими словами для любого такого события w определена вероятность P(X(w) < x) = P(X < x).

Случайные величины будем обозначать прописными латинскими буквами X, Y, Z, …, а значения случайных величин – строчными латинскими буквами x, y, z...

Определение 2. Случайная величина X называется дискретной, если она принимает значения только из некоторого дискретного множества. Другими словами, существует конечное или счетное число значений x₁, x₂, …, таких, что P(X = x_i) = р _i ³ 0, i = 1, 2…, причем  å p_i = 1.

Если известны значения случайной величины и соответствующие им вероятности, то говорят, что определен закон распределения дискретной случайной величины.

Если составлена таблица, в верхней части которой располагаются значения случайных величин, а в нижней части соответствующие им вероятности, то получим ряд распределения случайной величины, который задает закон распределения дискретной случайной величины.

Пример 3. Составим ряд распределения выпадения герба при 2 подбрасываниях монеты. Возможные исходы – ГГ, ГР, РГ, РР. Из возможных исходов видно, что герб может выпасть 0, 1 и 2 раза, с соответствующими вероятностями – ¼, ½, ¼. Тогда ряд распределения примет вид

X_i : 0   1    2

р_i : ¼   ½  ¼

Определение 3. Функцией распределения случайной величины X называется функция F(x), зависящая от х Î R и принимающая значение, равное вероятности события w, что X < x, т.е., F(x) = P{w: X(w) < x } = P(X < x ).

 Из определения следует, что любая случайная величина имеет функцию распределения.

 

Равномерное распределение

Определение 1. Случайная величина Х, принимающая значения 1, 2, …, n , имеет равномерное распределение, если P_m = P(Х = m) = 1/n,

m = 1, …, n .

Очевидно, что .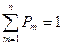

 

Рассмотрим следующую задачу. В урне имеется N шаров, из них M шаров белого цвета. Наудачу извлекается n шаров. Найти вероятность того, что среди извлечённых будет m белых шаров.

Нетрудно видеть, что .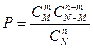

 

Распределение Пуассона

Определение 4. Случайная величина Х имеет распределение Пуассона с параметром l, если 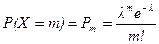, m = 0, 1, …

Покажем, что Σp_m = 1. .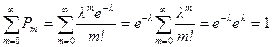

 

Биномиальное распределение

 Определение 5. Случайная величина X имеет биномиальное распределение, если 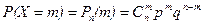, m = 0, 1, …, n,

где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1– p.

Распределение Бернулли

 Определение 6. Случайная величина Х имеет распределение Бернулли, если P(Х = m) = P_m = p^mq^{n - m}, m = 0, 1, …, n.

При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то .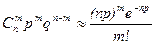

Теорема Пуассона. Если n ® ¥, а p ® 0, так что np ® l, то .

Доказательство. Обозначим l_n = np, по условию теоремы 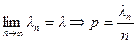, тогда

.

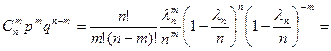
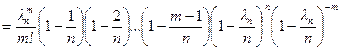При n ® ¥, l_n ^m ® l^m,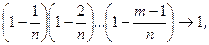            

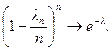
Отсюда получаем утверждение теоремы. Р _n(m) ® 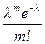 при n ® ¥.

Формула Пуассона хорошо приближает формулу Бернулли, если npq £ 9. Если же произведение npq велико, то для вычисления Р _n ( m ) используют локальную теорему Муавра–Лапласа.

Локальная теорема Муавра – Лапласа. Пусть pÎ(0;1) постоянно, величина  равномерно ограничена, т.е. $с, | x_m |<с. Тогда

,

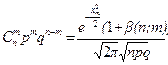где b ( n ; m ) – бесконечно малая величина, причем .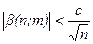

Из условий теоремы следует, что ,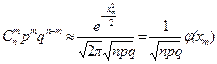                             

где , .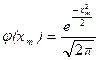

Для вычисления Р _n ( m ) по формуле, приведенной рнее, используют таблицы функции

.

 

Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.

 

Решение .

xi	0	1	2	3
рi	0,343	0,441	0,189	0,027

 

Задача 2. Вероятность поломки произвольного компьютера равна 0,01. Построить ряд распределения числа вышедших из строя компьютеров с общим числом 25.

 

Решение .

xi	0	1	2	3	4	5	6	…	25
рi  (Пуассон)	0,778	0,196	0,024	0,002	0,000	0,000	0,000	0,000	0,000
рi  (Бернулли)	0,779	0,195	0,022	0,001	0,000	0,000	0,000	0,000	0,000

 

Задача 3. Автомобили поступают в торговый салон партиями по 10 шт. В салоне подвергаются контролю качества и безопасности только 5 из 10 поступивших автомобилей. Обычно 2 из 10 поступивших машин не удовлетворяют стандартам качества и безопасности. Чему равна вероятность, что хотя бы одна из 5 проверяемых машин будет забракована.

Решение. Р = Р₍₁₎ + Р₍₂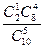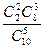₎ =  + =0,5556 + 0,2222 = 0,7778

 

Доказательство.

 

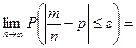
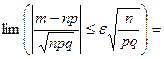
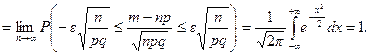
Задача 1. Вероятность того, что случайно выбранный прибор нуждается в дополнительной настройке, равна 0,05. Если при выборочной проверке партии приборов обнаруживается, что не менее 6 % отобранных приборов нуждаются в регулировке, то вся партия возвращается для доработки. Определить вероятность того, что партия будет возвращена, если для контроля из партии выбрано 500 приборов.

Решение . Партия будет возвращена, если число отобранных приборов, нуждающихся в настройке, будет больше 6%, т.е. m₁ = 500 × 6/100 = 30. Далее: p = 0,05: q = 0,95; np = 25; 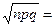4,87. За успех считаем, если прибор требует дополнительной настройки.

Применим интегральную теорему Муавра–Лапласа.

 

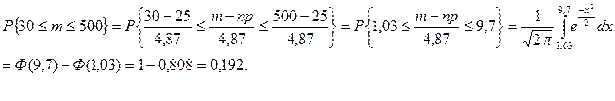
Задача 2. Определить, сколько надо отобрать изделий, чтобы с вероятностью 0,95 можно было утверждать, что относительная частота бракованных изделий будет отличаться от вероятности их появления не более чем на 0,01.

Решение . Для решения задачи выберем в качестве математической модели схему Бернулли и воспользуемся формулой (4). Надо найти такое n, чтобы выполнялось равенство (4), если e = 0,01, b = 0,95, вероятность р неизвестна.

Ф(х_b)  = (1 + 0,95) / 2 = 0,975. По таблице приложения найдем, что х_b = 1,96. Тогда по формуле (4) найдем n = ¼ × 1,96²/0,01² = 9600.

 

Равномерное распределение

Определение 5. Непрерывная случайная величина Х, принимающая значение на отрезке [ a , b ], имеет равномерное распределение, если плотность распределения имеет вид

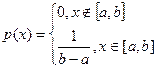                                            .                                        (1)

Нетрудно убедиться, что ,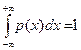

.

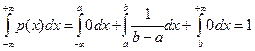Если случайная величина равномерно распределена, то вероятность того, что она примет значение из заданного интервала [x; x+∆] не зависит от положения интервала на числовой прямой и пропорциональна длине этого интервала

^.

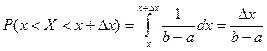Покажем, что функция распределения Х имеет вид

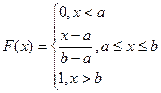                                     .                                           (2)

Пусть хÎ (–¥,a), тогда F(x) = .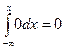

Пусть хÎ [a,b], тогда F(x) = .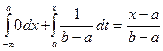

Пусть х Î (b,+¥], тогда F(x) = 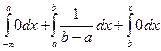 = 0 + .

Найдем медиану x_0,5. Имеем F(x_0,5) = 0,5, следовательно

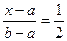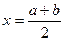, . Итак, медиана равномерного распределения совпадает с серединой отрезка [a, b]. На рис.1 приведен график плотности р(х) и функции распределения F(x)

для равномерного распределения.

 

Рис. 1

Нормальное распределение

 

Определение 7. Непрерывная случайная величина имеет нормальное распределение, с двумя параметрами a, s , если

                             , s>0.                                        (5)

 

Тот факт, что случайная величина имеет нормальное распределение, будем кратко записывать в виде Х ~ N(a;s).

Покажем, что p(x) – плотность

 

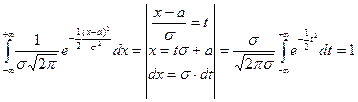(показано в лекции 6).

 

График плотности нормального распределения (рис. 3) называют нормальной кривой (кривой Гаусса).

     

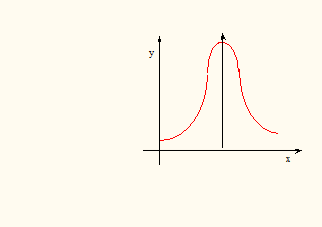
Рис.3

 

Плотность распределения симметрична относительно прямой х = a. Если х ® ¥, то р(х) ® 0. При уменьшении s график «стягивается» к оси симметрии х = a.

Нормальное распределение играет особую роль в теории вероятностей и ее приложениях. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет «примерно» нормальное распределение.

Так как 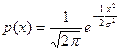 – плотность нормального закона распределения с параметрами а = 0 и s =1, то функция  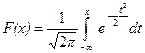= Ф(х), с помощью которой вычисляется вероятность 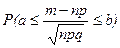, является функцией распределения нормального распределения с параметрами а = 0 и s =1.

Функцию распределения случайной величины Х с произвольными параметрами а, s можно выразить через Ф(х) – функцию распределения нормальной случайной величины с параметрами а = 0 и s =1. 

Пусть Х ~ N(a;s), тогда

 

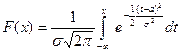                                 .                                        (6)

 

Сделаем замену переменных под знаком интеграла , получим

=

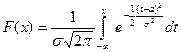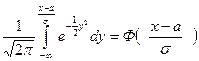
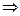
                                      F(x) = .                                                 (7)

В практических приложениях теории вероятностей часто требуется найти вероятность того, что случайная величина примет значение из заданного отрезка 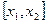. В соответствии с формулой (7) эту вероятность можно найти по табличным значениям функции Лапласа

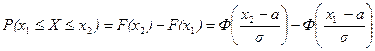                    .                (8)             

Найдем медиану нормальной случайной величины Х ~ N(a;s). Так как плотность распределения р(х) симметрична относительно оси х = а, то

 

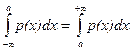
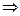
                                      р(х < a) = p(x > a) = 0,5.               

 

Следовательно, медиана нормальной случайной величины совпадает с параметром а:

Х_0,5 = а.

 

Задача 1. Поезда в метро идут с интервалом в 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Х, в течение которого ему придется ждать поезд, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0, 2) мин. Найти вероятность того, что пассажиру придется ждать ближайший поезд не более 0,5 мин.

Решение. Очевидно, что p ( x ) = 1/2. Тогда, Р_0,5 = Р(1,5< X <2) = 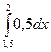= 0,25

Задача 2. Волжский автомобильный завод запускает в производство новый двигатель. Предполагается, что средняя длина пробега автомобиля с новым двигателем – 160 тыс. км, со стандартным отклонением – σ = 30 тыс.км. Чему равна вероятность, что до первого ремонта число км. пробега автомобиля будет находиться в пределах от 100 тыс. км. до 180 тыс. км.

 

Решение . Р(100000< X < 180000) = 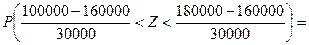 Ф(2/3)–Ф(–2) = 0,2454 + 0,4772 = 0,7226.

 

Свойства дисперсии

1. Дисперсия постоянной C равна 0,  DC = 0, С = const.

Доказательство. DC = M(С – MC)² = М(С – С) = 0.

 

2. D(CX) = С²DX.

Доказательство. D(CX) = M(CX)² – M²(CX) = C²MX² – C²(MX)² = C²(MX² – M²X) = С²DX.

 

3. Если X и Y – независимые случайные величины, то

 

Доказательство.

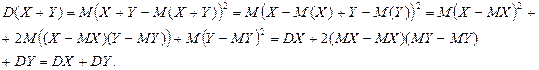
4. Если Х₁, Х₂, … не зависимы, то .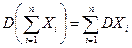

Это свойство можно доказать методом индукции, используя свойство 3.

 

5. .

Доказательство. D(X – Y) = DX + D(–Y) = DX + (–1)²D(Y) = DX + D(Y).

 

6.

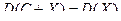
Доказательство. D ( C + X ) = M ( X + C – M ( X + C ))² = M ( X + C – MX – MC )² = M ( X + C – MX – C )² = M ( X – MX )² = DX .

Пусть 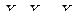 – независимые случайные величины, причем , .

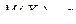Составим новую случайную величину 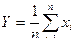, найдем математическое ожидание и дисперсию Y.

; .

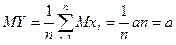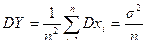
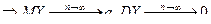То есть при n®¥ математическое ожидание среднего арифметического n независимых одинаково распределенных случайных величин остается неизменным, равным математическому ожиданию а, в то время как дисперсия стремится к нулю.

Это свойство статистической устойчивости среднего арифметического лежит в основе закона больших чисел.

 

Нормальное распределение

Пусть X имеет нормальное распределение. Раннее, в лекции 11 (пример 2) было показано, что если

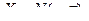
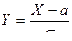, то Y ~ N(0,1).

Отсюда 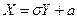, и тогда , поэтому найдем сначала DY.

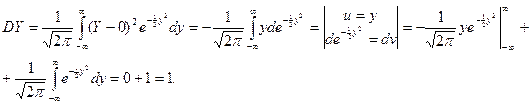
Следовательно       

DX = D(sY+a) = s²DY = s², s_x = s.                                (2)

 

Распределение Пуассона

 

Как известно                

Ранее мы показали, что , воспользуемся формулой .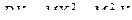

 

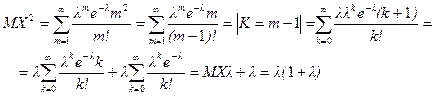
Следовательно,

                                          (4)

 

Равномерное распределение

Известно, что .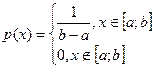

Ранее мы показали, что , воспользуемся формулой .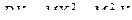

,

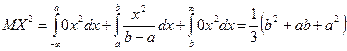тогда

.                       (5)

Доказательство.

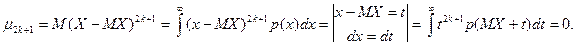
Последний интеграл в цепочке равенств равен 0, так как из условия задачи следует, что p ( MX + t ) – четная функция относительно t (p ( MX + t ) = p ( MX - t )), а t ^{2 k +1} – нечетная функция. 

Так как плотности нормального и равномерного законов распределений симметричны относительно х = МХ, то все центральные моменты нечетного порядка равны 0.

Теорема 2. Если X~N(a,s), то .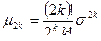

Чем больше моментов случайной величины известно, тем более детальное представление о законе распределения мы имеем. В теории вероятностей и математической статистике наиболее часто используются две числовые характеристики, основанные на центральных моментах 3-го и 4-го порядков. Это коэффициент асимметрии и эксцесс случайной величины.

Определение 3. Коэффициентом асимметрии случайной величины Х называется число b = .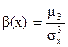

Коэффициент асимметрии является центральным и начальным моментом нормированной случайной величины Y, где 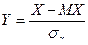. Справедливость этого утверждения следует из следующих соотношений:

.

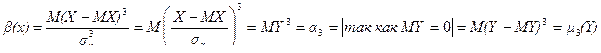Асимметрия случайной величины Х равна асимметрии случайной величины Y = αХ + β

c точностью до знака α, 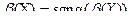. Это следует из того, что нормирование случайных величин aХ+ b и Х приводит к одной и той же случайной величине Y с точностью до знака

 

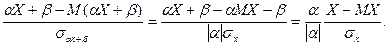
Если распределение вероятностей несимметрично, причем «длинная часть» графика расположена справа от центра группирования, то β(х) > 0; если же «длинная часть» графика расположена слева, то β(х) < 0. Для нормального и равномерного распределений β = 0.

В качестве характеристики большей или меньшей степени «сглаженности» кривой плотности или многоугольника распределения по сравнению с нормальной плотностью используется понятие эксцесса.

Определение 4. Эксцессом случайной величины Х называется величина

g = .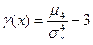

Эксцесс случайной величины Х равен разности начального и центрального моментов 4-го порядка нормированной случайной величины  и числа  3, т.е. . Покажем это:

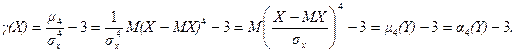
Эксцесс случайной величины Х равен эксцессу случайной величины

 

Y = αХ + β.

 

Найдем эксцесс нормальной случайной величины Х.

Если Х~N(a,s), то 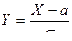 ~  (0,1).

Тогда

 

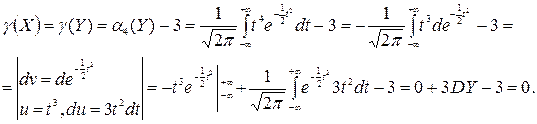
Таким образом, эксцесс нормально распределенной случайной величины равен 0. Если плотность распределения одномодальна и более «островершинна», чем плотность нормального распределения с той же дисперсией, то g(Х) > 0, если при тех же условиях менее «островершинна», то g(Х) < 0.

Закон больших чисел

Закон больших чисел устанавливает условия сходимости среднего арифметического случайных величин к среднему арифметическому математических ожиданий.

Определение 1. Последовательность случайных величин  называется сходящейся по вероятности p к числу b, если

 

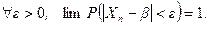
Сходимость по вероятности коротко обозначают так: .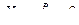

 

Теорема 2. (Закон больших чисел в форме Чебышева) Пусть 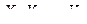 – последовательность независимых случайных величин, дисперсии которых равномерно ограничены сверху, т.е. 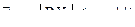; математические ожидания конечны, тогда

.

Доказательство. Так как DX_i £ c, i = 1, 2, …, n, то 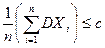. Используя формулу (5) (следствие 2), имеем

 

.

 

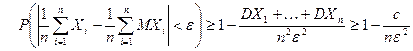 Так как вероятность любого события не превышает единицы, получим двойное неравенство

.

 

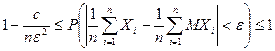 Перейдем в этом неравенстве к пределу при 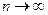и получим

 .

 

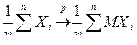Интервальная оценка

Если получена точечная оценка неизвестного параметра по выборке, то говорить о полученной оценке как об истинном параметре довольно рискованно. В некоторых случаях, целесообразнее, получив разброс оценки параметра, говорить об интервальной оценке истинного значения параметра. В качестве иллюстрации сказанного рассмотрим построение доверительного интервала для математического ожидания нормального распределения.

Мы показали, что – наилучшая оценка (абсолютно корректная) для математического ожидания МХ = Q, поэтому  является абсолютно корректной оценкой также и для параметра a = 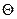нормального распределения

                   

по выборке объема n. Предположим, что задана выборка Х _i, i= . Дисперсия генеральной совокупности известна и равна s². Как далеко может находиться случайная величина от неизвестного математического ожидания Q, оценкой которого она является? Чтобы ответить на этот вопрос, рассмотрим случайную величину , представляющую отклонение от Q. Отклонение D может изменяться от 0 до +¥, но нас интересует, прежде всего, вероятность того, что отклонение D не превысит предельной ошибки e допустимого уровня

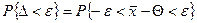                 .                                    (8)

В формуле (8) только величина является случайной, поэтому вероятность Р зависит только от распределения .

Очевидно, что события A = {–e<Q– <e} и B = {–e+ <Q<e+ } эквивалентны, так как если произойдет событие А, то произойдет и событие В и наоборот. Поэтому

                            Р{–e+Q< <e+Q} = Р{–e+ <Q<e+ }.                       (9)

Таким образом, если – функция распределения непрерывной, случайной величины , то                          

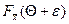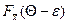                 Р{–e+Q< <e+Q}= –                        (10)

Определим функцию распределения 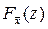 случайной величины , где х _i Î N(q,s²). Известно, что линейная функция от нормальных случайных величин является нормальной. Поэтому – нормальная, а нормальная случайная величина задается двумя параметрами – математическим ожиданием и дисперсией, но

.

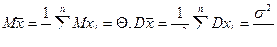Таким образом, плотность распределения имеет вид

.

 

Поэтому Р{-e+Q< <e+Q}= .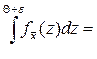

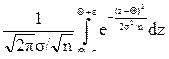В полученном интеграле произведем замену переменных u= 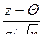, получим

Р{-e+Q< <e+Q}=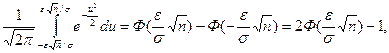

где Ф(z) – функция распределения нормированной нормальной случайной величины.

Таким образом, 

Р{-e+ <Q<e+ }= 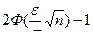.                                    (11)

 

Если обозначить -e+ = Q₁, e+ = Q₂, то получим интервал (Q_1, Q₂), который накрывает с вероятностью, равной 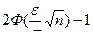, неизвестную величину Q и эта вероятность не зависит от Q, т.е., она одна и та же для любых значений Q. Чтобы найти сам интервал, надо по выборке вычислить  и задать e.

Можно по заданной вероятности Р найти концы интервала. Для этого надо воспользоваться формулой 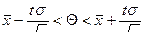, где t – значение аргумента функции Лапласа, при котором Ф(t ) = 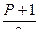, e = .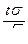

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ

 

1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и мате-

матическая статистика. М.: Высшая Школа, 1991.

2. Елисеева И.И., Князевский В.С., Ниворожкина Л.И., Морозова З.А. Теория статистики с основами теории вероятностей. М.: Юнити, 2001.

3. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.: Мир, 1990.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2001

5. Смирнов Н.В. Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука,1969.

6. Статистические методы построения эмпирических формул. М.: Высшая Школа, 1988.

 

 

ОГЛАВЛЕНИЕ

 

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 3

ЛЕКЦИЯ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. СТАТИСТИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 8

ЛЕКЦИЯ 3. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АКСИОМАТИКА КОЛМОГОРОВА.. 14

ЛЕКЦИЯ 4. СЛУЧАЙНАЯ ВЕЛИЧИНА. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.. 17

ЛЕКЦИЯ 5. РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 21

ЛЕКЦИЯ 6. ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА–ЛАПЛАСА, ТЕОРЕМА БЕРНУЛЛИ.. 26

ЛЕКЦИЯ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 29

ЛЕКЦИЯ 8. ПОНЯТИЕ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 35

ЛЕКЦИЯ 9. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 39

ЛЕКЦИЯ 10. СВОЙСТВА ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 43

ЛЕКЦИЯ 11. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН.. 48

ЛЕКЦИЯ 12. ТЕОРЕМА О ПЛОТНОСТИ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 52

ЛЕКЦИЯ 13. РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА, ФИШЕРА .ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.. 57

ЛЕКЦИЯ 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН (продолжение) 61

\ЛЕКЦИЯ 15. ВЫЧИСЛЕНИЕ ДИСПЕРСИИ ОСНОВНЫХ РАСПРЕДЕЛЕНИЙ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.. 67

ЛЕКЦИЯ 16. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МЕРЫ СВЯЗИ СЛУЧАЙНЫХ ВЕЛИЧИН.. 71

ЛЕКЦИЯ 17. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. НЕРАВЕНСТВО ЧЕБЫШЕВА. ЗАКОН БОЛЬШИХ ЧИСЕЛ.. 76

ЛЕКЦИЯ 18. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА.. 79

ЛЕКЦИЯ 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ВАРИАЦИОННЫЕ РЯДЫ... 82

ЛЕКЦИЯ 20. СРЕДНИЕ ВЕЛИЧИНЫ. ПОКАЗАТЕЛИ ВАРИАЦИИ.. 87

ЛЕКЦИЯ 21. ОЦЕНКА ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ.. 93

ЛЕКЦИЯ 22. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ 97

ЛЕКЦИЯ 23. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. 104

ЛЕКЦИЯ 24. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ.. 107

ЛЕКЦИЯ 25. ЭЛЕМЕНТЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ.. 114

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ.. 122

 

А.А. Халафян

 

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

 

тексты лекций

 

 

Краснодар 2008

 

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

 

Принципиально невозможно говорить об абсолютно одинаковых реальных объектах окружающего нас мира и абсолютно одинаковых воздействиях на них, а потому и об абсолютной детерминированности. Все реальные объекты и явления имеют, по-видимому,  черты как детерминированного, так и случайного, которые могут проявляться в большей или меньшей степени, поэтому вопрос, а каким является мир на самом деле, в принципе не допускает однозначного ответа.

Например, на основании законов небесной механики по известному в настоящем положению планет Солнечной системы может быть практически однозначно предсказано их положение в любой наперед заданный момент времени, в том числе очень точно могут быть предсказаны солнечные и лунные затмения. Это пример детерминированных законов [1]. Но не все явления окружающего нас мира поддаются точному предсказанию, несмотря на то, что наши знания о нем постоянно углубляются и расширяются. Например, долговременные изменения климата, кратковременные изменения погоды, землетрясения и другие природные катаклизмы не являются объектами для успешного прогнозирования.

Еще менее детерминированными являются некоторые законы и явления микромира. Например, нельзя говорить о точном положении электрона в определенный момент времени, но можно лишь говорить о его распределенном положении в пространстве (электронное облако). Такого рода законы называются статистическими. Согласно этим законам, будущее состояние системы определяется не однозначно, а лишь с некоторой вероятностью [1].

Но в макромире и микромире существуют явления, состояние которых в перспективе предсказать невозможно даже с определенной вероятностью. Такие явления можно назвать неопределенными, например, длительность боевых действий при вооруженных конфликтах, количество погибших, число разрушений и т.д.

Теория вероятностей изучает свойства массовых случайных событий, способных многократно повторяться при воспроизведении определенного комплекса условий. Основное свойство любого случайного события, независимо от его природы, – мера или вероятность его осуществления.

Теория вероятностей – математическая наука. Из первоначально заданной системы аксиом вытекают другие ее положения и теоремы. Впервые законченную систему аксиом сформулировал в 1936 г. советский математик академик А.Н. Колмогоров в своей книге «основные понятия теории вероятностей» [1].

По аналогии с макромиром и микромиром, математические модели могут либо быть детерминированными, либо включать случайные факторы. Если эти факторы являются стохастическими, т.е. подчиняются с определенной точностью законам математической статистики, то говорят о стохастических математических моделях.

Так как большинство прикладных задач являются вероятностными по самой своей природе, за последние годы стохастические модели получили широкое распространение. К тому же в некоторых случаях, хотя задача допускает детерминистскую модель, привлечение случайных компонент приводит к более адекватному или к более детальному описанию реального объекта. Например, случайное воздействие иногда можно полностью игнорировать (если оно не слишком велико), в других случаях его можно учесть максимально возможным значением или принять для него какую-либо детерминированную схему, но наиболее естественно так и считать это воздействие случайным, т.е. принять для его описания стохастическую модель. Наконец, случайные компоненты могут быть искусственно введены в чисто детерминированную модель из-за преимуществ при решении математической задачи, например, при вычислении интегралов по области сложной формы и высокой размерности по методу Монте–Карло [2].

Слабым звеном при использовании стохастических моделей является выбор статистических гипотез о вероятностных характеристиках входных случайных величин и функций. Такие характеристики часто считаются либо полностью известными (например, принимается, что исходная величина распределена по нормальному закону с известными параметрами), либо доступными определению. Однако в реальных ситуациях чаще всего оказывается, что нужная информация отсутствует; более того, во многих случаях ситуация является не стохастической, а неопределенной.

Тем не менее, одна из основных тенденций современной математики и ее приложений состоит в резком повышении роли тех разделов науки, которые анализируют явления, имеющие случайный характер, и основываются на теории вероятностей. И всего лишь небольшим преувеличением прозвучала шутка американского математика Дж. Дуба, начавшего свой доклад в Московском математическом обществе словами: «Всем специалистам по теории вероятностей хорошо известно, что математика представляет собой часть теории вероятностей». Эта тенденция объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, оказались тесно связанными с теорией вероятностей. При этом возникновение ряда новых, в большинстве своем «порожденных» теорией вероятностей, наук (например, теория игр, теория информации) привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [2].

Математическая статистика разрабатывает математический аппарат установления статистических закономерностей и получения научно обоснованных выводов о массовых явлениях из данных наблюдений или экспериментов.

С учетом сказанного можно определить теорию вероятностей и математическую статистику как математическую науку, выясняющую закономерности, которые появляются при взаимодействии большого числа случайных факторов.

Теория вероятностей вначале развивалась как прикладная дисциплина. По-видимому, будет верным утверждение, что теория вероятности обязана своему появлению азартным играм. Хотя сегодня теория вероятностей с азартными играми имеет столько же общего как геометрия с измерением площадей. Игра в кости была самой популярной азартной игрой до конца Средних веков. Слово «азарт» происходи от арабского слова «alzar», переводимого как «игральная кость». Согласно греческой легенде, игру в кости предложил Паламедей для развлечения греческих солдат, скучающих при ожидании битвы при Трое (V в. век до н. э.).

Возможно, игра в кости была известна значительно раньше. Так Дж. Нейман в своей книге «Вводный курс теории вероятностей и математической статистики» пишет, что археологи обнаружили в гробнице фараона две пары костей: «честные» (с равными вероятностями выпадения всех граней) и фальшивые (с умышленным смещением центра тяжести, что увеличивало вероятность выпадения шестерок).

Карточные игры появились в Европе лишь в XIV в., в то время как игра в кости пользовалась успехом еще в Древнем Египте во времена 1-й династии, позднее в Греции и Римской империи. 

Самой ранней книгой по теории вероятностей является «Книга об игре в кости» Джордано Кардано (1501–1576). Эта книга была опубликована лишь в 1663 г., спустя 100 лет после написания. Аналогичный трактат был написан Галилеем между 1613 и 1624 г.

Ключевыми моментами развития теории вероятностей были парадоксы, возникающие при попытках моделирования азартных игр. Рассмотрим некоторые из них [3].

Парадокс 1. Игральная кость при бросании с равной вероятностью падает на любую из граней 1, 2, 3, 4, 5, 6. Когда бросают две кости, сумма выпавших очков заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2, 3, 4, 5, 6 можно получить двумя различными способами:

9 = 4 + 5 = 6 + 3;

10 = 5 + 5 = 4 + 6.

В задаче с тремя костями 9 и 10 получаются шестью способами.

Почему тогда 9 появляется чаще, когда бросают две кости, а 10 – чаще, когда бросают три кости. Несмотря на простоту задачи, некоторым великим математикам не удавалось ее решить, так как они забывали о необходимости учета порядка выпадения костей. Ошибались и Лейбниц и Даламбер.

Парадокс 2. Однажды Даламберу задали вопрос: с какой вероятностью монета, брошенная дважды, по крайней мере один раз выпадет гербом вверх. Ответ ученого был 2/3. Ошибкой Даламбера было то, что он рассматривал три возможных исхода (ГР, РР, ГГ) вместо четырех (ГР, РГ, РР, ГГ).

Парадокс 3. Задача шевалье де Мере. Одновременно подбрасываются две кости. Какова вероятность того, что в двадцати четырех подбрасываниях две шестерки выпадут, по крайней мере, 1 раз. По его подсчетам эта вероятность больше 1/2. Но, играя длительное время, он почему-то проигрывал. Шевалье обратился за помощью к Блезу Паскалю, который решил ее и показал, что эта вероятность равна 0,49. Эта задача была также решена Пьером Ферма. Дата опубликования Паскалем решения этой задачи (1654 г.) считается днем рождения науки «Теория вероятностей».