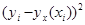По первоначальным динамическим рядам xi, yi с количеством членов n строим новые динамические ряды ui, wi с количеством членов n-1(табл.3.2.1), где:
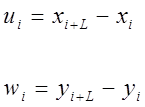 |
Таблица 3.2.1
| ui | wi |
| 640 | 224 |
| 336 | -164 |
| 164 | -276 |
| -144 | -530 |
| -316 | -410 |
| -530 | -396 |
| -450 | -44 |
| -396 | 104 |
| -84 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 336 |
| 550 | 224 |
| 336 | -164 |
| 184 | -276 |
| -164 | -530 |
| -316 | -470 |
| -530 | -336 |
| -450 | -44 |
| -316 | 104 |
| -164 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 366 |
Далее считаем автокорреляцию для динамических рядов u и w:
Для динамического ряда ui:
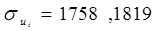 | |||
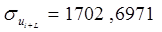 | |||
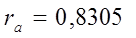 | |||
Для динамического ряда wi:
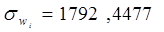 |
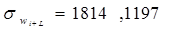
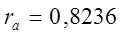 |
Т.к. полученные коэффициенты корреляции больше табличного, то переходим к следующему методу.
3.3.Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования остатков (отклонений от трендов)
В данном случае зависимость ищется в виде eyi=f(exi), где:
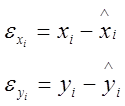 | |||||
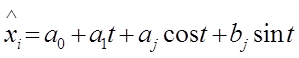 | |||||
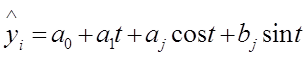 | |||||
Значения 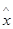 и
и 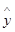 представлены в табл.3.3.1:
представлены в табл.3.3.1:
Таблица 3.3.1
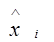 | 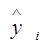 | ||
|
|
| |
3642,182105 | 5521,14579 | |
| 4045,276912 | 5549,19234 | |
| 4270,521342 | 5237,823029 | |
| 4251,468517 | 4673,817411 | |
| 3987,065165 | 4011,580844 | |
| 3541,933559 | 3431,813196 | |
| 3029,073401 | 3093,139015 | |
| 2579,614001 | 3089,646833 | |
| 2307,713526 | 3425,703505 | |
| 2280,001083 | 4014,785285 | |
| 2497,741411 | 4702,638546 | |
| 2896,496334 | 5308,570463 | |
| 3363,373599 | 5673,816955 | |
| 3767,245937 | 5704,040732 | |
| 3993,851263 | 5394,583544 | |
| 3976,378415 | 4831,713105 | |
| 3713,351191 | 4169,53091 | |
| 3269,023502 | 3588,722272 | |
| 2756,179857 | 3248,190391 | |
| 2305,945146 | 3242,52107 | |
| 2032,68507 | 3576,663941 | |
| 2003,392677 | 4164,607546 | |
| 2219,755627 | 4852,402924 | |
| 2617,70444 | 5459,372744 | |
| 3084,562645 | 5826,4751 |
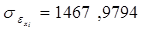 Для признака xi:
Для признака xi:
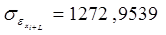 | |||
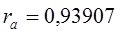 | |||
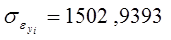 Для признака yi:
Для признака yi:
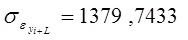 | |||
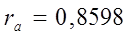 | |||
Т.к. полученные коэффициенты корреляции опять больше табличного, то переходим к следующему методу.
Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования с учётом фактора времени
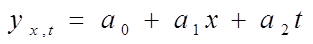 Для более удобного расчёта изменяем масштаб времени, т.е. Dt =1. Простейшее уравнение регрессии имеет вид:
Для более удобного расчёта изменяем масштаб времени, т.е. Dt =1. Простейшее уравнение регрессии имеет вид:
Тогда система уравнений, полученная методом наименьших квадратов имеет следующий вид:
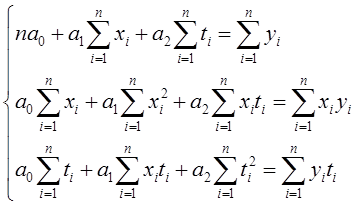
Необходимо отметить, что в этом методе коэффициент автокорреляции не исследуется.
Решение системы уравнений методом Гаусса, все необходимые данные в табл.3.4.1:
Таблица 3.4.1
| t | x2 | xt | yx | t2 | yt |
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 8410000 | 2900 | 14111400 | 1 | 4866 | 710092,7896 | |
| 2 | 12531600 | 7080 | 18018600 | 4 | 10180 | 534945,7467 | |
| 3 | 15023376 | 11628 | 19093176 | 9 | 14778 | 144386,4657 | |
| 4 | 16321600 | 16160 | 18786000 | 16 | 18600 | 0,047492264 | |
| 5 | 15178816 | 19480 | 16051520 | 25 | 20600 | 234012,5049 | |
| 6 | 12816400 | 21480 | 13281800 | 36 | 22260 | 583789,6833 | |
| 7 | 9302500 | 21350 | 10107700 | 49 | 23198 | 858020,2697 | |
| 8 | 6760000 | 20800 | 8502000 | 64 | 26160 | 601299,3152 | |
| 9 | 4857616 | 19836 | 7436296 | 81 | 30366 | 252847,3424 | |
| 10 | 4494400 | 21200 | 8119600 | 100 | 38300 | 899,2211526 | |
| 11 | 4946176 | 24464 | 9563200 | 121 | 47300 | 133539,1856 | |
| 12 | 6969600 | 31680 | 12909600 | 144 | 58680 | 531592,5221 | |
| 13 | 9672100 | 40430 | 16252860 | 169 | 67938 | 660179,6832 | |
| 14 | 13395600 | 51240 | 19947000 | 196 | 76300 | 555049,3853 | |
| 15 | 15968016 | 59940 | 21122856 | 225 | 79290 | 154919,9389 | |
| 16 | 17472400 | 66880 | 20941800 | 256 | 80160 | 16,86990836 | |
| 17 | 16128256 | 68272 | 17991680 | 289 | 76160 | 221023,9832 | |
| 18 | 13690000 | 66600 | 14837000 | 324 | 72180 | 656820,769 | |
| 19 | 10048900 | 60230 | 11646580 | 361 | 69806 | 832979,8976 | |
| 20 | 7398400 | 54400 | 9873600 | 400 | 72600 | 580367,2874 | |
| 21 | 5779216 | 50484 | 8976536 | 441 | 78414 | 278922,6984 | |
| 22 | 5017600 | 49280 | 9385600 | 484 | 92180 | 267,9934274 | |
| 23 | 5494336 | 53912 | 10923040 | 529 | 107180 | 143676,3624 | |
| 24 | 7617600 | 66240 | 14490000 | 576 | 126000 | 551633,6354 | |
| 25 | 10432900 | 80750 | 18139680 | 625 | 140400 | 732960,1726 | |
| Сумма | 325 | 255727408 | 986716 | 350509124 | 5525 | 1453896 | 9954243,77 |
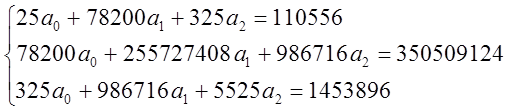 | |||||||
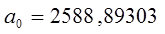 | |||||||
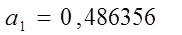 | |||||||
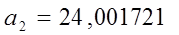 | |||||||
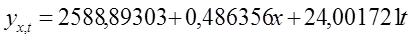

Далее определяем индекс корреляции:
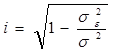 | |||
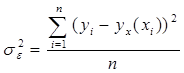 | |||
где yx(xi) – значение величины y, рассчитанное по уравнению регрессии при подстановке в него значений xi и ti; yi – значения y из исходной таблицы.
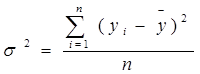 | |||||||
 | |||||||
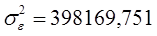 | |||||||
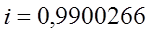 | |||||||
Значимость индекса корреляции определяем с помощью критерия Фишера, фактическое значение критерия Фишера равно:
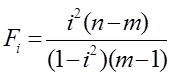 | |||
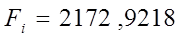 | |||
Табличное значение критерия Фишера определяем по табл.5 приложения, задаваясь уравнением значимости a и числом степеней свободы k1=m-1; k2=n-m.
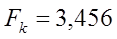 | |||
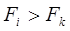 | |||
Если то величину индекса корреляции считаем значимой.
Определим коэффициент детерминации:
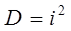 | |||
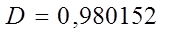 | |||
Следовательно, величина y зависит от величин x и t на 98,01%. Остальные 1,99% - это зависимость величины y от неучтённых величин.
Подводя итог необходимо отметить, что в исследовании методом коррелирования динамических рядов, с учётом фактора времени была определена весьма высокая теснота связи, равная 0,9900; величина коэффициента детерминации равная 0,9801 говорит о том, что величина y зависит от величин x и t, включённых в уравнение, на 98,01%, все остальные 1,99% - это зависимость величины y от неучтённых величин.
Дата: 2019-04-23, просмотров: 294.