Этот и последующие этапы работы в этом разделе выполняем для каждого изучаемого признака в отдельности.
 |
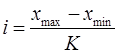Принимая во внимание, что выборочная совокупность содержит n значений, величину равных интервалов выбираем по формуле Г.А. Стерджесса:
где К = 1+3,322gn- число интервалов; при n=30 К=5. xmax и xmin - минимальное и максимальное значения признака.
Определяем границы интервалов. Для первого интервала левая граница равна xmin, а правая – xmin +i и, для второго, соответственно - xmin +i и xmin +2i и т.д.
Строим таблицу частоты распределения значений признака по интервалам и гистограмму. Для определенности считаем, что значение признака, лежащее на границе двух интервалов, попадает в правый интервал.
Для показателя x: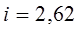 
Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:
| Границы интервалов | Число предприятий | |
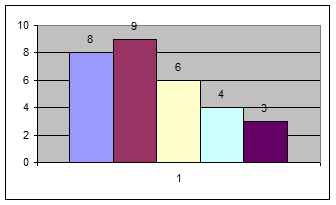
| 31,4 | 34,02 | 8 |
| 34,02 | 36,64 | 9 |
| 36,64 | 39,26 | 6 |
| 39,26 | 41,88 | 4 |
| 41,88 | 44,5 | 3 |
Строим гистограмму:
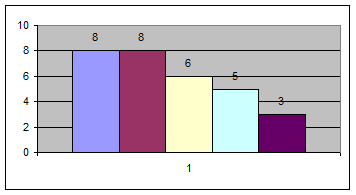
Для показателя y: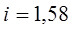 
Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:
| Границы интервалов | Число предприятий | |
| 30,5 | 32,08 | 8 |
| 32,08 | 33,66 | 8 |
| 33,66 | 35,24 | 6 |
| 35,24 | 36,82 | 5 |
| 36,82 | 38,4 | 3 |
Строим гистограмму:
3. Проверка соответствия эмпирического распределения нормальному закону распределения
Для проверки соответствия эмпирического распределения случайной величины нормальному закону распределения в нашем случае (при n<30) можно использовать критерии Шапиро-Уилкса (W) и Колмогорова (D). В нашем случае мы используем критерий Колмогорова.
 |
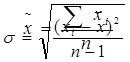Сначала определим среднюю величину
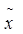и среднее квадратическое отключение от нее, считая выборку малой:
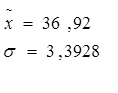Для признака x:
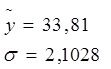Для признака y:
Вычисляем ошибку определения средней по выборочной совокупности (ошибку выборки):
 |
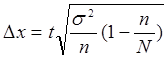где n - численность выборки; N= 100 - численность генеральной совокупности; t - коэффициент доверия; при доверительной вероятности 95,45% t=2.
 |
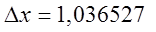Для признака x:
 |
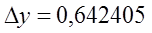Для признака y:
Генеральная средняя располагается в следующих границах:
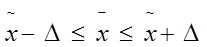
Определяем эти границы:
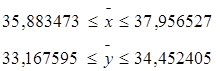
Ранжируем значения величин x и y по возрастанию (табл.1.2.):
x1£ x2 < …£ xn-1£ xn
Таблица 1.2.
| X | Y |
| 1 | 2 |
| 31,4 | 30,5 |
| 32,5 | 30,7 |
| 32,7 | 31,4 |
| 32,8 | 31,3 |
| 33,2 | 31,6 |
| 33,3 | 31,4 |
| 33,7 | 32 |
| 33,7 | 31,9 |
| 34,9 | 32,6 |
| 35,4 | 32,9 |
| 35,7 | 33,2 |
| 35,8 | 32,8 |
| 35,9 | 32,6 |
| 36,2 | 33,7 |
| 36,2 | 33,5 |
| 36,3 | 33,6 |
| 36,6 | 33,7 |
| 37,1 | 33,5 |
| 37,8 | 34,3 |
| 38,4 | 34,6 |
| 38,8 | 35,1 |
| 38,8 | 35 |
| 38,9 | 35,3 |
| 39,4 | 35,8 |
| 40,2 | 35,6 |
| 40,3 | 36,1 |
| 41,6 | 36,3 |
| 42,7 | 37,2 |
| 42,8 | 37,7 |
| 44,5 | 38,4 |
 |
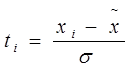Перейдем к нормированным значениям аргумента (табл.1.3):
Таблица 1.3.
|
| t(x) | F(tx) | t(y) | F(ty) |
| 1 | 2 | 3 | 4 | 5 |
| t1 | -1,6 | 0,0548 | -1,6 | 0,0548 |
| t2 | -1,3 | 0,0968 | -1,5 | 0,0668 |
| t3 | -1,2 | 0,1151 | -1,2 | 0,1151 |
| t4 | -1,2 | 0,1151 | -1,1 | 0,1357 |
| t5 | -1,1 | 0,1357 | -1,1 | 0,1357 |
| t6 | -1,1 | 0,1357 | -1,1 | 0,1357 |
| t7 | -0,9 | 0,1841 | -0,9 | 0,1841 |
| t8 | -0,9 | 0,1841 | -0,9 | 0,1841 |
| t9 | -0,6 | 0,2743 | -0,6 | 0,2743 |
| t10 | -0,4 | 0,3446 | -0,6 | 0,2743 |
| t11 | -0,4 | 0,3446 | -0,5 | 0,3085 |
| t12 | -0,3 | 0,3821 | -0,4 | 0,3446 |
| t13 | -0,3 | 0,3821 | -0,3 | 0,3821 |
| t14 | -0,2 | 0,4207 | -0,1 | 0,4602 |
| t15 | -0,2 | 0,4207 | -0,1 | 0,4602 |
| t16 | -0,2 | 0,4207 | -0,1 | 0,4602 |
| t17 | -0,1 | 0,4602 | -0,1 | 0,4602 |
| t18 | 0,1 | 0,5398 | -0,1 | 0,4602 |
| t19 | 0,3 | 0,6179 | 0,2 | 0,5793 |
| t20 | 0,4 | 0,6554 | 0,4 | 0,6554 |
| t21 | 0,6 | 0,7257 | 0,6 | 0,7257 |
| t22 | 0,6 | 0,7257 | 0,6 | 0,7257 |
| t23 | 0,6 | 0,7257 | 0,7 | 0,7580 |
| t24 | 0,7 | 0,7580 | 0,9 | 0,8159 |
| t25 | 1,0 | 0,8413 | 0,9 | 0,8159 |
| t26 | 1,0 | 0,8413 | 1,1 | 0,8643 |
| t27 | 1,4 | 0,9192 | 1,2 | 0,8846 |
| t28 | 1,7 | 0,9554 | 1,6 | 0,9452 |
| t29 | 1,7 | 0,9554 | 1,8 | 0,9641 |
| t30 | 2,2 | 0,9861 | 2,2 | 0,9861 |
Принимаем значения эмпирической функции распределения в точке t равным следующему значению (табл.1.4):
 |
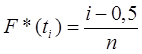где i= 1, 2,...,n. При t< t1 F*(t)=0, а при t>tn F*(t)=l.
Таблица 1.4.
|
| F*(ti) |
| 1 | 2 |
| 1 | 0,016667 |
| 2 | 0,05 |
| 3 | 0,083333 |
| 4 | 0,116667 |
| 5 | 0,15 |
| 6 | 0,183333 |
| 7 | 0,216667 |
| 8 | 0,25 |
| 9 | 0,283333 |
| 10 | 0,316667 |
| 11 | 0,35 |
| 12 | 0,383333 |
| 13 | 0,416667 |
| 14 | 0,45 |
| 15 | 0,483333 |
| 16 | 0,516667 |
| 17 | 0,55 |
| 18 | 0,583333 |
| 19 | 0,616667 |
| 20 | 0,65 |
| 21 | 0,683333 |
| 22 | 0,716667 |
| 23 | 0,75 |
| 24 | 0,783333 |
| 25 | 0,816667 |
| 26 | 0,85 |
| 27 | 0,883333 |
| 28 | 0,916667 |
| 29 | 0,95 |
| 30 | 0,983333 |
Определим максимальное значение модуля разности между эмпирической функцией распределения F*(t) и теоретической функцией для нормального закона распределения F(t) (значения F(t) представлены в табл.3.2):
 | |||
 | |||
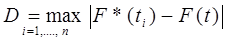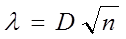и определяем величину:
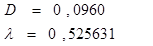Для признака x:
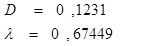Для признака y:
Затем по таблице определяем в зависимости от l вероятность Р(l), того что за счёт чисто случайных причин расхождение между F*(t) и F(t) будет не больше, чем фактически наблюдаемое.
При сравнительно больших Р(l) теоретический закон распределения можно считать совместимым с опытными данными.
Дата: 2019-04-23, просмотров: 215.
