Модель распределения
Курсовая работа по статистике
Работу выполнил ст. гр. ЭР-6-4 Шалыгин Д.А.
Московский государственный технологический университет «Станкин»
Кафедра «Производственный менеджмент»
Москва 2001
Раздел 1. Исследование модели распределения
Формирование выборочной совокупности
Обычно бывает затруднительно исследовать генеральную совокупность. Тогда проводят исследование выборочной совокупности, и его результаты распространяют на генеральную совокупность.
Наиболее часто для формирования выборочной совокупности применяют бесповторную случайную выборку. Случайный отбор организуют с помощью жребия, таблицы случайных чисел или программы, генерирующей квазислучайную последовательность чисел. Для этого единицы генеральной совокупности нумеруют. Данные, соответствующие выпавшим, номерам попадают в выборку. При этом повторяющиеся номера пропускаем.
Покажем применение таблицы случайных чисел. В табл. 1 приложения приведено пятьсот четырехзначных случайных чисел.
Рассмотрим пример получения выборки. Генеральная совокупность содержит значения восьми количественных экономических показателей для 100 предприятий. Она представлена в табл.2 приложения.
Наиболее проработанной в статистике является парная корреляция. Положим, нужно установить корреляционную связь между двумя показателями. В нашем случае мы изучаем связь между годовой балансовой прибылью (показатель 5) и электровооруженностью на одного работающего (показатель №7), выбираем в табл.1 приложения четырёхзначное число из 7-го столбца, 5-ой строки; т.к. сумма номеров показателей чётна, то из него берём правую половину; далее выбираем 30 неповторяющихся чисел. Затем из табл.2 приложения выбираем в соответствующих номерах строк 30 пар значений изучаемых показателей, в соответствии с этими данными получаем табл.1.1
Таблица 1.1
| № строки | 5 | 7 |
| 5 | 40,2 | 35,6 |
| 12 | 35,4 | 32,9 |
| 13 | 31,4 | 30,5 |
| 18 | 42,8 | 37,7 |
| 22 | 36,6 | 33,7 |
| 26 | 37,8 | 34,3 |
| 27 | 44,5 | 38,4 |
| 30 | 42,7 | 37,2 |
| 31 | 32,8 | 31,3 |
| 32 | 32,5 | 30,7 |
| 36 | 32,7 | 31,4 |
| 38 | 38,9 | 35,3 |
| 40 | 33,2 | 31,6 |
| 41 | 36,2 | 33,7 |
| 43 | 33,3 | 31,4 |
| 45 | 36,2 | 33,5 |
| 46 | 38,4 | 34,6 |
| 49 | 38,8 | 35,1 |
| 52 | 35,7 | 33,2 |
| 54 | 33,7 | 32 |
| 57 | 36,3 | 33,6 |
| 60 | 40,3 | 36,1 |
| 65 | 35,8 | 32,8 |
| 68 | 33,7 | 31,9 |
| 69 | 41,6 | 36,3 |
| 71 | 38,8 | 35 |
| 76 | 34,9 | 32,6 |
| 80 | 39,4 | 35,8 |
| 86 | 37,1 | 33,5 |
| 91 | 35,9 | 32,6 |
| 99 | 4 | 42,2 |
Раздел 2. Исследование взаимосвязи двух количественных признаков
Раздел 3. Изучение динамических рядов
Изучение сезонных явлений
Исследуем сезонные процессы в наших двух динамических рядах. При изучении сезонных явлений из уровней динамического ряда целесообразно вычесть значения, получаемые по уравнению тренда, которые отражают основную тенденцию развития.
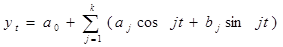При изучении периодических процессов в качестве аналитической модели используем ряд Фурье:
где k=1; j=1.
Для нахождения коэффициентов a0, aj, bj применяем метод наименьших квадратов.
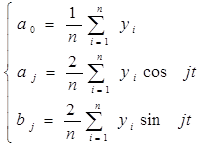Получаем:
Для признака x: Для признака y:
 |  |
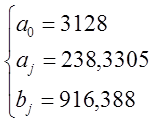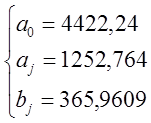Обычно для расчётов используют ежемесячные данные за один год или несколько лет. В этом случае интервал между двумя соседними месяцами принимают равным:
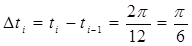
Построив модель сезонных колебаний, положим для уточнённого изучения основной тенденции a0 =0. Исключим сезонные колебания из уровней динамического ряда (табл.3.1.1).
Таблица 3.1.1
| xt | yt | |
| 2661,669 | 3613,236 | |
| 2875,587 | 3822,011 | |
| 2963,355 | 3982,202 | |
| 3123,42 | 4283,029 | |
| 3220,836 | 4428,087 | |
| 3326,98 | 4610,676 | |
| 3286,852 | 4566,172 | |
| 3263,324 | 4538,486 | |
| 3116,237 | 4319,251 | |
| 3036,962 | 4198,99 | |
| 2900,234 | 3993,958 | |
| 2894,491 | 3990,848 | |
| 2874,626 | 3974,423 | |
| 2997,766 | 4181,021 | |
| 3084,173 | 4339,299 | |
| 3262,659 | 4638,991 | |
| 3338,698 | 4783,995 | |
| 3444,038 | 4907,625 | |
| 3403,894 | 4924,979 | |
| 3381,141 | 4899,469 | |
| 3315,414 | 4682,148 | |
| 3157,719 | 4563,026 | |
| 3022,368 | 4358,052 | |
| 3017,432 | 4353,904 | |
| 2997,586 | 4365,623 |
Модель распределения
Курсовая работа по статистике
Работу выполнил ст. гр. ЭР-6-4 Шалыгин Д.А.
Московский государственный технологический университет «Станкин»
Кафедра «Производственный менеджмент»
Москва 2001
Раздел 1. Исследование модели распределения
Дата: 2019-04-23, просмотров: 175.
