Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Из логических соображений выдвинем предположение, что признак (названный нами y) зависит от второго исследуемого признака x.

Используя проведенное в первом разделе разбиение значений x на интервалы, построим аналитическую таблицу:

 

Аналитическая таблица исследования зависимости признака y от признака x

Группы предприятий по признаку x	Число предприятий в j-ой группе mj	Признак y
		Суммарное значение в группе	Среднее значение признака yi в j-ой группе на одно предприятие
31,4 – 34,02	8	250,8	31,3500
34,02 – 36,64	9	298,6	33,1778
36,64 – 39,26	6	207,8	34,6333
39,26 – 41,88	4	143,8	35,9500
41,88 – 44,5	3	113,3	37,7667

 

Далее рассчитываем общую дисперсию:

 

 

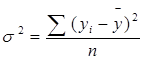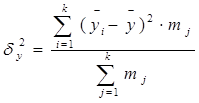где 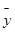 - среднее значение признака для всей выборки, и межгрупповую дисперсию:

 

 

где 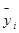 - среднее значение признака в j-й группе; m_j- численность j-й группы; k - число групп.

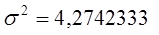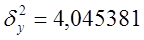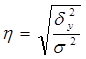Для оценки тесноты связи между признаками y и x рассчитываем корреляционное отношение:

 

 

Оценку тесноты связи признаков y и x проводим по шкале Чеддока:

-если 0,3<h£0,5, то теснота связи заметная;

-если 0,5<h£0,7, то теснота связи умеренная;

-если 0,7<h£0,9, то теснота связи высокая;

-если 0,9<h£0,9(9), то теснота связи весьма высокая.

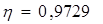2. Определение формы связи двух признаков

Примерное представление о виде зависимости y от x даёт линия, проведённая через точки, соответствующие групповым средним и полученные на основе аналитической таблицы следующим образом: среднему значению признака 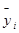 в j-ой группе ставится в соответствие не середина интервала группирования по признаку x, а среднее значение 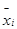, полученное из соответствующих интервалу значений признака x. Можно воспользоваться следующим приемом: построим все точки, соответствующие парам (х_i;у_i), в декартовой системе координат и провести линию через середины скоплений точек (График № 1).

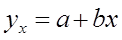Затем по справочнику плоских кривых и виду линии подбираем соответствующее уравнение регрессии. Однако не следует брать слишком сложное уравнение. В нашем случае берём линейную функцию:

 

Вычислив частные производные и приравняв их к нулю, получим систему линейных алгебраических уравнений относительно коэффициентов а и b. В нашем случае система уравнений имеет вид:

 

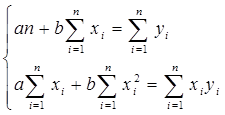
Решая эту систему уравнений относительно b, получим:

 

 

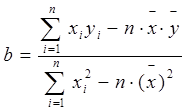
Решая первое уравнение относительно а, получим:

                                    

 

                                                                           

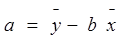
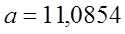
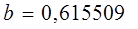
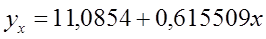                        Т.о.:          

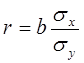Линейный коэффициент корреляции равен:

где s_x и s_y - средние квадратические отклонения признаков x и y.

                                                                                   

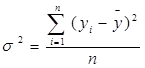Рассчитаем общую дисперсию:

 

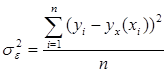и остаточную дисперсию:

 

где y_x(х_i) - значение величины y, рассчитанное по уравнению регрессии при подстановке в него значения x_i; y_i- значение величины y в исходной таблице, соответствующее значению x_i.

 

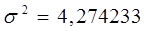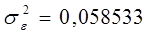Определим индекс корреляции:

 

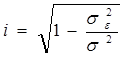Индекс корреляции принимает значения 0£ i £1.

                                                                                     

 

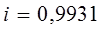
Т.к. i близок к единице, то связь между признаками хорошо описана выбранным уравнением регрессии. Для линейной зависимости дополнительным условием для такого заключения является близость значений r и i.                                                           

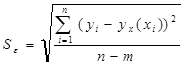Можно выбрать несколько видов уравнения регрессии. Наилучшим из них будет то уравнение, которому соответствует меньшая средняя квадратическая ошибка уравнения регрессии:

где m - число коэффициентов в уравнении регрессии.

                                                                                     

 

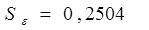
Принимая во внимание то, что мы имеем дело с малой выборкой, необходимо оценить значимость коэффициентов уравнения регрессии, а также индекса корреляции i и линейного коэффициента корреляции r. Значимость линейного коэффициента корреляции r оцениваем с помощью критерия Стьюдента. Фактическое значение критерия Стьюдента равно:

   

 

 

                            

                                                                      

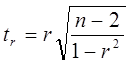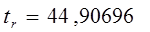
Критическое (предельное) значение критерия Стьюдента t_k, берем из табл.4 приложения, задаваясь уровнем значимости a=5,0 и имея число степеней свободы равное:

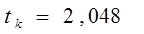k=n-2

Если t_r>t_k, то величину линейного коэффициента корреляции считаем значимой и можем использовать в расчетах.

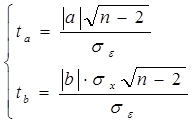Значимость коэффициентов уравнения регрессии а и b также оцениваем с помощью критерия Стьюдента. Расчетные значения критерия Стьюдента равны:

 

 

Учитывая, что число степеней свободы также равно k=n-2, сравнение фактических значений критерия Стьюдента ведем с уже найденным критическим значением t_k.

Если t_a>t_k, t_b>t_k, то соответствующий коэффициент уравнения регрессии значим, и мы можем им пользоваться. Значимость индекса корреляции определяем с помощью критерия Фишера. Фактическое значение критерия Фишера равно:

 

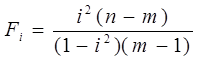где m - число коэффициентов в уравнении регрессии.

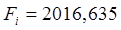
Табличное значение критерия Фишера F_k; определяется по табл.5 приложения, задаваясь уравнением значимости a и числом степеней свободы k₁=m-l; k₂=n-m.

 

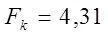Если Fi>Fk, то величину индекса корреляции считаем значимой и можем ее использовать в расчетах.

Если коэффициенты а и b, а также линейный коэффициент корреляции r и индекс корреляции i значимы, то все наши расчеты и выводы, опирающиеся на эти величины, правомерны и мы можем использовать полученное уравнение регрессии для прогноза. Ошибка прогноза будет зависеть, в частности, от остаточной дисперсии s²_e.