Приклад 1.

Знайдемо функцію Рімана для рівняння

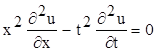.                          (7.1)

Зробивши заміну змінних

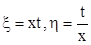
рівняння (7.1) приводиться до канонічного вигляду

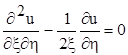
при цьому будемо мати a = 0, b = -.

Звернемося тепер до відшукання фунції Рімана v(x, h, x₁, h₁). Згідно загальної теорії, вона повинна задовольняти спряженому рівнянню

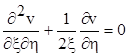                                (7.2)

та умовам на характеристиках, які проходять через точку (x₁, h₁):

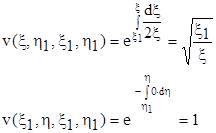                          (7.3)

неважко вконатися, що функція

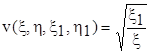
задовільнює як рівнянню (7.2), так і умовам (7.3), слід, це і є шукана функція Рімана.

Приклад 2.

Знайдемо функцію Рімана для рівняння

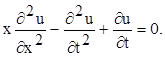(x > 0)                               (7.4)

приведемо рівняння (7.4) до канонічного вигляду, для чого складемо рівняння характерстик

xdt² – dx² = 0

це рівняння має два різних інтеграла

+ = C₁, - = C₁,

слід, треба ввести нові змінні x та h за формулами

x = + , h = -  (x >0)

приєднаємо до цих рівностей ще одну залежність

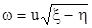
тоді рівняння (7.4) перетвориться до канонічного вигляду:

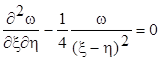
при цьому будемо мати a = 0, b = 0.

Для відшукання функії Рімана нам потрібно знайти частинний розв’язок спряженого рівняння

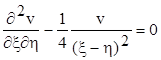                             (7.5)

який задовольняв би слідуючим умовам на характеристиках, проведених через точку (x₁, h₁)

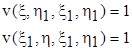                                 (7.6)

Будемо шукати розв’язок рівняння (7.1) у вигляді v = G(s), де

s =.

Тоді для G(s) ми отримаємо слідуюче рівняння:

s(1-s)G’’(s) + (1-2s)G’(s) - G(s) = 0

Це рівняння частинним випадком гіпер геометрічного рівняння Гаусса

s(1-s)y’’ + [g - (1 + a + b)s]y’ - aby = 0

при a = b = , g = 1.

Рівняння Гаусса припускає частинний розв’язок у вигляді гіпергеометрічного ряду

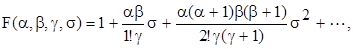
який збігається абсолютно при |s| < 1.

Звідки ясно, що взявши

v = G(s) = F 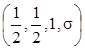= 1 +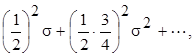

ми задовільним рівнянню (7.5) та усмовам (7.6). Слід, функція

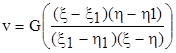
і є функцією Рімана.

Приклад 3.

Знайдемо функцію Рімана для телеграфного рівняння

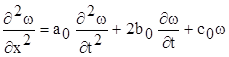
якщо ввести нову функцію u(x, t) поклавши

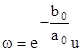                                           (7.7)

то рівняння (7.7) більш просту форму

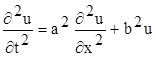,                                 (7.8)

де a = , b = .

За допомогою заміни змінних

x = (x + at), h = (x - at)

приведемо рівняння (7.8) до канонічного вигляду

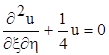
при цьому маємо a = b = 0.

Функція Рімана повинна задовільнювати спряженому рівнянню

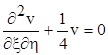,                                      (7.9)

та на характеристиках x = x₁, h = h₁ дорівнює одиниці.

Будемо шукати розв’язок рівняння (7.9) у вигляді

.

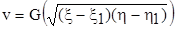Підставивши цей вираз та пізначивши через l корінь 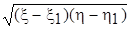, знайдемо, що функція v задовільнює звичайному диференційному рівнянню

G’’(l) + G’(l)+G(l)=0,

Лінійно незалежними розв’язками якого є функція Бесселя нульового порядку

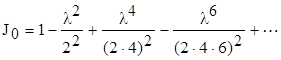
та функція Неймана N₀(l), основною властивістю якої є 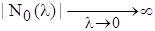, слід, вона не може бути шуканою функцією.

Тобто, якщо взяти

v = J₀(l)

отримаємо розв’язок рівняння (7.9), який обертається на характерис-тиках x = x₁, h = h₁ у одиницю, оскільки тут l = 0.

Таким чином, функція Рімана знайдена, вона має вигляд:

.

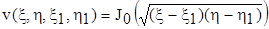Висновок.

В даній роботі розглянуто задачу Гурса для телеграфного рівняння. Було доведено, що розв’язок цієї задачі існує та що він єдиний. Завдяки використанню метода Рімана ми отримали цей розв’язок у явному вигляді. На прикладах ми показали, що знаходження функції Рімана зводиться до розв’язання звичайних диференйійних рівнянь, таких як рівняння Бесселя або гіпергеометричного рівняння Гаусса.