Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Шаг 1. Определить все результирующие понятия, или выходы системы. Это может быть набор диагнозов, рекомендаций, советов системы.

Шаг 2. Определить все входные понятия, или факторы, от которых зависит результат работы системы.

Шаг 3. Установить промежуточные понятия, участвующие в рассуждениях экспертов, если они есть.

Шаг 4. Для всех понятий найти обобщающие и уточняющие понятия, т.е. установить иерархии объектов.

Шаг 5. Для объектов, участвующих в рассуждениях, определить свойства и их значения.

Шаг 6. Попытаться определить другие связи, и все в целом отразить графически.

Шаг 7. Убрать лишние связи, объекты, обсудить структуру с экспертом, дополнить, если надо, с возвратом к шагам 1-6.

Функциональная структура отражает модель рассуждений и принятия решения, которой пользуется эксперт при решении задачи.

Обычно функциональная структура представляется в виде каузальных отношений и может быть позднее формализована в виде коротких правил “если - то”, или в виде семантических сетей.

Представить функциональную структуру можно в виде таблицы, графа (дерева решений) или предложений на естественном языке. Наглядные формы предпочтительны.

Часто в моделях рассуждений присутствуют нечеткие понятия – “ часто”,”много”,”очень”,”высокий”,”большой” и др. Для их представления в базе знаний используется так называемая нечеткая логика, автор которой – Л.Заде, предложил простой формализм для таких понятий. Этот формализм использует понятие нечеткой функции принадлежности, которая отражает численно на шкале [0,10] или [0,1] степень уверенности эксперта в том, что конкретное значение можно отнести к данному нечеткому понятию.

 

 

МОДЕЛИ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

1. Продукционная модель.

Продукционная модель, или модель, основанная на правилах, позволяет представлять знания в виде предложений типа:

Если (условие), то (действие).

Записываются эти правила обычно в виде:

ЕСЛИ А₁,А₂,…,А_n ТО В.

Под условием понимается некоторое предложение – образ, по которому осуществляется поиск в базе знаний, а под действием – действия, выполняемые при успешном исходе поиска (они м.б. промежуточными, выступающими далее как условие, и терминальными или целевыми, завершающими работу системы).

«Условие» называют иногда «Посылкой», а «Действие» - «Выводом» или «Заключением».

Условия А₁,А₂,…,А_n обычно называют фактами. С помощью фактов описывается текущее состояние предметной области. Факты могут быть истинными, ложными, либо, в общем случае, правдоподобными, когда истинность факта допускается с некоторой степенью уверенности.

Действие В трактуется как добавление нового факта в описание текущего состояния предметной области.

В упрощенном виде описание предметной области с помощью правил (продукций) базируется на следующих основных предположениях об устройстве предметной области. ПО может быть описана в виде множества фактов и множества правил.

Факты – это истинные высказывания (повествовательные предложения) об объектах или явлениях предметной области.

Правила описывают причинно-следственные связи между фактами (в общем случае и между правилами тоже) - как истинность одних фактов влияет на истинность других.

Продукционные модели могут отражать следующие виды отношений:

- ситуация ® действие,

- посылка ® заключение,

- причина ® следствие.

В продукционных системах используются два основных способа реализации механизма вывода:

1. Прямой вывод, или вывод от данных;

2. Обратный вывод, или вывод от цели.

В первом случае идут от известных данных (фактов) и на каждом шаге вывода к этим фактам применяют все возможные правила, которые порождают новые факты, и так до тех пор, пока не будет порожден факт-цель.

Для применения правила используется процесс сопоставления известных фактов с правилами и, если факты согласуются с посылками в правиле, то правило применяется.

Во втором случае вывод идет в обратном направлении – от поставленной цели. Если цель согласуется с заключением правила, то посылку правила принимают за подцель или гипотезу, и этот процесс повторяется до тех пор, пока не будет получено совпадение подцели с известными фактиами.

 

Пример: Набор правил:

П1: Если “отдых – летом” и ”человек – активный”, то “ехать в горы”.

П2: Если “любит солнце”, то “отдых - летом”.

Предположим, в систему поступили данные: “человек – активный” и “любит солнце”.

Прямой вывод:

1-й проход.

Шаг 1. Пробуем П1, не работает (не хватает данных “отдых – летом”).

Шаг 2. Пробуем П2, работает, в базу поступил факт “отдых летом”.

2-й проход.

Шаг 3. Пробуем П1, работает, активизирует цель “ехать в горы”, которая и выступает как совет, который дает ЭС.

Обратный вывод: - подтвердить выбранную цель при помощи имеющихся правил и данных.

1-й проход.

Шаг 1. Цель – “ехать в горы”. Пробуем П1 – данных “отдых – летом” нет, они становятся новой целью, и ищется правило, где она в правой части.

Шаг 2. Цель “отдых – летом”. Правило П2 подтверждает цель и активизирует ее.

2-й проход.

Шаг 3. Пробуем П1, искомая цель подтверждается.

Продукционная модель чаще всего применяется в промышленных ЭС.

достоинства: наглядность, высокая модульность, легкость внесения дополнений и изменений и простота логического вывода.

Разработано большое количество ЭС, используемых в самых различных областях, в том числе и в нашей прикладной области.

При использовании продукционной модели база знаний состоит из набора правил. Программа, управляющая перебором правил, называется машиной вывода. Вывод может быть прямым (от данных к поиску цели) или обратным (от цели для ее подтверждения – к данным). Данные – это исходные факты, на основании которых запускается машина вывода – программа, перебирающая правила в базе знаний.

2. Семантическая сеть.

Семантическая означает смысловая. Семантика – наука об отношения между символами и объектами, которые они обозначают, т.е. наука, определяющая смысл знаков.

Семантическая сеть - это ориентированный граф, вершины которого – понятия, а дуги – отношения между ними.

“Понятия” это обычно абстрактные или конкретные объекты, а “отношения” – это связи типа: ‘это”, “быть частью”, “принадлежать”, “любит”.

Отношения бывают 3-х типов:

- Класс, к которому принадлежит данное понятие,

- Свойство, выделяющее понятие из всех прочих понятий этого класса,

- примеры данного понятия или элемента класса.

 

Наиболее часто используют следующие отношения:

- связи типа “часть – целое”,

- функциональные связи (соответствуют глаголам: “производит”, “влияет” и т.д.),

- количественные (>,<,= т.д.)

- пространственные (далеко от, близко от, за, под, над, …),

- временные (раньше, позже, в течение, …),

- атрибутивные (иметь свойство, иметь значение, …),

- логические (и, или, не) др.

Проблема поиска решения в базе знаний типа семантическая сеть сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, соответствующей поставленному вопросу.

Пример.

Двигатель

Цвет

Красный

      Значение              

                    Свойство                                                                 Имеет частью            

Вид транспорта

Автомобиль

Волга

                                             Это                                      Это               

  

   Принадлежит                 Любит

                                         

Иванов

 

 

2. Фреймовая модель.

Фрейм предложен М. Минским в 70-е годы как структура знаний для восприятия пространственных сцен. Это модель, как и семантическая сеть, имеет глубокое психологическое обоснование.

Под фреймом понимается абстрактный образ или ситуация. Напримекр слово “комната” вызывает у слушающих образ комнаты: “жилое помещение с четырьмя стенами, полом, потолком, окнами и дверью, площадью 6 – 20 кв. метров.

       Из этого описания ничего нельзя убрать, но в нем есть “дырки”  или “слоты”, - это н00езаполненные значения некоторых атрибутов - количество окон, высота потолка, покрытие пола и другие.

       В теории фреймов такой образ называется фреймом. Фреймом называется также и формализованная модель для отображения образа.

       Структура фрейма:

       (Имя фрейма:

            имя 1-го слота (значение 1-го слота ),

            имя 2-го слота (значение 2-го слота ),

              . . .

            имя N-го слота (значение N-го слота)).

Или в виде таблицы.

 

Имя фрейма
Имя слота	Тип слота	Значение слота	Присоединение

В таблице дополнительные столбцы предназнвчены для описания типа слоота и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов.

Например, слот “дата рождения” может содержать процедуру для вычисления возраста. Тогда естественно слот “возраст” оказывается ненужным. Данная процедура подключается автоматически и называется демоном.  Если процедура активизируется по запросу, она называется слугой.

С использованием присоединенных процедур можно запрограммировать любую процедуру вывода на фреймовой сети. Механизм управления выводом организуется следующим образом. Сначала запускается одна из присоединенных процедур некоторого фрейма, называемого образцом. Образец – это, по сути, фрейм-прототип, т.е. у него заполнены не все слоты, а только те, которые описывают связи данного фрейма с другими. Затем в силу необходимости, посредством пересылки сообщений, последовательно запускаются присоединенные процедуры других фреймов и таким образом осуществляется вывод.

В качестве значения слота может выступать имя другого фрейма; так образуют сети фреймов.

Слоты могут содержать фасеты, которые задают дипазон или перечень его возможных значений (например, слот “возраст” может содержать фасет “максимальный возраст”

Различают фреймы – образцы или прототипы, хранящиеся в базе знаний, и фреймы – экземпляры, которые создаются для отображения реальных ситуаций на основе поступающих данных.

Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через:

- фреймы – структуры,

- фреймы – сценарии,

- фреймы – ситуации.

Основным преимуществом фреймов как модели представления знаний является способность отражать концептуальную основу организации памяти человека, а также ее гибкость, наглядность и универсальность. Но она обладает высокой степенью формализации и сложностью (низкое быстродействие машины вывода).

 

4. Формальные логические модели.

Традиционно в представлении знаний выделяют формальные логические модели, основанные на классическом исчислении предикатов 1 порядка, когда предметная область или задача описывается в виде набора аксиом (правильных высказываний или объектов) и задаются правила построения новых объектов из других правильных объектов системы (правила вывода).

Пример.

1)высказывание: a>b представляется термом p(a,b) (двуместный предикат), где p – предикатный символ, заменяющий знак “>";

2)высказывание “аппаратная ах – исправна” представляется Q(x);

3)теорема Пифагора может быть представлена термом:

                     P_![P₂ (P₃(x),P₃ (y)),P₃(z)]

В качестве предикатных символов могут использоваться следющие:

Ø - НЕВЕРНО ЧТО (ЗНАК ОТРИЦАНИЯ);

Ç - И (ЗНАК КОНЪЮНКЦИИ);

È - ИЛИ (ЗНАК ДИЗЪЮНКЦИИ);

® - ЕСЛИ … ТО (ЗНАК ИМЛИКАЦИИ);

Û - ТОГДА, КОГДА (ЗНАК ЭКВИВАЛЕНТНОСТИ);

" - ДЛЯ ВСЯКОГО ( ЗНАК КВАНТОРА ОБЩНОСТИ);

$ - СУЩЕСТВУЕТ (ЗНАК КВАНТОРА СУЩЕСТВОВАНИЯ).

В различных логических системах используются разнообразные правила вывода. Приведем два наиболее распространенные.

Правило подстановки. В формуле, которая уже выведена, можно вместо некоторого высказывания подставить любое другое присоблюдении условия: подстановка должна быть сделана во всех местах вхождения заменяемого высказывания в данную формулу.

Правило заключения. Если a и a®b являются истинными высказываниями посылками, тогда и высказывание заключение b также истина. Записывается правило в виде дроби

 

 

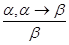
Особенность систем представления знаний заключается в том, сто они моделируют деятельность человека, осуществляемую часто в неформальном виде. Модели представления знаний имеют дело с информацией, получаемой от экспертов, которая часто носит качественный и противоречивый характер. Для обработки с помощью ЭВМ такая информация должна быть приведена к однозначному формализованному виду. Методологией формализованного представления знаний является логика.

 

2. СТРУКТУРА И РЕЖИМЫ РАБОТЫ ЭС

Знания, которыми обладает специалист в какой-либо облас­ти (дисциплине), можно разделить на формализованные (точные) и неформализованные (неточные). Формализованные знания фор­мулируются в книгах и руководствах в виде общих и строгих суждений (законов, формул, моделей, алгоритмов и т.п.), от­ражающих универсальные знания. Неформализованные знания, как правило, не попадают в книги и руководства в связи с их конкретностью, субъективностью, и приблизительностью. Знания этого рода являются результатом обобщения многолетнего опыты работы и интуиции специалистов. Они обычно представляют со­бой многообразие эмпирических (эвристических) приемов и пра­вил.

В зависимости от того, какие знания преобладают в той или иной области (дисциплине), ее относят к формализованным (если преобладают неточные знания) описательным областям. Задачи, решаемые на основе точных знаний, называют формали­зованными, а задачи, решаемые с помощью неточных знаний,- неформализованными. (Речь идет не о неформализуемых, а о не­формализованных задачах, т.е. о задачах, которые, возможно, и формализуемы, но эта формализация пока неизвестна.

Традиционное программирование в качестве основы для раз­работки программы использует алгоритм, т.е. формализованное знание. Поэтому до недавнего времени считалось, что ЭВМ не приспособлены для решения неформализованные задач. Расшире­ние сферы использования ЭВМ показало, что неформализованные задачи составляют очень важный класс задач, вероятно, значи­тельно больший, чем класс формализованных задач. Неумение решать неформализованные задачи сдерживает внедрение ЭВМ в описательные науки. Основной задачей информатики является внедрение ее методов в описательные науки и дисциплины. На основании этого можно утверждать, что исследования в области ЭС занимают значительное место в информатике.

Ньюэлл предложил относить к неформализованным задачам те, которые обладают одной или несколькими из следующих осо­бенностей:

алгоритмическое решение задачи неизвестно (хотя, возмож­но, и существует) или не может быть использовано из-за огра­ниченности ресурсов ЭВМ (времени, памяти);

задача не может быть определена в числовой форме (требу­ется символьное представление);

цели задачи не могут быть выражены в терминах точно оп­ределенной целевой функции.

Как правило, неформализованные задачи обладают неполно­той, ошибочностью, неоднозначностью и (или) противоречи­востью знаний (как данных, так и используемых правил преоб­разования).

Экспертные системы не отвергают и не заменяют традицион­ного подхода к программированию, они отличаются от традици­онных программ тем, что ориентированы на решение неформали­зованных задач и обладают следующими особенностями:

алгоритм решений не известен заранее, а строится самой ЭС с помощью символических рассуждений, базирующихся на эв­ристических приемах;

ясность полученных решений, т.е. система "осознает" в терминах пользователя, как она получила решение;

способность анализа и объяснения своих действий и знаний;

способность приобретения новых знаний от пользовате­ля-эксперта, не знающего программирования, и изменения в со­ответствии с ними своего поведения;

обеспечение "дружественного", как правило, естествен­но-языкового (ЕЯ) интерфейса с пользователем.

Обычно к ЭС относят системы, основанные на знаниях, т.е. системы, вычислительная возможность которых является в пер­вую очередь следствием их наращиваемой базы знаний (БЗ) и только во вторую очередь определяется используемыми метода­ми. Методы инженерии знаний (методы ЭС) в значительной сте­пени инвариантны тому, в каких областях они могут применять­ся. Области применения ЭС весьма разнообразны: военные при­ложения, медицина, электроника, вычислительная техника, гео­логия, математика, космос, сельское хозяйство, управление, финансы, юриспруденция и т.д. Более критичны методы инжене­рии знаний к типу решаемых задач. В настоящее время ЭС ис­пользуются при решении задач следующих типов: принятие реше­ний в условиях неопределенности (неполноты), интерпретация символов и сигналов, предсказание, диагностика, конструиро­вание, планирование, управление, контроль и др.