Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

     1. ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ.

В основе геометрических методов лежит понятие меры близости объектов в  n-мерном признаковом пространстве описаний. Центральной задачей при создании систем распознавания является выбор типа меры близости.

Меру близости необходимо выбирать таким образом, чтобы она, с одной стороны, отвечала представлению разработчика о близости объектов рассматриваемых классов, а с другой - позволяла бы упростить процедуры синтеза оптимальных частных алгоритмов.

Сущность меры близости применительно к рассматриваемому классу задач покажем на примере двух классов в 2-х мерном пространстве описаний.

 

 

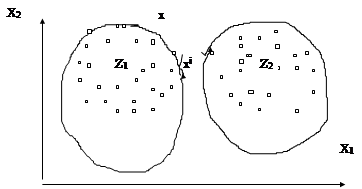Интерпретация рисунка приводит к естественному выводу о предпочтительности отнесения объекта Х к первому классу. В то же время классификация объекта Хⁱ  вызывает затруднения и необходимы расчеты.

Очевидно, что классификация образов с помощью функции расстояния эффективен только в тех случаях, когда классы образов обнаруживают тенденцию к кластеризации (группированию).

Поскольку близость классифицируемого образа к образам класса будет использоваться в качестве критерия для его классификации, назовем такой подход классификацией образов по критерию минимума расстояния.

Классы могут быть представлены путем перечисления членов класса (как на рисунку: точки в кластерах) или с помощью эталонных образов (например, центральными объектами z₁ и z₂).

Заметим также, что в рассматриваемом классе задач описания объектов являются векторными.

Рассмотрим М классов. Пусть эти классы допускают их представление с помощью эталонных образов Z₁,Z₂, . . .,Z_m.  Евклидово расстояние между произвольным вектором образа Х  и i-м эталоном определяется следующим выражением:

                                   _____________                                

       D_i = || X - Z_i || = √( X - Z_i )^/  ( X - Z_i )                                                  (1)

 где || Х || - Евклидова норма;

 

          х₁

          х₂

Х =   х₃       - вектор образа распознаваемого объекта;

                   :

                  х_n

 

          z₁

Z =    :   - вектор образа эталона класса;

          z_n

 

      

         _{n           1}

|| Х || = [Σ X_j²  ]²

        ^j=1

 X ^/ = ( x₁ ,x₂ , . . .,x_n) - транспонированный вектор;

 

X ^/ Z - скалярное произведение;

       _n

X^/ Z = Σ X_j^/ Z_j

      ^{j = 1}  

Классификатор, построенный по принципу минимума расстояния, вычисляет расстояние, отделяющее классифицируемый образ Х от эталона каждого класса, и зачисляет этот образ в класс,, оказавшийся ближайшим к нему. Другими словами, образ Х приписывается к классу W_{i ,}  если условие D_{i <} D_j для всех j ¹ i .

Путем несложных преобразований исходно формуле (1) можно придать более удобный для вычислений вид.

 

d_i (X) = X^/ Z_i - 1/2  Z_i^/ Z_i,              i = 1,2,...,M,

 

где образ Х относится к классу W_i, если условие d_i (X) > d_j (X) справедливо для всех   j ¹ i.

 

Пример:

      z_{1 . . .}  z₅

z₁^/  = ( 1 2 6 3 1 )           z₂^/ = ( 6 4 3 2 1 )

        x^/  = ( 1 3 5 2 1 )

 

                                   

d₁(x) = ( 1 3 5 2 1 )     -1/2 ( 1 2 6 3 1 )    =       ( 1+6+30+6+1 ) - 1/2 ( 1+4+36+9+1 ) =

 

 

= 44 - 1/2 51 = 18.5;

d₂(x) = (6+12+15+4+1) - 1/2 (36+16+9+4+1) = 38 - 1/2 66 =5

d₁(x) > d₂(x) , поэтому образ х  принадлежит первому классу.  

 Меры сходства не исчерпываются расстояниями. В качестве примера можно привести не метрическую функцию сходства

           z x ^/

s ( x , z ) = -----------,

       || x || || z ||      

представляющую собой косинус угла, образованного векторами  X и Z. Этой мерой целесообразно пользоваться, когда кластеры располагаются вдоль главных осей или растянуты вдоль лучей, направленных от начала координат.  

 

 

 

         

 

 

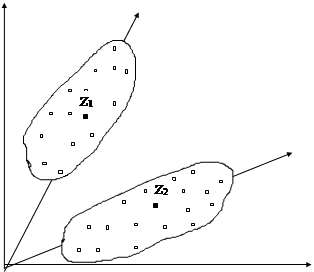Однако использование данной меры связано с определенными ограничениями: достаточное отстояние кластеров друг от друга и от начала координат.

Для двоичных признаков (признаки принимают значения либо `` 0`` либо ``1``) может использоваться мера Танимото

               z x ^/

s ( x , z ) = ------------------- .

    x ^/ x + z ^/ z - x ^/ z

Перечисленные меры близости не учитывают корреляционные связи между признаками. Устранить этот недостаток позволяет критерий известный по названием расстояние Махаланобиса, определяемое для образов  x и m как

d = ( x - m ) ^/  с ^-1 ( x - m ),

где  c - ковариационная матрица совокупности образов, m - вектор средних значений, а х - представляет образ с переменными характеристиками(классифицируемый образ).

 

2. ЛОГИЧЕСКИЕ МЕТОДЫ

Объекты классов и реализация представляются в виде булевых функций:

Ω_i  = f_i (x₁, . . . , x_n) , i = 1, . . . ,k

и  G = (x₁ , . . . , x_n).

Заданы правила использования булевых функций при распознавании:

W = (w₁ , . . . , w_n).

Процедура распознавания состоит в определении неизвестной функции

 F(Ω_{1 , . . . ,}Ω_k),удовлетворяющей уравнению

 

_

G (x₁,. . . , x_n ) + F(Ω₁ , . . . , Ω_k)= I,                      (1)

Где  F - совокупность булевых функций априорного описания.                          

 

Пример:

                                   F(Ω₁) = x₁x₂+x₃  или 110 + 001

 Ω_i = f_1i + f_2i  

                                  F(Ω₂) = x₁x₃+x₂  или 101 + 010

 

 

Правило классификации:

                       _                     _

 G ЄΩ_i,  если G + f₁ = I или  G + f₂ = I .

                                           _                        

Пусть G = x₁ x₂ или 110 ( G = 001).

Найти  F такую, чтобы выполнялось равенство 1.

 

           _

          G + f₁ = 001 + 110 = 111 = I

 Ω₁ :    _

          G + f₂ = 001 + 001 = 001 ¹ I

           _

           G + f₁ = 001 + 101 = 101 ¹ I

Ω:₂:    _

          G + f₂ = 001 + 010 = 011 ¹ I

Вывод: G принадлежит Ω₁.

 

3. СТРУКТУРНЫЕ МЕТОДЫ

При структурном подходе к распознаванию признаками служат образы, называемые непроизводными элементами, а также отношения между ними, характеризующие структуру образа.

Для описания образов через непроизводные элементы и их отношения специальный язык образов.

Правила такого языка, позволяющие составлять образы из непроизводных элементов, называется  порождающей грамматикой.

Пример:

Заданы непроизводные элементы:

                             в        d

         а       с     

и правило объединения: головная часть присоединяется к хвостовой по прямым углом и записывается, например, ав, т.е.

                      в

             а

Фигура             будет иметь следующую грамматическую структуру: авсd.

В основе процедур(алгоритмов) распознавания лежат правила грамматического разбора.

4. ВЕРОЯТНОСТНЫЕ МЕТОДЫ

Статистический подход основывается на математических правилах классификации, которые формулируются и выводятся в терминах математической статистики.

Пример. Пусть совокупность объектов подразделена на два класса -Ω_{1  и} Ω_2, а для характеристики объектов используется один признак х. Известны описания классов - условные плотности распределения вероятностей значений признака объектов 1-го и 2-го классов, т.е. функции f₁(x) и f₂(x), а также априорные вероятности появления объектов 1-го и 2-го классов: р(Ω₁) и р(Ω₂).

В результате эксперимента определено значение признака распознаваемого объекта, равное х⁰.

Определить, к какому классу относится объект ?

Обозначим через х₀ некоторое пока не определенное значение признака х и условимся о следующем правиле принятия решений:

n если измеренное значение признака распознаваемого объекта х⁰>х_0, то объект будем относить ко второму классу;

n если х⁰< х₀ - к первому.

f(x)       x Q2               x0             Q1   R1   R2

 

Если объект относится к первому классу, а его считают объектом второго класса, то совершена ошибка, которая называется ошибкой 1-го рода.

Условная вероятность ошибки 1-го рода равна

     ∞

Q₁ = ʃ f₁(х) d(x)

     x₀

Если объект относится ко второму классу, а его считают объектом 1-го класса, то совершена ошибка, которую называют ошибкой второго рада.

Условная вероятность ошибки 2-го рада равна

    x₀   

Q₂  = ʃ f₂(x)

  -∞

Для определения значения х₀ введем понятие платежной матрицы

= || с || ₌   с₁₁ с₁₂      ,

                         с₂₁ с₂₂

где с₁₁  и с₂₂ - потери, связанные с правильными решениями, а с₁₂ и с₂₁  - потери, связанные с совершением ошибок первого и второго рода соответственно.

Значение х₀ определяется в зависимости от значения коэффициента правдоподобия

l (x) = f₂(x)/f₁(x).

Значению х₀ соответствует критическое (пороговое) значение  l (x) = l₀

          р(Ω₁)(c₁₂-c₁₁)

l₀ = 

           p(Ω₂)(c₂₁-c₂₂)

Значение х₀ позволяет оптимальным образом (в смысле минимума среднего риска) разделить признаковое пространство на две области:  R₁ и R₂.

Область R₁  состоит из значений х ≤ х₀, для которых  l(x) ≤ l₀ а R₂ - из значений х > х₀,  для которых  l(x) > l₀

Поэтому решение об отнесении объекта к первому классу следует принимать, если значение коэффициента правдоподобия меньше его критического значения, и ко второму классу, если больше.

На практике при построении систем распознавания возможны ситуации, когда известны:

а) f₁(x), f₂(x), р(Ω₁), р(Ω₂) и ||с|

б) f₁(x), f₂(x)  и платежная матрица, но не известны р(Ω₁), р(Ω₂).

в) f₁(x), f₂(x), но не известны ни р(Ω₁), р(Ω₂) ни платежная матрица.

В каждой из этих ситуаций применяются свои критерии распознавания, а именно - критерий Байеса, минимаксный критерий, критерий Неймана-Пирсона.

Признаковая информация представляется в виде таблиц распознавания вида

Классы	Градации признака хi
	хi1	xi2	...	xim
А1	0.6	0.5	...	0.1
А2	0.7	0.4	...	0.2
...	...	...	...
An	0.1	0.2	...	0.1

 

Наиболее часто используется критерий Байеса, который выражается формулой

                     p ( A_j ) p ( b_k / A_j )

p ( A_j / b_k ) =                          

                      M

                      S p(A_i) p(b_k/A_i)

                                   i=1

где

p(A_j/b_k) - вероятность гипотезы о принадлежности реализации b_к  к j-му классу.

              B_k = { x₁^l, . . . , x_n^k, . . . , x_N^p},

              х_i   - признаки классов, l,k,p -  градации признаков,  

p(A_j) - априорная вероятность проявления j-го класса(A_j);

 

p(b_k/A_j)  - условная вероятность проявления признаков реализации b_k у класса   A_j.

M - количество классов.

 

P(A_j) = m_j / F ( m_j - количество объектов j-го класса, F - суммарное количество объектов всех классов). 

                       N

P(b_k/A_j) = П p(x_i^l/A_j), где p(x_i^l/A_j) - вероятность проявления l-ой градации i-го

                  i=1

признака у класса A_j.

 

N - количество признаков в рабочем словаре.

 

В результате вычислений по формуле Байеса получим значения p(A_j/b_k)  для каждого класса.

Решение о принадлежности реализации к конкретному классу принимается по максимуму вычисленной вероятности.

 

ЭКСПЕРТНЫЕ СИСТЕМЫ

КОНЦЕПЦИЯ ЗНАНИЙ

При изучении интеллектуальных систем традиционно возникает вопрос, – что же такое знания и чем они отличаются от обычных данных, десятилетиями обрабатываемых ЭВМ.

Можно предложить несколько рабочих определений, в рамках которых это становится очевидным.

Данные – это отдельные факты, характеризующие объекты, процессы и явления в предметной области, а также их свойства. Данные интерпретируются специальными программами. Они пассивны. Нет содержательной информации.

При обработке на ЭАМ данные трансформируются, условно проходя следующие этапы:

- данные как результат измерений и наблюдений;

- данные на материальных носителях информации (таблицы, протоколы, справочники);

- модели (структуры) данных в виде диаграмм, графиков, функций;

- данные в компьютере на языке описания данных;

- базы данных на машинных носителях.

Знания связаны с данными, основываются на них, но представляют собой результат мыслительной деятельности человека, обобщают его опыт, приобретенный в ходе выполнения какой-либо практической деятельности. Они получаются эмпирическим путем.

Знания – это выявленные закономерности предметной области (принципы, связи, законы), позволяющие решать задачи в этой области. Они могут быть активны, т.е. определенные действия при выполнении соответствующих условий.

В отличие от данных знания обладают следующими свойствами:

· внутренней интерпретируемостью – вместе с информацией в БЗ представлены информационные структуры, позволяющие не только хранить знания, но и использовать их;

· структурированностью – выполняется декомпозиция сложных объектов на более простые и установление связей между ними;

· связанностью – отражаются закономерности относительно фактов, процессов, явлений и причинно-следственные отношения между ними;

· активностью –знания предполагают целенаправленное использование информации, способность управлять информационными процессами по решению определенных задач.

Все эти свойства знаний в конечном итоге должны обеспечить возможность СИИ моделировать рассуждения человека при решении прикладных задач – со знаниями тесно связано понятие процедуры получения решений задач (стратегии обработки знаний). В системах обработки знаний такую процедуру называют механизмом вывода, логическим выводом или машиной вывода. Принципы построения механизма вывода в СИИ определяются способом представления знаний и видом моделируемых рассуждений.

При обработке на ЭВМ знания трансформируются аналогично данным:

- знания в памяти человека как результат мышления;

- материальные носители знаний (учебники, методические пособия);_

- поле знаний - условное описание основных объектов предметной области, их атрибутов и закономерностей, их связывающих;

- знания, описанные на языках представления знаний (продукционные языки, семантические сети, фреймы и т.д.);

- базы знаний.

   Часто используются такие определения знаний:

Знания – это хорошо структурированные данные, и данные о данных, или метаданные.

Существует множество способов определять понятия. Один из широко применяемых способов основан на идее интенсионала.

Интенсионал понятия – это определение через понятие более высокого уровня абстракции с указанием специфических свойств. Этот способ определяет знания.

Другой способ определяет понятие через перечисление понятий более низкого уровня иерархии или фактов, относящихся к определяемому. Это есть определение через данные, или экстенсионал, понятия.

Пример: интенсионал: курсант- это учащийся военного училища.

Экстенсионал: курсант- это Иванов, Петров….

Для хранения данных используются базы данных (для них характерны большой объем и относительно небольшая удельная стоимость информации), для хранения знаний – базы знаний – основа любой интеллектуальной системы.

Знания могут быть классифицированы по следующим категориям:

- поверхностные – знания о видимых взаимосвязях между отдельными событиями и фактами в предметной области;

- глубинные – абстракции, аналогии, схемы, отображающие структуру и процессы в предметной области.

Знания, на которые опирается человек, решая те или иную задачу, существенно разнородны.

Это прежде всего:

· понятийные знания (набор понятий и их взаимосвязи);

· конструктивные знания (знания о структуре и взамодествии частей различных объектов);

· процедурные знания (методы, алгоритмы и программы решения различных задач);

· фактографические знания (количественные и качественные характеристики объектов, явлений и их элементов).

 

Современные ЭС работают в основном с поверхностными знаниями, т. к. в настоящее время нет адекватных моделей, позволяющих работать с глубинными знаниями.

Кроме того, знания можно разделить на процедурные и декларативные. Исторически первичными были процедурные знания, т.е. знания, ”растворенные” в алгоритмах. Они управляли данными. Для их изменения требовалось изменять программы. Однако с развитием ИИ приоритет данных постепенно изменялся, и все большая часть знаний сосредотачивалась в структурах данных (таблицы, списки, абстрактные типы данных), т.е. увеличивалась роль декларативных знаний.

Сегодня знания приобрели чисто декларативную форму, т.е. знаниями считаются предложения, записанные на языках представления знаний, приближенных к естественному и понятных неспециалистам.

Существуют десятки моделей (или языков) представления знаний для различных предметных областей. Большинство из них м.б. сведено к следующим классам:

- продукционные;

- семантические сети;

- фреймы;

- формальные логические модели.

ПОЛЕ ЗНАНИЙ

Одна из наиболее творческих процедур при построении ЭС – процедура концептуального анализа полученных знаний или структурирование.

Структурирование – это процесс создания полуформализованного описания предметной области. Такое полуформализованное описание называется полем знаний. Обычно оно создается в графической форме.

Поле знаний Р_z можно описать следующим образом:

                P_z=<S_k,S_f>,

где S_k  - концептуальная структура предметной области;

S_f – функциональная структура предметной области.

Концептуальная структура, или модель предметной области, служит для описания ее объектов и отношений между ними, т.е. можно сказать, что концептуальная модель S_k представляет собой следующее:

                      S_k=<A,R>,

где А – множество объектов предметной области;

  R – множество отношений, связывающих объекты.

Множество отношений представляет собой связи между объектами. При помощи этих отношений инженер по знаниям фиксирует концептуальное устройство предметной области, иерархию понятий, свойство и структуру объектов. Разработка концептуальной структуры имеет самостоятельное значение, не зависимое от конечной цели – разработки экспертных систем. Эта структура может служить для целей обучения, повышения квалификации, для прогнозирования, объяснения, реструктурирования и т.п.