Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием. Другими словами - это составной оператор, который устанавливает условие для чего-то, что будет истинным. Если условие выполнено, утверждение верно.
Символ: А®В.
Пример:
Высказывание1: А –«Четырехугольник - квадрат» Высказывание2: В –«Четырехугольник - ромб»
Импликация: А®В = «ЕСЛИ четырехугольник – квадрат, ТО четырехугольник - ромб.»
Из определения логического условия, вытекает такие понятия как необходимые и достаточные условия.
Необходимое условие – это то условие, которое обязательно должно быть правдой для того, что бы все выражение следования оказалось правдой. Без выполнения этого условия истинность высказывания невозможна. Т.е. если А®В истинно, то В – необходимое условие. Быть ромбом – необходимое условие, что бы быть квадратом, без этого не получится квадрат.
Однако далеко не каждый ромб обязан быть квадратом, поэтому обратная испликация может оказаться неверной. В®А = «ЕСЛИ четырехугольник – ромб, ТО четырехугольник - квадрат.» - ложно! А является достаточным условием для В. Быть квадратом – достаточное основание для того, что бы быть ромбом.
Очень важно понимать, что использование условного оператора всегда позволяет получить истинное значение, за одним исключением. Если условие верно, а следствие оказывается ложью – результат операции следования тоже будет ложь.
Почему это важно?
Пример: предположим, мы разрабатываем систему безопасности, которая должна срабатывать в случае, если кто-то вносит в экзаменационную аудиторию включенный мобильник. В этом случае наша система безопасности озвучивает случайным образом пункт из реально существующих (истинных ) предупреждений (например, «выключите мобильник» или «за списывание вы будете удалены с экзамена» или «использование включенных мобильников на экзамене запрещено» и т.д.). Разработчик системы должен заботиться не только об истинности произошедшего события (пронесен или не пронесен мобильник), но и об истинности озвученного правила (существует такое или нет). Но что происходит во всех других случаях, разработчик не продумывает, потому что его задача выглядит как условие
«ЕСЛИ на экзамен пронесли мобильник, ТО озвучить существующее правило».
Рассмотрим различные возможные ситуации:
Ситуация 1 (условие ложное, следствие истинно): Студент, не идущий на экзамен, прошел мимо системы безопасности, и система озвучила «использование включенных мобильников на экзамене запрещено». Система озвучила настоящее правило, но это не имеет значения, поскольку студент и не собирался на экзамен. Т.е. на самом деле система может озвучивать все что угодно, в случае, если условие не выполнено, при этом корректность ее работы не противоречит условию, заданному в ТЗ.
Ситуация 2 (условие ложное, следствие ложное): Студент вошел на экзамен с бананом в руке, а система безопасности выдала «с бананами на экзамене присутствовать запрещено». Система выдала ложный пункт правил, но это не имеет значения, поскольку студент не принес мобильника. Звучит забавно, но не противоречит ТЗ. Система работает именно так, как и ожидал разработчик.
Ситуация 3 (Условие верно, следствие верно): Студент входит в аудиторию с включенным мобильником и слышит предупреждение «выключите мобильник». Наше условие выполнено, система сработала как надо. Значит система работает?
Ситуация 4 (условие верно, следствие неверно): Студент входит в аудиторию с включенным мобильником и слышит предупреждение «с бананами на экзамене присутствовать запрещено». Очевидно, что именно эта ситуация иллюстрирует, что система не работает. Условие ЕСЛИ.., ТО… привело к ошибочному результату.
Пример компьютерной программы (написанная в псевдокоде), которая иллюстрирует, что происходит. В качестве входных данных функции предположим, что мы можем передать только 1 или 0. 1 представляет истину для простого оператора, а 0 представляет ложь.
Function WhatsTheTruthValue (a,b){ if (a > 0){ var t = 3*b; if (t === 0){ print "function crashed"; return; } } print "function works"; }В этой программе мы передаем значения (1 или 0) в функцию, и функция пытается умножить 3 на значение b. Если эта операция выдает значение 0, функция выводит на экран «сбой функции» и больше не продолжается. В противном случае он выводит «функция работает» на экран. Теперь давайте посмотрим на все возможные операции этой функции.
| Вводимые переменные | Результат |
| а=1; b=1 | «функция работает» |
| а=1; b=0 | «сбой функции» |
| а=0; b=1 | «функция работает» |
| а=0; b=0 | «функция работает» |
В итоге выводимый результат зависит и от самой функции и от переданной в нее переменной.
Операторы можно комбинировать для создания довольно сложных составных операторов. Когда вы комбинируете операторы, может оказаться трудно определить, к какому типу операторов относится весь оператор в целом. Например, что это за утверждение такое: p --> q & r v s & t
В этом выражении - четыре оператора, но невозможно определить, кто является основным оператором. Важно знать, кто является основным оператором, потому что именно так мы определяем истинное значение утверждения в целом. Перепишем это же выражение так: p --> (q & ((r v s) & t)). Иногда неудобно использовать скобки рядом друг с другом, поэтому используют скобки и пишут так: p --> (q & [(r v s) & t]).
Теперь вы можете сказать, что это за утверждение? Если вы считаете «условие», вы правы. Как и в математике, мы находим значение истинности для утверждений во внутренних скобках, а затем можем найти для утверждения в целом. Последний оператор, для которого вы находите значение истинности, является оператором самой большой области действия и определяет, с каким составным оператором вы работаете. Чтобы увидеть это, давайте присвоим следующие значения истинности нашим переменным: p = true; q = false; r = false; s = true and t = true.
Если мы хотим определить значение истинности утверждения в целом, мы начнем с самой внутренней дизъюнкции, поскольку это самое внутреннее составное утверждение.
· r = false, s = true, значит (r v s)=true;
· (r v s)=true, t = true значит ((r v s) & t)=true;
· q = false, ((r v s) & t)=true, значит (q & [(r v s) & t])= false;
· p = true, (q & [(r v s) & t])= false, значит все выражение будет иметь ложное значение.
Очень важно знать последовательность выполнение операторов, а так же порядок наследования.
Таблицы истинности
Это таблицы, которые позволяют определить значение истинности, в случае применения одного и того же оператора к выражениям, обладающим разными значениями истинности.
Оператор отрицания:
| А | 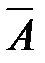
|
| 0 | 1 |
| 1 | 0 |
Конъюнкция (И):
| А | В | А&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (ИЛИ):
| А | В | АÚB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Импликация (условие)
| А | В | АÚB |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблицы истинности можно использовать для сложного логического выражения:
p --> (q & [(r v s) & t])
| p | q | r | s | t | p | à | (q | & | [(r | Ú | s) | & | t]) | |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | |||||||||||
| 1 | 0 | 1 | ||||||||||||
| 1 | 0 | |||||||||||||
| 0 |
Виды умозаключений (доказательств)
Логика - это изучение стандартов правильного мышления. Все умозаключения в логике делятся на две широкие категории: дедуктивные и индуктивные. Каждый тип умозаключений, если он четко сформулирован, может быть классифицирован как дедуктивный или индуктивный.
Дедуктивное умозаключение выдвигается таким образом, что бы быть истинным, если все его предпосылки верны.
Индуктивное умозаключение, наоборот, выдвигается с совершенно другой целью. Связь предпосылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из предпосылок и может содержать информацию, отсутствующую в них. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.
Следующие умозаключения являются дедуктивными, поскольку каждое из них призвано убедительно показать, что заключение должно быть верным, если все предпосылки верны:
Умозаключение 1:
Все киты являются млекопитающими.
Все млекопитающие являются животными.
Поэтому, безусловно, все киты должны быть животными.
Умозаключение 2:
На ужин будут макароны или на ужин будет рис.Эт
Это не тот случай, когда на ужин будет рис.
Поэтому наверняка у нас будут макароны на ужин.
Умозаключение 3:
Если крыша протекает, значит потолок протекает.
Если потолок протекает, то ковер намокнет.
Так что, конечно, если крыша протекает, то ковер намокнет.
Напротив, следующие умозаключения являются индуктивными, потому что каждый из них стремится показать только то, что заключение, вероятно, хотя и не обязательно, верно:
Умозаключение 4:
За всю историю человечества в Сочи, в июле никогда не было снега.
Поэтому весьма вероятно, хотя и не совсем точно, что в Сочи в июле следующего года не будет снега.
Умозаключение 5:
The Rolling Stones распродали билеты на каждый концерт, который они дали за последние пятьдесят лет.
Поэтому вполне вероятно, что билеты на их следующий концерт будут распроданы.
Умозаключение 6:
Снег шел в течение последних пяти дней.
Все прогнозы погоды предсказывают, что завтра будет больше осадков.
Поэтому, хотя это и не совсем точно, разумно сделать вывод, что завтра будет снег.
Если вы составляете умозаключение и хотите убедиться, что ваше умозаключение является дедуктивным, поместите в заключение слова, которые указывают на наличие дедуктивного мышления. Такие слова, как: «должно», «обязательно», «наверняка», «определенно», и «абсолютно», указывают на то, что заключение составлено таким образом, чтобы быть верным, если все предпосылки верны. Обратите внимание, что каждый только что приведенный дедуктивный аргумент содержит слово дедуктивного индикатора в своем заключении.
Если вы хотите выяснить, является ли умозаключение индуктивным, используйте в заключении слова, которые указывают на наличие индуктивного мышления. Такие слова, как «вероятно», «возможно» и «разумно сделать вывод», предполагают, что вы намерены аргументировать, чтобы показать, что заключение, вероятно, но не обязательно, верно, если все предпосылки верны. Каждый из приведенных выше индуктивных аргументов содержит в своем выводе слово индуктивного индикатора.
Итак, для дедуктивных методов проведения умозаключений характерно то, что если умозаключение имеет истинное значение, предпосылки должны быть истинными. Но истинных предпосылок недостаточно для истинности умозаключения.
Пример:
Предпосылка 1: вода закипает при 100°С - истина
Предпосылка 2: вода состоит из атомов водорода и кислорода – истина
Умозаключение: значит вода кипит, потому что состоит из молекул кислорода и водорода – ложь
Несмотря на то, что обе предпосылки являются истинными, заключение оказалось ложью. Это произошло из-за того, что предпосылки находятся в неверных взаимоотношениях друг с другом.
Поэтому необходимо, что бы предпосылки оказывались в правильных взаимоотношениях друг другом, и составляли правильную структуру – правильную форму умозаключения.
Пример:
Предпосылка 1: ЕСЛИ вода находится при 100°С, ТО она закипает - истина
Предпосылка 2: вода находится при 100°С – истина
Умозаключение: значит вода закипает
Пример:
Предпосылка 1: Все студенты учатся - истина
Предпосылка 2: Все учащиеся умеют читать – истина
Умозаключение: Значит все студенты умеют читать
Дедуктивные умозаключения, которые приводят к ложному выводу, при условии, что предпосылки истинны имеют неправильную форму.
Самый простой способ проверить правильность составления умозаключения – это задать себе вопрос «Если я предполагаю, что предпосылки верны, возможно ли, что заключение может быть ложный?" Если вы можете ответить «да», то умозаключение неправильное, а правильное, если вы отвечаете «нет». Один из способов определить, может ли заключение быть ложным, - найти контрпример (реальная ситуация, когда предпосылки верны, но заключение все еще ложно). Мы можем назвать это «интуитивным тестом» на достоверность.
Такой интуитивный тест работает даже, если вы плохо знаете или вообще не знаете о чем идет речь.
Пример:
Предпосылка 1: Все сепульки расфуоливаются
Предпосылка 2: Бука - сепулька
Умозаключение: Значит Бука расфусоливается
Звучит странно, но, даже не зная, кто такие сепульки и Бука и что значит расфусоливаться, можно сказать, что умозаключение истинно. Этот пример показывает, что на самом деле не истинность предпосылок делает истинным умозаключение, а именно форма по каторому составлено умозаключение делает его истинным.
Теперь посмотрим на примеры, где истинные предпосылки не приводят к истинности умозаключения, так как структура (форма) является неправильной.
Пример:
Предпосылка 1: Все школьники учатся - истина
Предпосылка 2: Некоторые учащиеся умеют читать
Умозаключение: Все школьники умеют читать
Это неправильное умозаключение. Оно очень похоже на пример со студентами за одним исключением. В предпосылке 2 появилось слово «некоторые» и именно это слово сделало умозаключение неправильным. Некоторые означает – по крайней мере один. А значит может быть хотя бы еще один учащийся, который не умеет читать.
Пример:
Предпосылка 1: Если вы программист, то знакомы с JavaScript
Предпосылка 2: Вы знакомы с JavaScript
Умозаключение: Значит вы – программист
Обратите внимание, что первая предпосылка говорит нам, что из того, что вы программист следует, что вы знакомы с JavaScript. Это ничего не говорит нам о том, программист ли вы, если знакомы с JavaScript.
Дата: 2019-04-23, просмотров: 390.