Оператор отрицания
Оператор отрицание – единственный оператор, который обрабатывает одно простое высказывание (монадический оператор). Если простое утверждение истинно, размещение перед ним (или над ним) символа отрицания делает составное утверждение ложным. Если простое утверждение ложно, но перед ним ставится отрицание, что делает сложное утверждение истинным.
Символ: ~ «высказывание» (тильда) или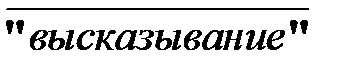 
(верхнее подчеркивание)
Пример:
Высказывание А –«Петр на лекции»
Отрицание - ~А – «Это не тот случай, когда Петр на лекции»
Очень важно, что бы простое высказывание не изменилось, а оператор оказался бы применен. Если сказать «Петр не на лекции» простое высказывание меняется. Поэтому с точки зрения применения оператора правильно использовать формулировку «Это не тот случай, когда Петр на лекции».
Конъюкция (логическое умножение)
Конъюкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Символ: «высказывание» & «высказывание» (амперсанд) или «высказывание» AND «высказывание» или «высказывание» И «высказывание»
Пример:
Высказывание1: А –«Петр на лекции» Высказывание2: В –«Маша в кафе»
Конъюкция: А&В=А×В= Петр на лекции и Маша в кафе.
Если любое из высказываний ложно, то и всё сложное высказывание целиком ложно. Т.е. если Петр на лекции, а Маша рядом с ним (т.е. не в кафе), то утверждать «Петр на лекции и Маша в кафе» было бы ложью.
Дизъюнкция (логическое сложение)
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Символ: «высказывание» Ú «высказывание» или «высказывание» OR «высказывание» или «высказывание» ИЛИ «высказывание»
Пример:
Высказывание1: А –«Петр на лекции» Высказывание2: В –«Маша в кафе»
Дизъюкция: АÚВ=А+В= Петр на лекции или Маша в кафе.
Очевидно, что если одно из высказываний истинно, то все сложное выражение тоже истинно, вне зависимости от того является ли истинным второе высказывание.
НЕ ПУТАТЬ с «исключающим ИЛИ» XOR, которое принимает истинное значание только если одно высказывание имеет истинность противоположную второму (т.е. если первое истинно, то второе ложное и наоборот).
Таблицы истинности
Это таблицы, которые позволяют определить значение истинности, в случае применения одного и того же оператора к выражениям, обладающим разными значениями истинности.
Оператор отрицания:
| А |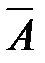 
|
| 0 | 1 |
| 1 | 0 |
Конъюнкция (И):
| А | В | А&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (ИЛИ):
| А | В | АÚB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Импликация (условие)
| А | В | АÚB |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблицы истинности можно использовать для сложного логического выражения:
p --> (q & [(r v s) & t])
| p | q | r | s | t | p | à | (q | & | [(r | Ú | s) | & | t]) | |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | |||||||||||
| 1 | 0 | 1 | ||||||||||||
| 1 | 0 | |||||||||||||
| 0 |
Виды умозаключений (доказательств)
Логика - это изучение стандартов правильного мышления. Все умозаключения в логике делятся на две широкие категории: дедуктивные и индуктивные. Каждый тип умозаключений, если он четко сформулирован, может быть классифицирован как дедуктивный или индуктивный.
Дедуктивное умозаключение выдвигается таким образом, что бы быть истинным, если все его предпосылки верны.
Индуктивное умозаключение, наоборот, выдвигается с совершенно другой целью. Связь предпосылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из предпосылок и может содержать информацию, отсутствующую в них. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.
Следующие умозаключения являются дедуктивными, поскольку каждое из них призвано убедительно показать, что заключение должно быть верным, если все предпосылки верны:
Умозаключение 1:
Все киты являются млекопитающими.
Все млекопитающие являются животными.
Поэтому, безусловно, все киты должны быть животными.
Умозаключение 2:
На ужин будут макароны или на ужин будет рис.Эт
Это не тот случай, когда на ужин будет рис.
Поэтому наверняка у нас будут макароны на ужин.
Умозаключение 3:
Если крыша протекает, значит потолок протекает.
Если потолок протекает, то ковер намокнет.
Так что, конечно, если крыша протекает, то ковер намокнет.
Напротив, следующие умозаключения являются индуктивными, потому что каждый из них стремится показать только то, что заключение, вероятно, хотя и не обязательно, верно:
Умозаключение 4:
За всю историю человечества в Сочи, в июле никогда не было снега.
Поэтому весьма вероятно, хотя и не совсем точно, что в Сочи в июле следующего года не будет снега.
Умозаключение 5:
The Rolling Stones распродали билеты на каждый концерт, который они дали за последние пятьдесят лет.
Поэтому вполне вероятно, что билеты на их следующий концерт будут распроданы.
Умозаключение 6:
Снег шел в течение последних пяти дней.
Все прогнозы погоды предсказывают, что завтра будет больше осадков.
Поэтому, хотя это и не совсем точно, разумно сделать вывод, что завтра будет снег.
Если вы составляете умозаключение и хотите убедиться, что ваше умозаключение является дедуктивным, поместите в заключение слова, которые указывают на наличие дедуктивного мышления. Такие слова, как: «должно», «обязательно», «наверняка», «определенно», и «абсолютно», указывают на то, что заключение составлено таким образом, чтобы быть верным, если все предпосылки верны. Обратите внимание, что каждый только что приведенный дедуктивный аргумент содержит слово дедуктивного индикатора в своем заключении.
Если вы хотите выяснить, является ли умозаключение индуктивным, используйте в заключении слова, которые указывают на наличие индуктивного мышления. Такие слова, как «вероятно», «возможно» и «разумно сделать вывод», предполагают, что вы намерены аргументировать, чтобы показать, что заключение, вероятно, но не обязательно, верно, если все предпосылки верны. Каждый из приведенных выше индуктивных аргументов содержит в своем выводе слово индуктивного индикатора.
Итак, для дедуктивных методов проведения умозаключений характерно то, что если умозаключение имеет истинное значение, предпосылки должны быть истинными. Но истинных предпосылок недостаточно для истинности умозаключения.
Пример:
Предпосылка 1: вода закипает при 100°С - истина
Предпосылка 2: вода состоит из атомов водорода и кислорода – истина
Умозаключение: значит вода кипит, потому что состоит из молекул кислорода и водорода – ложь
Несмотря на то, что обе предпосылки являются истинными, заключение оказалось ложью. Это произошло из-за того, что предпосылки находятся в неверных взаимоотношениях друг с другом.
Поэтому необходимо, что бы предпосылки оказывались в правильных взаимоотношениях друг другом, и составляли правильную структуру – правильную форму умозаключения.
Пример:
Предпосылка 1: ЕСЛИ вода находится при 100°С, ТО она закипает - истина
Предпосылка 2: вода находится при 100°С – истина
Умозаключение: значит вода закипает
Пример:
Предпосылка 1: Все студенты учатся - истина
Предпосылка 2: Все учащиеся умеют читать – истина
Умозаключение: Значит все студенты умеют читать
Дедуктивные умозаключения, которые приводят к ложному выводу, при условии, что предпосылки истинны имеют неправильную форму.
Самый простой способ проверить правильность составления умозаключения – это задать себе вопрос «Если я предполагаю, что предпосылки верны, возможно ли, что заключение может быть ложный?" Если вы можете ответить «да», то умозаключение неправильное, а правильное, если вы отвечаете «нет». Один из способов определить, может ли заключение быть ложным, - найти контрпример (реальная ситуация, когда предпосылки верны, но заключение все еще ложно). Мы можем назвать это «интуитивным тестом» на достоверность.
Такой интуитивный тест работает даже, если вы плохо знаете или вообще не знаете о чем идет речь.
Пример:
Предпосылка 1: Все сепульки расфуоливаются
Предпосылка 2: Бука - сепулька
Умозаключение: Значит Бука расфусоливается
Звучит странно, но, даже не зная, кто такие сепульки и Бука и что значит расфусоливаться, можно сказать, что умозаключение истинно. Этот пример показывает, что на самом деле не истинность предпосылок делает истинным умозаключение, а именно форма по каторому составлено умозаключение делает его истинным.
Теперь посмотрим на примеры, где истинные предпосылки не приводят к истинности умозаключения, так как структура (форма) является неправильной.
Пример:
Предпосылка 1: Все школьники учатся - истина
Предпосылка 2: Некоторые учащиеся умеют читать
Умозаключение: Все школьники умеют читать
Это неправильное умозаключение. Оно очень похоже на пример со студентами за одним исключением. В предпосылке 2 появилось слово «некоторые» и именно это слово сделало умозаключение неправильным. Некоторые означает – по крайней мере один. А значит может быть хотя бы еще один учащийся, который не умеет читать.
Пример:
Предпосылка 1: Если вы программист, то знакомы с JavaScript
Предпосылка 2: Вы знакомы с JavaScript
Умозаключение: Значит вы – программист
Обратите внимание, что первая предпосылка говорит нам, что из того, что вы программист следует, что вы знакомы с JavaScript. Это ничего не говорит нам о том, программист ли вы, если знакомы с JavaScript.
Modus Ponens
Правило отделения или гипотетический силлогизм. Состоит из двух предпосылок и следствия. В первой предпосылке говорится об отношениях двух терминов А и В, во второй об истинности А. На основании этого делается вывод об истинности В.
ЕСЛИ А, то В
А
Значит В
Пример:
Предпосылка 1: Если у человека Грипп (А) – человек болен (В)
Предпосылка 2: У человека грипп (А)
Умозаключение: Значит человек болен (В)
Modus Tollens
Состоит из двух предпосылок и следствия. В первой предпосылке говорится об отношениях двух терминов А и В, во второй о ложности В. На основании этого делается вывод о том, что В - ложь.
ЕСЛИ А, то В
НЕ В
Значит НЕ А
Пример:
Предпосылка 1: Если вы проходите курс по информатике (А), то вы очень занятой студент (В)
Предпосылка 2: Иван не очень занятой студнет (не В)
Умозаключение: Значит Иван не проходит курс по информатике(не А)
Подтверждение последствия
Эта ошибка связана с правилом Modus ponens
ЕСЛИ А, то В
А
Значит В
Ошибочное умозаключение выглядит так
ЕСЛИ А, то В
В
Значит А
Пример:
Предпосылка 1: Если у человека Грипп (А) – человек болен (В)
Предпосылка 2: Человек болен (В)
Умозаключение: Значит у него грипп (А)
Отрицание условия
Ошибка, связанная с неправильным применением правила Modus Tollens
ЕСЛИ А, то В
НЕ В
Значит НЕ А
Ошибочное умозаключение:
ЕСЛИ А, то В
НЕ А
Значит НЕ В
Пример:
Предпосылка 1: Если вы проходите курс по информатике (А), то вы очень занятой студент (В)
Предпосылка 2: Вы не проходите курс по информатике (не А)
Умозаключение: Значит вы не очень занятой студент (не В)
Логика и критическое мышление. Связь с информатикой.
На этой лекции мы рассмотрим фундаментальные основы формальной логики и увидим как логическое мышление и логические концепции применяются для проектирования и создания цифровых устройств. Приобретая навыки логического анализа, вы не только приобретете важные жизненные навыки, но и лучше поймете, как работают компьютеры, что в конечном итоге сделает вас лучшим техником.
Логика - это наука, которая устанавливает правила для упорядоченного мышления, в то время как критическое мышление – это мышление с применением этих правил.
Многие люди на протяжении веков глубоко задумывались о мышлении, и в результате был предложен, проверен и найден ряд стандартов или критериев, которые оказались надежными руководствами для обоснованного суждения о достижение истины. В качестве примера такого критерия рассмотрим статистическое мышление. Чтобы узнать о большой совокупности вещей, мы иногда исследуем выборку, а затем делаем выводы о совокупности в целом на основе того, что мы наблюдаем в выборке. Здравый смысл заключается в том, что чем больше выборка по отношению ко всей популяции, тем более вероятно, что заключение будет верным. Также здравый смысл заключается в том, что чем более случайно выбран образец, тем более вероятно, что вывод будет верным.
Таким образом, критическое мышление - это более, чем просто мышление какими-то субъективными критериями. Скорее, это мышление на основе критериев, которые были проверены и признаны надежными руководящими принципами для правильного суждения и достижения правды по рассматриваемому вопросу. Кто-то, кто принимает каждое важное решение на основе «бросания костей», занимается критериальным мышлением: бросание костей является критерием этого человека. (Бросание костей - это древняя форма гадания, при которой кости животных выбрасывают на коврик, а рисунок интерпретируется, как правило, шаманом, духовным читателем или гадалкой.) Однако такой человек не является критически мыслящим - по крайней мере в том смысле, с котором понятие «критическое мышление» используются сегодня - потому что его или ее критерий не был проверен и признан надежным руководством установлении истины и здравому суждению.
Что бы понять как связана логическое мышление и информатика, необходимо понять как работают («думают») машины. Рассмотрим самую простую модель, описывающую этот процесс – «машину Тьюринга».
Модель была изобретена учёным-компьютерщиком Аланом Тьюрингом, которого многие считают отцом цифровых вычислений. Тьюринг понял, что все вычислительные проблемы можно разбить на очень простой язык, цифровой язык: 0 и 1. Один из способов понять концепцию Тьюринга – использование терминов двух состояний: «включено» или «выключено», «истинно» или «ложно», «внутри» или «снаружи»;«да» и «нет». Во многих отношениях выключатель света на вашей стене - это цифровая машина. Когда выключатель света включен, он находится в одном состоянии, а когда он выключен, он находится в другом - и это единственные два состояния, в которых может находиться выключатель света. Хотя с этим выключателем можно передать немного информации, просто посмотрев на него, мы можем сказать, в каком состоянии находится свет (предположим, на секунду, что вы не можете видеть фактический свет, которым управляет переключатель).
Все современные компьютеры по своей сути очень сложные машины Тьюринга: очень быстро включают и выключают множество переключателей.
Бинарная модель, является основным языком, который понимают микропроцессоры на вашем компьютере. На гораздо более высоком уровне люди пишут код на языках программирования, которые компьютеры компилируют в то, что они могут обрабатывать. Именно этот программный код нам сейчас нужно рассмотреть, чтобы понять, как логика играет роль.
Компьютеры выполняют повторяемые задачи предсказуемым образом. Когда вы открываете текстовый редактор или играете в компьютерную игру, компьютер работает с набором команд или инструкций, которые написала команда программистов, и эти инструкции сообщают компьютеру, что делать и когда он должен их выполнять. Эти инструкции всегда делают одно и то же, и, когда программа написана хорошо, она выполняет их последовательно и без ошибок.
Эти инструкции называются «алгоритмами». Алгоритм - это не конкретный расчет, а метод, который используется при выполнении расчета. Некоторые называют алгоритм рецептом. Проще говоря, алгоритм - это повторяемый набор шагов, которые могут обрабатывать входные данные и которые обеспечивают предсказуемый, последовательный результат.
Когда программисты пишут компьютерные программы, они, по сути, пишут рецепты. Программы написаны в виде набора процедур, которые определяют, что компьютер должен делать в различных обстоятельствах. Например, вы можете написать компьютерную программу, которая складывает два числа вместе. Пользователь компьютера может указать числа, которые он хочет сложить, и ваш алгоритм выполнит операцию сложения и выдаст результат. Вы можете написать свою программу на определенном языке, таком как JavaScript или C++ и этот язык - который облегчает использование людьми - компилируется в биты и байты, чтобы компьютер мог понять его. Но это все еще алгоритм.
Сейчас мы приближаемся к пониманию взаимосвязи между информатикой и логикой. Логика следует этой алгоритмической модели, описывая непротиворечивое отношение идей друг к другу. Она предоставляет набор рецептов, которые мы можем использовать для организации мышления. Логика - это наука, которая анализирует концепции и идеи и пытается выработать правила упорядоченного мышления и найти ложные заключения, приводящие к неправильному мышлению. Компьютеры используют программы для обработки данных и выдают какие-то результаты, такие как изображения, музыка, электронные таблицы и онлайн-курсы. Так как эти две вещи связаны?
Вот простая компьютерная программа (написанная в псевдокоде - не настоящий язык программирования, а обучающая структура, которое мы можем использовать, чтобы записывать алгоритмы):
for (x=0; x < 7; x++){
If x is Even Then
print "Ешь макароны на ужин"
Else
print "Ешь салат на ужин"
}
Такая часть кода (подпрограмма) называется «циклом for» и будет увеличивать значение x на 1 каждый раз в цикле, изменяя х от 0 до 6. Это алгоритм.
В этой конкретной программе цикл for проверяет значение переменной x, которая изменяется (увеличивается на 1) каждый раз в цикле. Если текущее значение x в цикле является четным, то программа напечатает предложение «Ешь макароны на ужин». Если значение x отличается от чётного - условие «else», - программа выведет предложение «Ешь салат на ужин». Поскольку число, присвоенное x, является целым числом, оно может быть только нечетным или четным, поэтому мы знаем, что условие else для x всегда будет нечетным.
Рассмотрим как такая программа связана с логической аргументацией. Мы можем очень легко перевести эту компьютерную программу в доказательство с использованием формальной логики. Вместо цикла for мы будем использовать модель физического календаря, дни в котором изменяют значение. Другими словами, дни недели становятся числом х нашего выражения, и с каждым днем у нас появляется новое значение х. Теперь мы можем попробовать написать логическое выражение, которое позволит определить что семья будет есть в данный конкретный день.
Для примера мы начнем с дедуктивного силлогизма, называемого дизъюнктивным силлогизмом (логическое ИЛИ). Такой силлогизм принимает значение истина в случае, когда истинно не менее одного высказывания, составляющего этот силлогизм.
Предпосылка 1: День может быть четным ИЛИ нечетным;
Предпосылка 2: Сегодня день, который не является четным;
Вывод: Сегодня – нечетный день.
К сожалению, такое выражение не позволит нам определить, что же будет есть семья. Поэтому нужно добавить еще один силлогизм – Modus ponens (правило «вывода»). Для составления необходимого нам выражения, этот силлогизм выглядит так:
Предпосылка 1: ЕСЛИ день четный, ТО мы едим макароны
Предпосылка 2: день четный;
Вывод: поэтому мы едим макароны.
Конечно, нам нужен еще один силлогизм для нечетных дней:
Предпосылка 1: Если день нечетный, то мы едим салат;
Предпосылка 2: день нечетный;
Вывод: поэтому мы едим салат.
Теперь мы можем объединить их в одно выражение:
Дано: текущий день недели
Предпосылка 1: либо день нечетный, либо день четный
Предпосылка 2: если день четный, то мы едим макароны
Предпосылка 3: если день нечетный, то мы едим салат
Предпосылка 4: Это не тот случай, когда день [нечетный / четный]
Предпосылка 5: день [четный / нечетный]
Вывод: поэтому мы едим [макароны / салат]
Вы заметите, что запись компьютерной программы намного проще. Но мы иллюстрируем то, что компьютерная программа может быть переведена в стандартную логическую форму и наоборот. Мы увидим, почему это работает и вы увидите тесную связь между компьютерной логикой и формальной логикой. Если вы сможете научиться применять логические рамки к вашему мышлению в повседневной жизни, это поможет вам продумать, как писать лучшие компьютерные программы - и наоборот! Основатель Apple Стив Джобс сказал: «Я думаю, что все должны научиться программировать компьютер, потому что он учит вас думать». Теперь вы можете начать понимать, почему!
Дата: 2019-04-23, просмотров: 195.
