В математике мы можем использовать символы в уравнениях и формулах. Мы можем заменить эти символы различными числами, а уравнение все еще работают. Например, мы могли бы составить формулу для сложения двух чисел, используя символы: х + 1 = у.

Мы можем либо заменить x на число и решить уравнение для y, либо заменить y на число и решить для x.

Точно так же мы можем символизировать суждения в дедуктивных доказательствах и только с помощью символической формы мы можем лучше увидеть структуру этого доказательства.

Предположим, я хочу доказать, что люди принадлежат к классу объектов, которые являются рациональными и сознательными. Я могу записать такой аргумент:
Все люди рациональны
Все рациональные вещи сознательны
Поэтому все люди сознательны
Теперь запишем это с помощью символов. Пусть H обозначает человека, R обозначает рациональное, а C обозначает сознательное и записывает наш аргумент как:
Все H являются R
Все R являются C
Поэтому все H являются C

Обратите внимание, что мы также можем заменить H, C и R любым термином или символом, и это не изменит общую структуру аргумента.  Давайте заменим Н на «студенты», R на «образованными», С на «вежливыми». Получается

Все студенты являются образованными

Все образованные являются вежливыми
Поэтому все студенты являются вежливыми

Или замените H на «яблоко», R на «спелый» и C на «сумасшедший». Теперь у нас есть:

Все яблоки спелые
Все спелые вещи сумасшедшие
Поэтому все яблоки сумасшедшие

Аргумент бессмысленный, но он сохраняет ту же структуру, и мы увидим, почему это важно в дальнейшем.

Таким образом, используя символы, мы можем отделить структуру аргумента от его  содержимого, и это будет ключом к разбивке аргументов для анализа. Простые высказывания могут объединяться с другими простыми высказываниями и составлять структуру сложного высказывания.

Например: « Современные компьютерные системы - это машины Тьюринга, которые могут обрабатывать триллионы операций в секунду, хотя основные операции чрезвычайно просты: они, по сути, переходят из состояний от 1 до 4 или включаются, полу- включаются, частично включаются и выключаются.»

Сколько утверждений правды декларируется в этом предложении? Если бы вы хотели сформулировать единственное значение истинности всему утверждению, что бы это было? Если вам трудно разобраться, имеет смысл разбить данное высказывание на несколько простых:

1. Современные компьютерные системы - это машины Тьюринга. - Истина

2. И современные компьютеры могут обрабатывать триллионы операций в секунду. - Истина

3.  НО основные операции компьютерных систем предельно просты. - Истина

4. И современные компьютерные системы переходят из состояний от 1 до 4: включен, полу-включен, частично включен и выключен. – Ложь

Теперь легче увидеть все правдивые высказывания. Слова «И» и «НО» разделяют простые утверждения. И и НО помогают нам разделять простые утверждения и помогают объединять простые высказывания в составное высказывания. Мы можем легче управлять значением истинности каждого простого утверждения.

Все составные операторы, оперирующие с двумя простыми высказываниями, называются «функционально-истинными» составными операторами. Это означает, что значение истинности всего утверждения определяется значением истинности отдельных простых утверждений, которые его составляют, и функцией оператора в этих утверждениях.

Если вы пишете компьютерные программы, вы можете рассматривать простые выражения как входные данные, а оператор - как функцию, которая принимает эти входные данные и что-то с ними делает. Выход всей функции определяется значением входов и конкретной операцией функции. Рассмотрим простую программу, написанную в псевдокоде, которая изменит все строчные символы в строке на заглавные буквы, а затем выведет его на экран:

Если мы отправим строку «карандаш» в нашу функцию, она выведет «КАРАНДАШ» на экран. Здесь важно то, что вывод определяется как значением, которое мы передаем функции, так и операцией, которая выполняется для этого значения самой функцией.

Итак,

Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).

Логические операции (операторы) - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.

Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).

Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.

Оператор отрицания

Оператор отрицание – единственный оператор, который обрабатывает одно простое высказывание (монадический оператор). Если простое утверждение истинно, размещение перед ним (или над ним) символа отрицания делает составное утверждение ложным. Если простое утверждение ложно, но перед ним ставится отрицание, что делает сложное утверждение истинным.

Символ: ~ «высказывание» (тильда) или 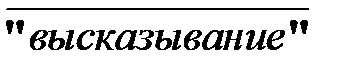(верхнее подчеркивание)

Пример:

Высказывание А –«Петр на лекции»

Отрицание - ~А – «Это не тот случай, когда Петр на лекции»

Очень важно, что бы простое высказывание не изменилось, а оператор оказался бы применен. Если сказать «Петр не на лекции» простое высказывание меняется. Поэтому с точки зрения применения оператора правильно использовать формулировку «Это не тот случай, когда Петр на лекции».