Механизмы транспортирования ткани швейных машин представляют собой рычажные механизмы достаточно сложной структуры. Для решения задач кинематического анализа подобных механизмов чаще всего используется ЭВМ, разрабатываются пакеты прикладных программ. Общих программ анализа кинематики рычажных механизмов произвольного вида не существует. Разработка таких программ является весьма сложной задачей, требующей от исследователя соответствующих математических моделей и алгоритмического обеспечения.

Настоящая глава посвящена обзору алгоритмического обеспечения решения задач кинематического анализа рычажных механизмов, применяемых для транспортирования ткани в швейных машинах. Для реечного транспортирующего механизма швейных машин на стадии кинематического анализа характерно решение следующих задач:

1) определение функций положения, первых и вторых передаточных функций обобщенных координат звеньев механизма от обобщенной координаты входного звена;

2) определение траектории движения заданных конструктором точек рабочего органа механизма – рейки;

3) определение величины шага транспортирования Т;

4) определение зависимости шага транспортирования Т от параметров регулирования длины стежка, предусмотренных кинематической схемой механизма;

5) нахождение предельных значений параметров регулирования соответствующих верхней и нижней границе изменения шага транспортирования.

Для дифференциальных транспортирующих механизмов, перемещение материала в которых происходит двумя зубчатыми рейками — основной и дополнительной, перечисленные задачи решаются для каждой рейки в отдельности и, кроме того, определяются: степень дифференцирования подачи m (отношение шага транспортирования дополнительной рейки к шагу транспортирования основной рейки); зависимость m от параметров регулирования, предусмотренных кинематической схемой механизма; граничные значения параметров регулирования.

В качестве аналитического метода описания математической модели для кинематического анализа таких сложных многозвенных рычажных механизмов, как реечные механизмы транспортирования ткани швейных машин, на наш взгляд наиболее применим метод погруппного анализа [4]. Суть его состоит в последовательном математическом описании структурных групп Ассура, входящих в состав механизма, в порядке их присоединения при образовании структурной схемы. Исходя из анализа структурных схем транспортирующих механизмов швейных машин, можно заключить, что в них, как правило, применяются двухповодковые структурные группы Ассура первой, второй и третьей модификаций, а также, различные модификации трехповодковых структурных групп. Алгоритм кинематического анализа реечного механизма транспортирования ткани, согласно методу погруппного анализа, представляет собой некоторый головной модуль, объединяющий отдельные модули, каждый из которых содержит алгоритм анализа соответствующей структурной группы Ассура, в порядке их присоединения друг к другу, начиная с входного звена.

Рассмотрим ниже математические модели и алгоритмы кинематического анализа структурных групп Ассура, наиболее часто встречающихся в схемах реечных механизмов транспортирования ткани швейных машин. При этом решение задачи кинематического анализа осуществляется на ЭВМ численно для ряда дискретных значений угла поворота a (обобщенной координаты) входного звена транспортирующего механизма. Дискретное значение угла a для i-го положения входного звена может быть, например, определено из выражения:

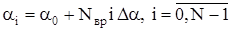,                                                       (1.1)

где a₀ – начальное значение угла a; Da - выбранный исследователем шаг изменения угла a; N_вр – коэффициент, характеризующий направление вращения: N_вр=+1 или –1 при вращении соответственно против или по часовой стрелке; N – количество рассчитываемых положений механизма (начальное положение механизма совпадает с нулевым), N=2p/Da. Величина a₀ представляет собой исходное значение угла a, выбираемое конструктором произвольно.