Рассмотрим плоскость, заданную общим уравнением Ах+ By + Cz + D =0, и прямую, заданную каноническим уравнением
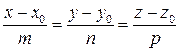 .
.
Т.к. угол j между прямой и плоскостью является дополнительным к углу x между направляющим вектором прямой 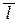 (m ; n ; p) и нормальным вектором плоскости
(m ; n ; p) и нормальным вектором плоскости 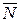 (A ; B ; C),
(A ; B ; C),

то из определения скалярного произведения 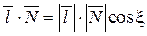 и равенства cosx=cos(90°-j)=sinj получим:
и равенства cosx=cos(90°-j)=sinj получим:
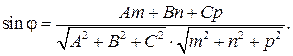
Условие параллельности прямой и плоскости
Условие параллельности прямой и плоскости эквивалентно условию перпендикулярности векторов 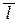 (m ; n ; p) и
(m ; n ; p) и 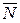 (A ; B ; C), и выражается равенством нулю скалярного произведения этих векторов:
(A ; B ; C), и выражается равенством нулю скалярного произведения этих векторов:
Am + Bn + Cp =0.
3.11.3. Условие перпендикулярности прямой и плоскости эквивалентно условию параллельности векторов 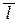 (m ; n ; p) и
(m ; n ; p) и 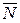 (A ; B ; C), и выражается пропорциональностью координат этих векторов:
(A ; B ; C), и выражается пропорциональностью координат этих векторов:
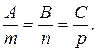
Кривые второго порядка
Эллипс
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2а.
 |
При этом не исключается совпадение фокусов эллипса, в этом случае получаем окружность.
Пусть точка М(х,у) – некоторая точка плоскости. Обозначим через r 1 и r 2 расстояния от точки М до точек F 1 и F 2 соответственно. Согласно определению эллипса равенство:
r 1 + r 2 =2 a
является необходимым и достаточным условием расположения точки М(х,у) на данном эллипсе.
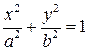 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Свойства эллипса.
1) Эллипс симметричен относительно осей Ох и Оу и точки О(0;0) – центра эллипса.
Точки пересечения эллипса с осями координат А1(а;0) и А2(-а;0), В1(0;b) и B2(0;- b) называются вершинами эллипса.
Отрезки А1А2=2а и В1B2=2 b называются соответственно большой и малой осями эллипса.
2) Эллипс содержится внутри прямоугольника | x | £ a, |y| £ b. В самом деле, из канонического уравнения вытекает, что 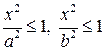 . Эти неравенства эквивалентны неравенствам | x | £ a, |y| £ b.
. Эти неравенства эквивалентны неравенствам | x | £ a, |y| £ b.
Отношение расстояния между фокусами к длине большой оси эллипса называется эксцентриситетом эллипса:
е=с/а.
Учитывая, что b 2 = a 2 - c 2, получим:
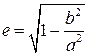 .
.
Из этой формулы видно, что эксцентриситет эллипса меньше единицы.
Чем больше эксцентриситет эллипса, тем меньше отношение 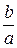 малой полуоси эллипса b к его большой полуоси а, и значит, тем более сплющенным будет эллипс.
малой полуоси эллипса b к его большой полуоси а, и значит, тем более сплющенным будет эллипс.
Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости F 1 и F 2, называемых фокусами, есть величина постоянная, равная 2а.
 |
Точки F 1 и F 2 имеют координаты F 1(c ,0) и F 2 (- c ,0).
Пусть точка М(х,у) – некоторая точка плоскости. Обозначим через r 1 и r 2 расстояния от точки М до точек F 1 и F 2 соответственно. Согласно определению гиперболы равенство:
| r 1 - r 2 |=2 a
является необходимым и достаточным условием расположения точки М(х,у) на данной гиперболе.
Уравнение гиперболы в данной системе координат примет вид:
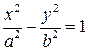 - каноническое уравнение гиперболы,
- каноническое уравнение гиперболы,
где b 2 = c 2 - a 2 .
Если а= b, то гипербола называется равносторонней.
Свойства гиперболы.
1) Гипербола симметрична относительно осей Ох и Оу и точки О(0;0) – центра гиперболы.
2) Гипербола состоит из двух частей, называемых ветвями гиперболы.
Точки пересечения гиперболы с осью Ох А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называется действительной осью гиперболы.
3) Прямые 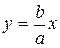 и
и 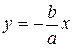 называются асимптотами гиперболы (ветви гиперболы неограниченно приближаются к этим прямым).
называются асимптотами гиперболы (ветви гиперболы неограниченно приближаются к этим прямым).
Отношение расстояния между фокусами к длине действительной оси эллипса называется эксцентриситетом гиперболы:
е=с/а.
Учитывая, что b 2 =с2-а2, получим:
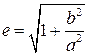 .
.
Из этой формулы видно, что эксцентриситет гиперболы больше единицы.
Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины угла между ее асимптотами, т.к. отношение 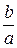 есть тангенс половины угла между асимптотами гиперболы.
есть тангенс половины угла между асимптотами гиперболы.
Парабола
Параболой называется множество точек плоскости, каждая из которых одинаково удалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.
Расстояние от фокуса F до директрисы l называется параметром параболы и обозначается через р.
Пусть ось Ох проходит через фокус F перпендикулярно директрисе, а начало координат расположено посередине между фокусом и директрисой. Тогда F(p /2;0), а уравнение директрисы х=-р\2.
у2=2рх
– каноническое уравнение параболы.
 |
Свойства параболы.
1) Парабола симметрична относительно оси Ох (Ох - ось симметрии параболы), т.к. в каноническом уравнении параболы величина у фигурирует в четной степени.
Парабола проходит через начало координат, точка О(0;0) – вершина параболы.
Отметим, что кривая у2=2рх при р<0 также является параболой, которая располагается в левой полуплоскости.
Пример расчетно-графической работы и образец ее выполнения.
Вариант №0
1. Вычислить произведение матриц
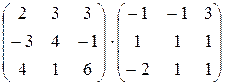 .
.
Вычислить определитель
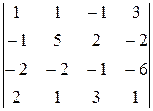 .
.
3. Найти обратную матрицу
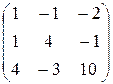 .
.
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
б) Методом Крамера.
в) Методом Гаусса.
а) 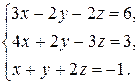 б)
б) 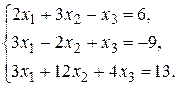 в)
в) 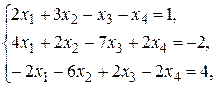
5. Написать разложение вектора 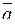 по базису
по базису 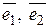 :
:
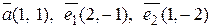 .
.
6. Установить, являются ли векторы 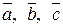 линейно-зависимыми:
линейно-зависимыми:
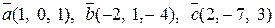 .
.
7. Найти площадь параллелограмма, построенного на векторах 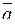 и
и 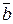 :
:
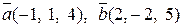 .
.
8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(3, 3) и найти расстояние от точки Р(1,-2) до полученной прямой.
9. Найти угол между прямыми:
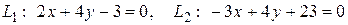 .
.
10. От общего уравнения прямой
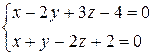
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
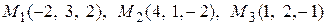 .
.
12. Найти расстояние от точки М до плоскости p:
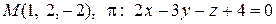 .
.
13. Найти проекцию точки М на плоскость p:
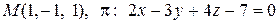 .
.
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
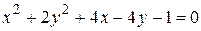 .
.
Решение варианта №0
1. Вычислить произведение матриц
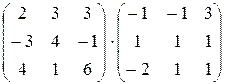 .
.
Решение:
Умножение матриц можно произвести только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы. В данном случае это условие выполняется, поэтому произведение матриц можно вычислить. По правилу умножения матриц «строка на столбец» находим
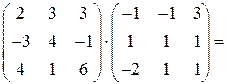
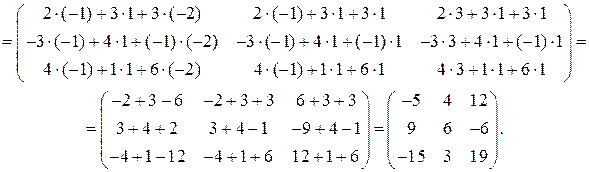
Ответ: 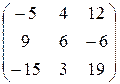 .
.
Вычислить определитель
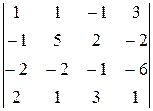 .
.
Решение:
Используя свойства определителей, обратим в нуль все, кроме одного, элементы его первого столбца. Для этого произведем следующие действия: 1) к элементам 2-ой строки прибавим элементы 1-ой строки, 2) к элементам 3-ей строки прибавим элементы 1-ой строки, умноженные на 2, 3) к элементам 4-ой строки прибавим элементы 1-ой строки, умноженные на -2.
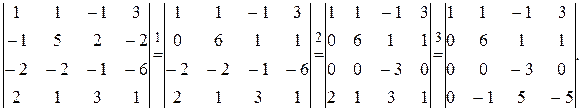
Полученный определитель разложим по элементам 1-го столбца: 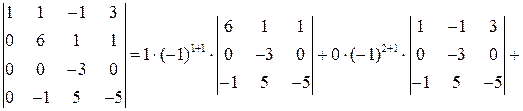
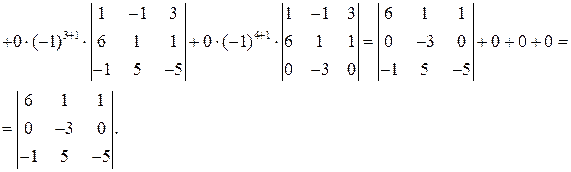
Теперь полученный определитель можно разложить по 2-ой строке (т.к. она содержит два нуля):
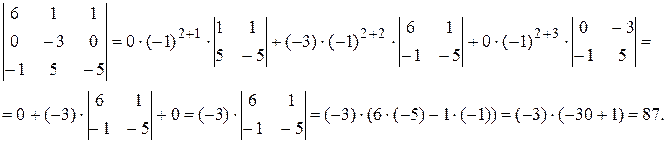
Ответ: 87.
3. Найти обратную матрицу
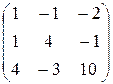 .
.
Решение:
Обратная матрица вычисляется по формуле:
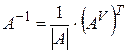 ,
,
где |А| - определитель исходной матрицы А, |А|¹0.
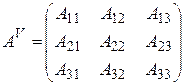 - матрица алгебраических дополнений для исходной матрицы А.
- матрица алгебраических дополнений для исходной матрицы А.
Вычислим определитель исходной матрицы по правилу «треугольников», он не должен быть равен 0.
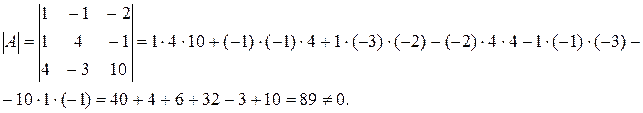
Вычислим алгебраические дополнения элементов исходной матрицы:
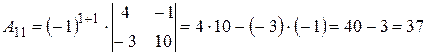 ,
,
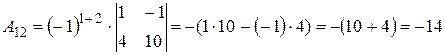 ,
,
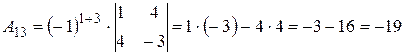 ,
,
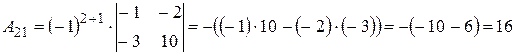 ,
,
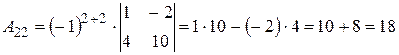 ,
,
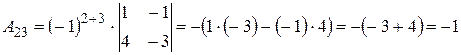 ,
,
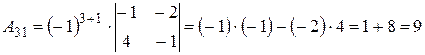 ,
,
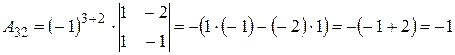 ,
,
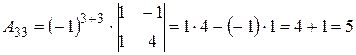 .
.
Составляем матрицу из алгебраических дополнений и транспонируем ее:
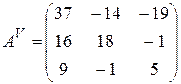 ,
, 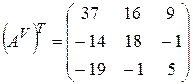 .
.
Подставляем полученные выражения в формулу:
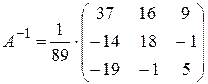 .
.
Ответ: 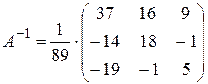
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
б) Методом Крамера.
в) Методом Гаусса.
а) 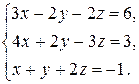 б)
б) 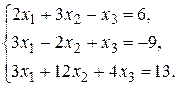 в)
в) 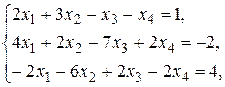
Решение:
а) Метод обратной матрицы.
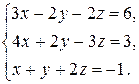
Решение ищется по формуле:
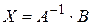 ,
,
где 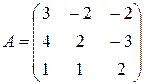 - матрица коэффициентов системы,
- матрица коэффициентов системы,
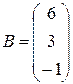 - столбец свободных членов.
- столбец свободных членов.
Найдем обратную матрицу для матрицы А:
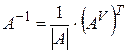 ,
,
где |А| - определитель исходной матрицы А, |А|¹0.
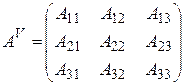 - матрица алгебраических дополнений для исходной матрицы А.
- матрица алгебраических дополнений для исходной матрицы А.
Вычислим определитель исходной матрицы по правилу «треугольников», он не должен быть равен 0.
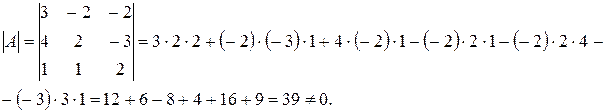
Вычислим алгебраические дополнения элементов исходной матрицы:
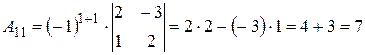 ,
,
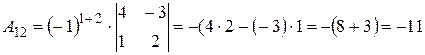 ,
,
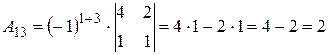 ,
,
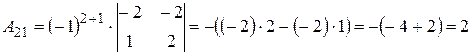 ,
,
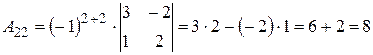 ,
,
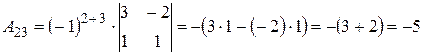 ,
,
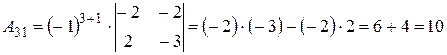 ,
,
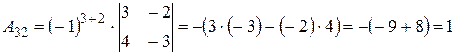 ,
,
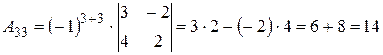 .
.
Составляем матрицу из алгебраических дополнений и транспонируем ее:
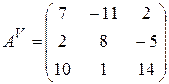 ,
, 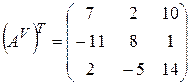 .
.
Затем подставляем полученные выражения в формулу:
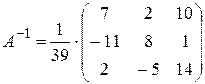 .
.
Теперь найдем X, вычислив произведение А-1×В:
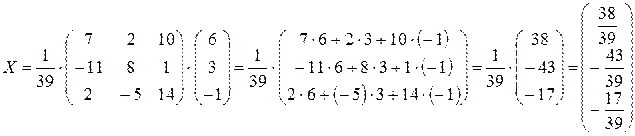 Таким образом, получим решение
Таким образом, получим решение 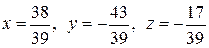 .
.
Ответ: 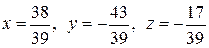 .
.
б) Метод Крамера.
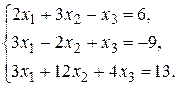
Если определитель системы D¹0, то решение системы можно найти по формулам Крамера:
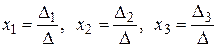 ,
,
где D1, D2, D3 – определители, полученные путем замены соответствующего столбца на столбец свободных членов.
Вычислим определители по правилу «треугольников»:
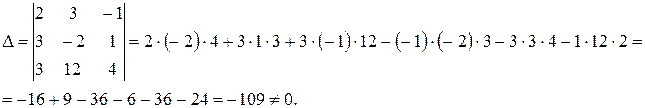
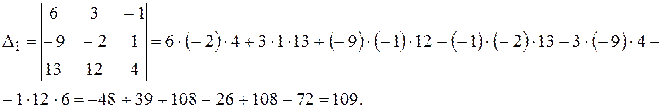
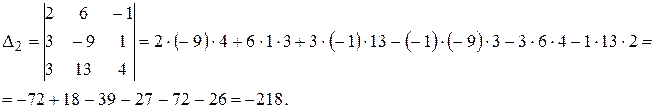
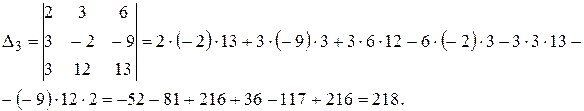
Подставляем полученные значения в формулы Крамера, и находим решения системы:
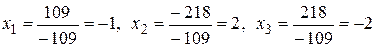 .
.
Ответ: 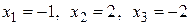 .
.
в) Метод Гаусса.
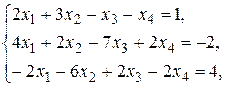
Составим расширенную матрицу коэффициентов системы:
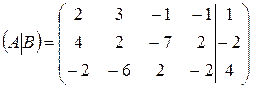 .
.
Приведем её путем элементарных преобразований к трапециевидному виду: 1) к элементам 2-ой строки прибавим элементы 1-ой строки, умноженные на -2, 2) к элементам 3-ей строки прибавим элементы 1-ой строки, 3) умножим элементы 3-ей строки на -4, 4) к элементам 3-ей строки прибавим элементы 2-ой строки, умноженные на 3.
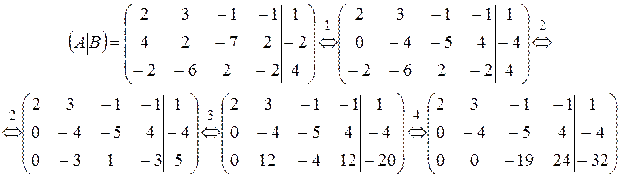
Ранг матрицы коэффициентов равен рангу расширенной матрицы, значит, система совместна. При этом ранг матрицы коэффициентов меньше числа неизвестных, поэтому система имеет множество решений.
Три неизвестных примем за базисные (т.к. ранг матрицы коэффициентов равен 3), одна неизвестная будет свободной.
Выделим минор третьего порядка, не равный нулю:
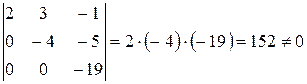
Тогда 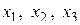 будут базисными переменными,
будут базисными переменными, 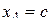 - свободной переменной.
- свободной переменной.
Составим систему уравнений, соответствующую полученной матрице:
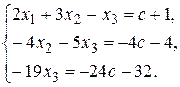
Теперь вычислим значения неизвестных.
Из третьего уравнения получаем х3:
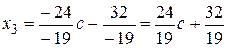 ,
,
Из второго уравнения находим х2:
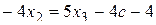 ,
, 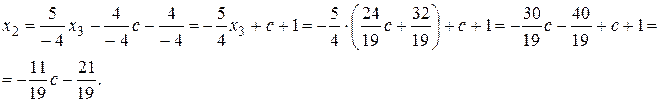 Из первого уравнения находим х1:
Из первого уравнения находим х1:
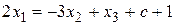 ,
,
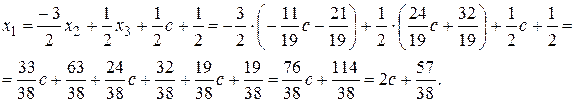
Ответ: 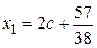 ,
, 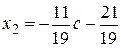 ,
, 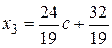 ,
, 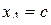 .
.
5. Написать разложение вектора 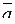 по базису
по базису 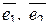 :
:
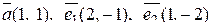 .
.
Решение:
Разложение вектора 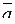 по базису
по базису 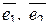 имеет вид:
имеет вид:
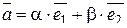 ,
,
где a и b - координаты вектора 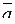 в данном базисе.
в данном базисе.
Подставим координаты векторов в указанное равенство:
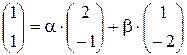 .
.
Получим систему уравнений для определения координат вектора 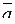 :
:
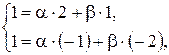
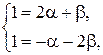
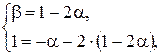
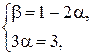
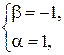
Получаем следующее разложение по базису для вектора 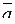 :
:
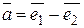 .
.
Ответ: 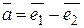 .
.
6. Установить, являются ли векторы 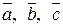 линейно-зависимыми:
линейно-зависимыми:
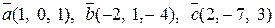 .
.
Решение:
Векторы 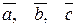 являются линейно зависимыми, если их смешанное произведение равно нулю, и являются линейно независимыми, если их смешанное произведение не равно нулю.
являются линейно зависимыми, если их смешанное произведение равно нулю, и являются линейно независимыми, если их смешанное произведение не равно нулю.
Вычислим смешанное произведение данных векторов в координатной форме:
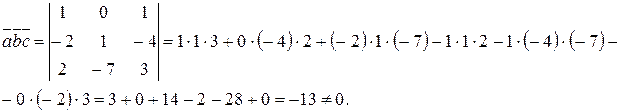
Таким образом, векторы 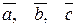 линейно независимы.
линейно независимы.
Ответ: векторы линейно независимы.
7. Найти площадь параллелограмма, построенного на векторах
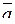 и
и 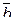 :
: 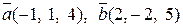 .
.
Решение:
Площадь параллелограмма, построенного на векторах 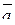 и
и 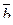 , численно равна модулю векторного произведения данных векторов, и вычисляется по формуле:
, численно равна модулю векторного произведения данных векторов, и вычисляется по формуле:
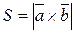 .
.
Найдем векторное произведение данных векторов, вычисляя определитель разложением по элементам 1-го столбца:
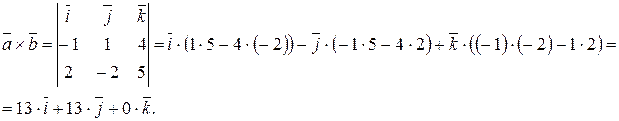
Найдем площадь искомого параллелограмма, вычислив модуль вектора 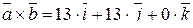 :
:
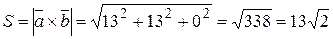 .
.
Ответ: 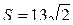 .
.
8. Составить уравнение прямой, проходящей через две точки М1(1,5), М2(3,3) и найти расстояние от точки Р(1,-2) до полученной прямой.
Решение:
Уравнение прямой, проходящей через две точки М1(х1,у1) и М2(х2,у2), записывается в виде:
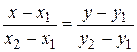 .
.
В данном случае имеем 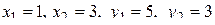 , подставим эти значения в уравнение:
, подставим эти значения в уравнение:
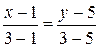 ,
,
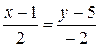 ,
,
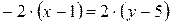 ,
,
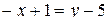 ,
,
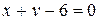 .
.
Получили общее уравнение прямой, проходящей через две данные точки М1(1,5), М2(3,3).
Найдем расстояние от точки Р(1,-2) до полученной прямой.
Расстояние от точки Р(х0,у0) до прямой Ах+Ву+С=0 находится по формуле:
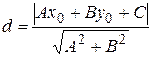 .
.
В данном случае 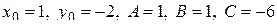 . Подставляем эти значения в формулу:
. Подставляем эти значения в формулу:
 .
.
Ответ: 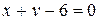 ,
, 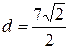 .
.
9. Найти угол между прямыми:
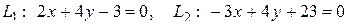 .
.
Решение:
Угол между прямыми равен углу между их нормальными векторами.
Косинус угла между векторами можно вычислить по формуле:
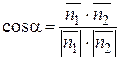 ,
,
где 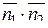 - скалярное произведение векторов
- скалярное произведение векторов 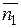 и
и 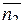 ,
,
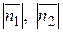 - модули векторов
- модули векторов 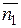 и
и 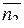 .
.
Если прямая задана общим уравнением Ах+Ву+С=0, то ее нормальный вектор имеет координаты 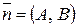 . Поэтому для прямой
. Поэтому для прямой 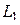 нормальный вектор будет иметь вид
нормальный вектор будет иметь вид 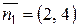 , для прямой
, для прямой 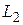 нормальный вектор будет иметь вид
нормальный вектор будет иметь вид 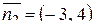 .
.
Найдем скалярное произведение данных векторов в координатной форме:

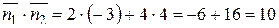 .
.
Теперь вычислим модули данных векторов:
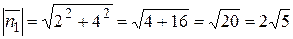 ,
,
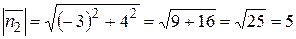 .
.
Вычисляем косинус угла между нормальными векторами прямых:
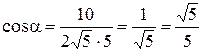 .
.
Отсюда искомый угол между прямыми будет равен:
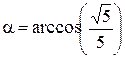 .
.
Ответ: 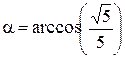 .
.
10. От общего уравнения прямой
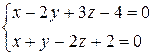
перейти к каноническому уравнению.
Решение:
Каноническое уравнение прямой имеет вид:
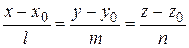 ,
,
где 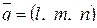 - направляющий вектор данной прямой,
- направляющий вектор данной прямой,
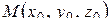 - точка, принадлежащая прямой.
- точка, принадлежащая прямой.
Направляющий вектор прямой 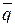 – это вектор, параллельный данной прямой, поэтому он должен быть перпендикулярен нормальным векторам плоскостей, определяющих данную прямую,
– это вектор, параллельный данной прямой, поэтому он должен быть перпендикулярен нормальным векторам плоскостей, определяющих данную прямую, 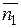 и
и 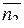 . Тогда должно выполняться соотношение:
. Тогда должно выполняться соотношение:
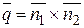 ,
,
где 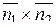 - векторное произведение векторов
- векторное произведение векторов 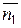 и
и 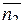 .
.
Найдем по уравнениям плоскостей координаты их нормальных векторов:
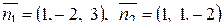 .
.
Найдем вектор 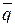 :
:
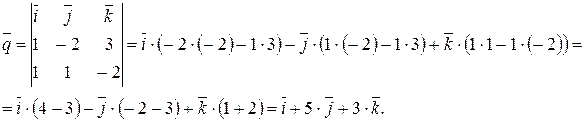
Поэтому вектор 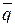 имеет координаты
имеет координаты 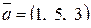 .
.
В качестве точки 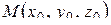 , через которую проходит искомая прямая, можно взять точку пересечения ее с любой из координатных плоскостей, например с плоскостью Oyz. Так как при этом
, через которую проходит искомая прямая, можно взять точку пересечения ее с любой из координатных плоскостей, например с плоскостью Oyz. Так как при этом 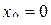 , то координаты
, то координаты 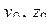 этой точки определятся из системы уравнений заданных плоскостей, если в них положить
этой точки определятся из системы уравнений заданных плоскостей, если в них положить 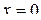 :
:
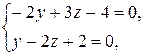
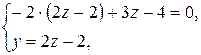
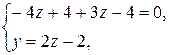
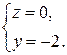
Получаем координаты точки 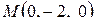 .
.
Подставляем координаты точки М и направляющего вектора 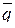 в каноническое уравнение системы:
в каноническое уравнение системы:
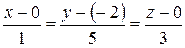 ,
,
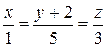 .
.
Ответ: 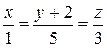 .
.
11. Написать уравнение плоскости, проходящей через три заданные точки
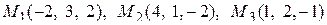 .
.
Решение:
Уравнение плоскости, проходящей через точки 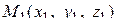 ,
, 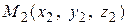 ,
, 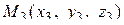 , имеет вид:
, имеет вид:
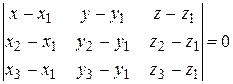 .
.
Подставим координаты точек в уравнение:
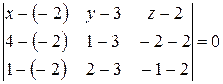 ,
,
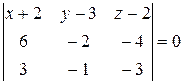 .
.
Вычислим определитель слева разложением по элементам первой строки:
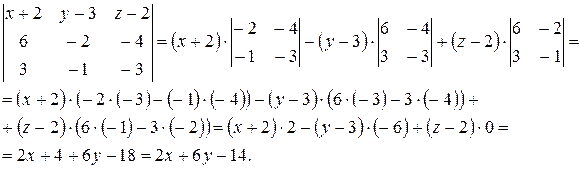
Получаем уравнение искомой плоскости:
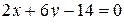 ,
,
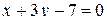 .
.
Ответ: 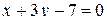 .
.
12. Найти расстояние от точки М до плоскости p:
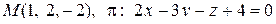 .
.
Решение:
Расстояние от точки 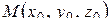 до плоскости Ах+Ву+С z + D=0 вычисляется по формуле:
до плоскости Ах+Ву+С z + D=0 вычисляется по формуле:
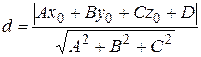 .
.
В нашем случае 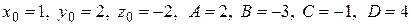 . Подставляем эти значения в формулу и получаем:
. Подставляем эти значения в формулу и получаем:
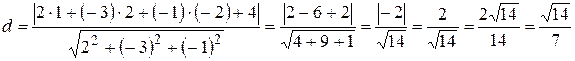 .
.
Ответ: 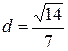 .
.
13. Найти проекцию точки М на плоскость p:
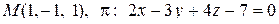 .
.
Решение:
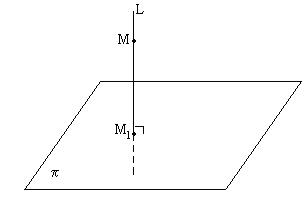
Составим уравнение прямой L, проходящей через точку M перпендикулярно плоскости p, тогда искомая проекция есть точка пересечения прямой 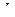 и плоскости p.
и плоскости p.
Из общего уравнения плоскости определим нормальный вектор 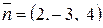 , он перпендикулярен плоскости и, значит, параллелен прямой L, т.е. является направляющим вектором для прямой L:
, он перпендикулярен плоскости и, значит, параллелен прямой L, т.е. является направляющим вектором для прямой L: 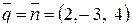 .
.
Уравнение прямой, проходящей через точку 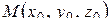 и имеющей направляющий вектор
и имеющей направляющий вектор 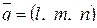 имеет вид:
имеет вид:
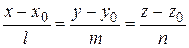 .
.
В нашем случае для точки 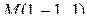 и вектора
и вектора 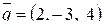 получаем:
получаем:
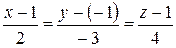 ,
,
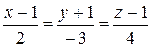 .
.
Найдем точку пересечения прямой и плоскости. Для этого запишем уравнение прямой в параметрическом виде:
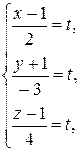
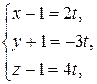
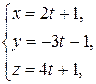
Подставим полученные выражения для x, y, z в уравнение плоскости:
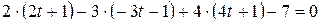 ,
,
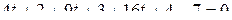 ,
,
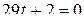 ,
,
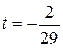 .
.
Подставим полученное значение t в параметрическое уравнение прямой, и, тем самым, найдем координаты точки М1 пересечения прямой L и плоскости p, т.е. координаты проекции точки М на плоскость p:
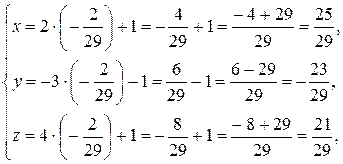
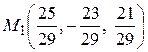 .
.
Ответ: 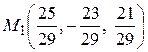 .
.
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
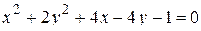 .
.
Решение:
Выделим в правой части уравнения полные квадраты относительно х и у:
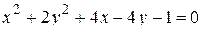 ,
,
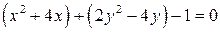 ,
,
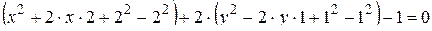 ,
,
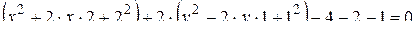 ,
,
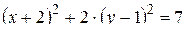 ,
,
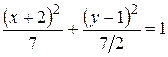 .
.
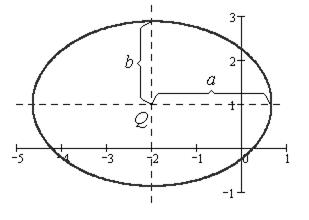
Получили каноническое уравнение эллипса с центром в точке Q 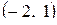 и полуосями
и полуосями 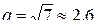 и
и 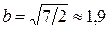 .
.
Построим эллипс с данными параметрами.
Работа выполняется в печатном виде на листах формата А4 с одной стороны листа. Правила оформления: https://narfu.ru/upload/medialibrary/1d0/Pravila_oformlenia_rabot_34_2018.pdf
Вариант определяется порядковым номером студента в журнале группы. Титульный лист распечатать с сайта САФУ. Второй лист РГР – это лист для замечаний, третий лист – лист заданий.
|
|
Вариант 1
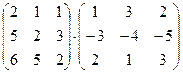 .
2. Вычислить определитель
.
2. Вычислить определитель
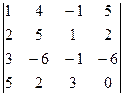 .
3. Найти обратную матрицу
.
3. Найти обратную матрицу
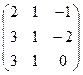 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
.
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
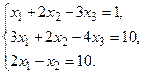 б) Методом Крамера.
б) Методом Крамера.
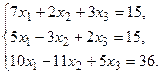 в) Методом Гаусса.
в) Методом Гаусса.
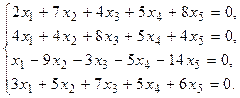 5. Написать разложение вектора
5. Написать разложение вектора 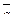 по базису
по базису 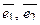 :
:
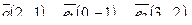
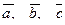 линейно-зависимыми:
линейно-зависимыми:
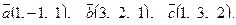 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 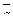 и
и 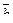 :
:
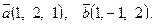 8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3, 4) и найти расстояние от точки P(0, 2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3, 4) и найти расстояние от точки P(0, 2) до полученной прямой.
9. Найти угол между прямыми
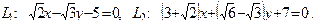 10. От общего уравнения прямой
10. От общего уравнения прямой
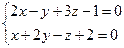 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
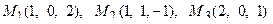 .
12. Найти расстояние от точки М до плоскости p:
.
12. Найти расстояние от точки М до плоскости p:
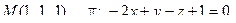 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
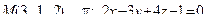 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
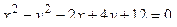
|
Вариант 2 | |
1. Вычислить произведение матриц
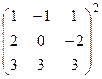 .
2. Вычислить определитель .
2. Вычислить определитель
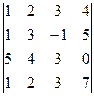 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
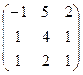 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
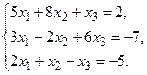 б) Методом Крамера.
б) Методом Крамера.
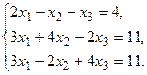 в) Методом Гаусса.
в) Методом Гаусса.
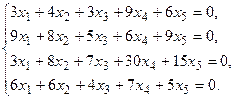 5. Написать разложение вектора
5. Написать разложение вектора 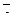 по базису по базису 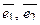 : :
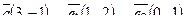
| 6. Установить, являются ли векторы 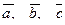 линейно-зависимыми: линейно-зависимыми:
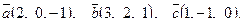 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 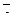 и и 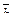 : :
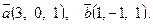 8. Составить уравнение прямой, проходящей через две точки М1(1,-2), М2(-2, 2) и найти расстояние от точки Р(3, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1,-2), М2(-2, 2) и найти расстояние от точки Р(3, 1) до полученной прямой.
9. Найти угол между прямыми
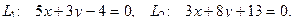 10. От общего уравнения прямой
10. От общего уравнения прямой
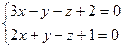 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
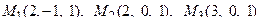 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
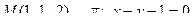 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
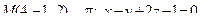 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
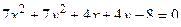
|
|
Вариант 3 | |
1. Вычислить произведение матриц
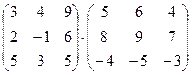 .
2. Вычислить определитель .
2. Вычислить определитель
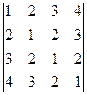 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
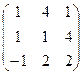 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
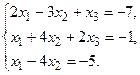 б) Методом Крамера.
б) Методом Крамера.
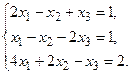 в) Методом Гаусса.
в) Методом Гаусса.
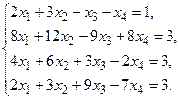 5. Написать разложение вектора
5. Написать разложение вектора 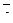 по базису по базису 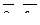 : :
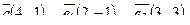
| 6. Установить, являются ли векторы 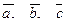 линейно-зависимыми: линейно-зависимыми:
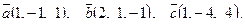 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 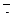 и и 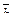 : :
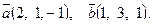 8. Составить уравнение прямой, проходящей через две точки М1(-2,-2), М2(0, 4) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(-2,-2), М2(0, 4) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
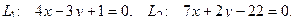 10. От общего уравнения прямой
10. От общего уравнения прямой
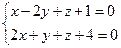 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
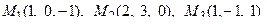 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
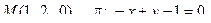 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
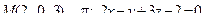 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
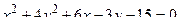 . .
|
|
Вариант 4 | |
1. Вычислить произведение матриц
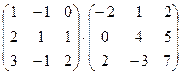 .
2. Вычислить определитель .
2. Вычислить определитель
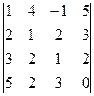 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
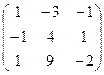 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
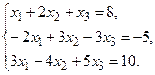 б) Методом Крамера.
б) Методом Крамера.
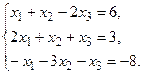 в) Методом Гаусса.
в) Методом Гаусса.
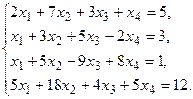 5. Написать разложение вектора
5. Написать разложение вектора 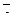 по базису по базису 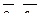 : :
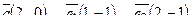
| 6. Установить, являются ли векторы 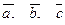 линейно-зависимыми: линейно-зависимыми:
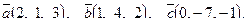 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 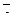 и и 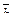 : :
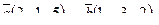 8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(5, 4) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(5, 4) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой 10. От общего уравнения прямой 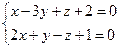 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
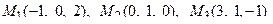 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
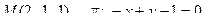 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
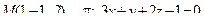 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
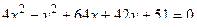 . .
|
|
Вариант 5 | |
1. Вычислить произведение матриц
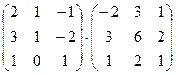 .
2. Вычислить определитель .
2. Вычислить определитель
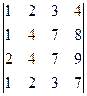 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
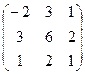 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
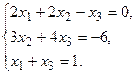 б) Методом Крамера.
б) Методом Крамера.
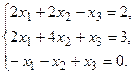 в) Методом Гаусса.
в) Методом Гаусса.
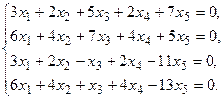 5. Написать разложение вектора
5. Написать разложение вектора 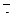 по базису по базису 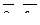 : :
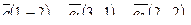
| 6. Установить, являются ли векторы 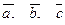 линейно-зависимыми: линейно-зависимыми:
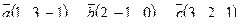 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 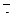 и и 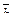 : :
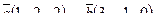 8. Составить уравнение прямой, проходящей через две точки М1(2,-2), М2(0, 3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2,-2), М2(0, 3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
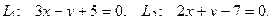 10. От общего уравнения прямой
10. От общего уравнения прямой
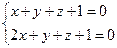 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
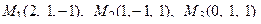 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
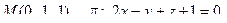 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
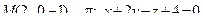 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
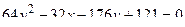 . .
|
|
Вариант 6 | |
1. Вычислить произведение матриц
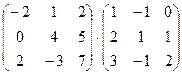 .
2. Вычислить определитель .
2. Вычислить определитель
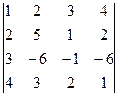 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
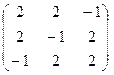 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
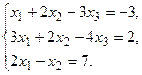 б) Методом Крамера.
б) Методом Крамера.
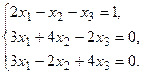 в) Методом Гаусса.
в) Методом Гаусса.
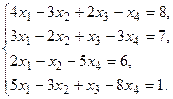 5. Написать разложение вектора
5. Написать разложение вектора 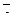 по базису по базису 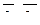 : :
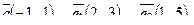
| 6. Установить, являются ли векторы 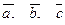 линейно-зависимыми: линейно-зависимыми:
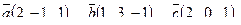 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах 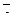 и и 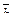 : :
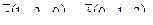 8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(1,-3) и найти расстояние от точки Р(-1, 0) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(1,-3) и найти расстояние от точки Р(-1, 0) до полученной прямой.
9. Найти угол между прямыми
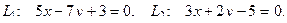 10. От общего уравнения прямой
10. От общего уравнения прямой
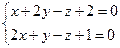 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
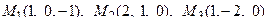 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
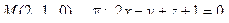 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
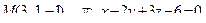 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
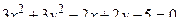 . .
|
|
Вариант 7 | |
1. Вычислить произведение матриц
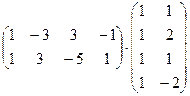 .
2. Вычислить определитель .
2. Вычислить определитель
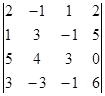 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
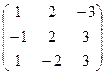 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
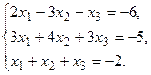 б) Методом Крамера.
б) Методом Крамера.
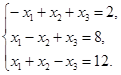 в) Методом Гаусса.
в) Методом Гаусса.
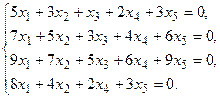 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 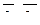 : :
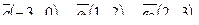
| 6. Установить, являются ли векторы 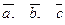 линейно-зависимыми: линейно-зависимыми:
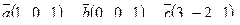 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 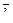 : :
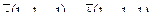 8. Составить уравнение прямой, проходящей через две точки М1(4,-2), М2(2,-3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(4,-2), М2(2,-3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
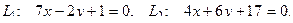 10. От общего уравнения прямой
10. От общего уравнения прямой
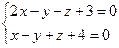 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
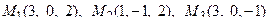 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
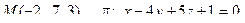 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
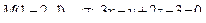 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
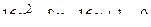 . .
|
|
Вариант 8 | |
1. Вычислить произведение матриц
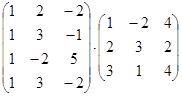 .
2. Вычислить определитель .
2. Вычислить определитель
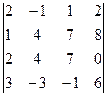 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
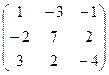 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
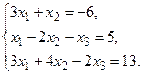 б) Методом Крамера.
б) Методом Крамера.
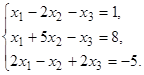 в) Методом Гаусса.
в) Методом Гаусса.
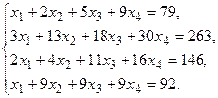 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 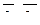 : :
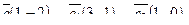
| 6. Установить, являются ли векторы 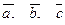 линейно-зависимыми: линейно-зависимыми:
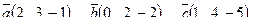 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 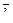 : :
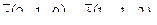 8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
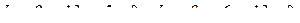 10. От общего уравнения прямой
10. От общего уравнения прямой
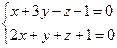 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
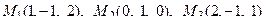 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
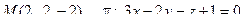 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
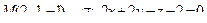 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
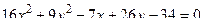 . .
|
|
Вариант 9 | |
1. Вычислить произведение матриц
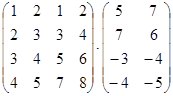 .
2. Вычислить определитель .
2. Вычислить определитель
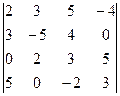 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
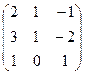 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
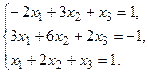 б) Методом Крамера.
б) Методом Крамера.
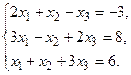 в) Методом Гаусса.
в) Методом Гаусса.
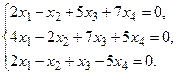 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 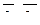 : :
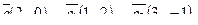
| 6. Установить, являются ли векторы 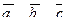 линейно-зависимыми: линейно-зависимыми:
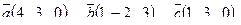 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 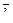 : :
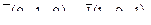 8. Составить уравнение прямой, проходящей через две точки М1(2, 5), М2(-2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2, 5), М2(-2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
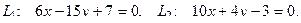 10. От общего уравнения прямой
10. От общего уравнения прямой
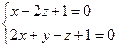 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
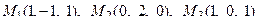 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
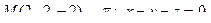 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
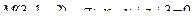 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
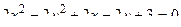 . .
|
|
Вариант 10 | |
1. Вычислить произведение матриц
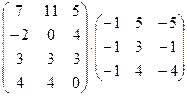 .
2. Вычислить определитель .
2. Вычислить определитель
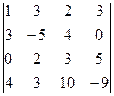 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
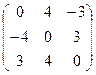 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
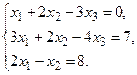 б) Методом Крамера.
б) Методом Крамера.
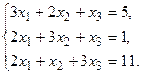 в) Методом Гаусса.
в) Методом Гаусса.
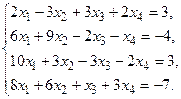 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 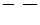 : :
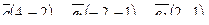
| 6. Установить, являются ли векторы 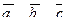 линейно-зависимыми: линейно-зависимыми:
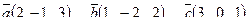 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 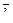 : :
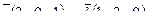 8. Составить уравнение прямой, проходящей через две точки М1(0, 5), М2(-2, 2) и найти расстояние от точки Р(2, 0) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(0, 5), М2(-2, 2) и найти расстояние от точки Р(2, 0) до полученной прямой.
9. Найти угол между прямыми
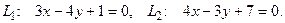 10. От общего уравнения прямой
10. От общего уравнения прямой
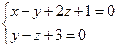 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
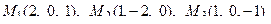 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
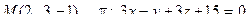 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
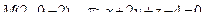 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
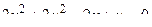 . .
|
|
Вариант 11 | |
1. Вычислить произведение матриц
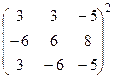 .
2. Вычислить определитель .
2. Вычислить определитель
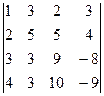 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
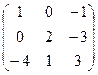 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
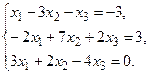 б) Методом Крамера.
б) Методом Крамера.
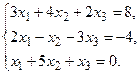 в) Методом Гаусса.
в) Методом Гаусса.
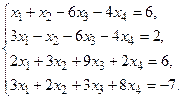 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 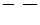 : :
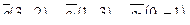
| 6. Установить, являются ли векторы 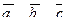 линейно-зависимыми: линейно-зависимыми:
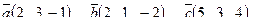 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 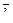 : :
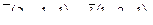 8. Составить уравнение прямой, проходящей через две точки М1(1, 0), М2(2, -3) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1, 0), М2(2, -3) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
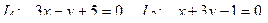 10. От общего уравнения прямой
10. От общего уравнения прямой
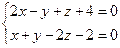 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
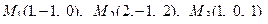 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
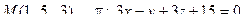 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
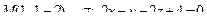 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
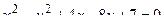 . .
|
|
Вариант 12 | |
1. Вычислить произведение матриц
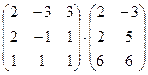 .
2. Вычислить определитель .
2. Вычислить определитель
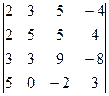 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
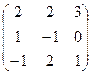 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
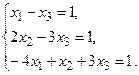 б) Методом Крамера.
б) Методом Крамера.
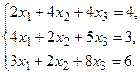 в) Методом Гаусса.
в) Методом Гаусса.
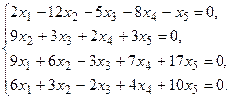 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 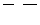 : :
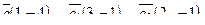
| 6. Установить, являются ли векторы 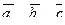 линейно-зависимыми: линейно-зависимыми:
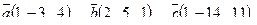 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 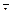 : :
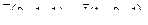 8. Составить уравнение прямой, проходящей через две точки М1(3, 3), М2(4, 2) и найти расстояние от точки Р(1,-4) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3, 3), М2(4, 2) и найти расстояние от точки Р(1,-4) до полученной прямой.
9. Найти угол между прямыми
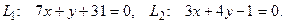 10. От общего уравнения прямой
10. От общего уравнения прямой
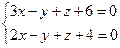 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
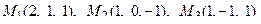 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
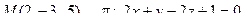 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
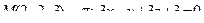 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
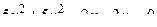 . .
|
|
Вариант 13 | |
1. Вычислить произведение матриц
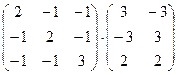 .
2. Вычислить определитель .
2. Вычислить определитель
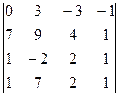 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
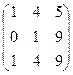 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
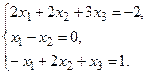 б) Методом Крамера.
б) Методом Крамера.
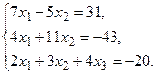 в) Методом Гаусса.
в) Методом Гаусса.
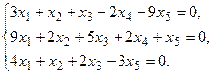 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 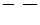 : :
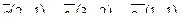
| 6. Установить, являются ли векторы 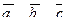 линейно-зависимыми: линейно-зависимыми:
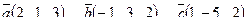 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 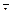 : :
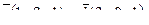 8. Составить уравнение прямой, проходящей через две точки М1(2, 2), М2(-6, 6) и найти расстояние от точки Р(3,-7) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2, 2), М2(-6, 6) и найти расстояние от точки Р(3,-7) до полученной прямой.
9. Найти угол между прямыми
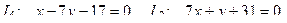 10. От общего уравнения прямой
10. От общего уравнения прямой
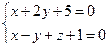 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
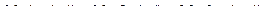 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
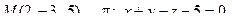 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
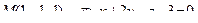 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
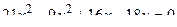 . .
|
|
Вариант 14 | |
1. Вычислить произведение матриц
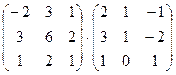 .
2. Вычислить определитель .
2. Вычислить определитель
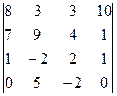 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
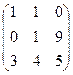 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
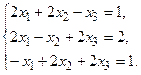 б) Методом Крамера.
б) Методом Крамера.
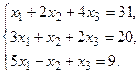 в) Методом Гаусса.
в) Методом Гаусса.
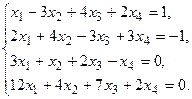 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 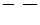 : :
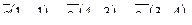
| 6. Установить, являются ли векторы 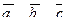 линейно-зависимыми: линейно-зависимыми:
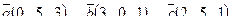 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 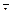 : :
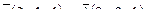 8. Составить уравнение прямой, проходящей через две точки М1(5, 2), М2(-6, 0) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(5, 2), М2(-6, 0) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
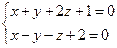 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
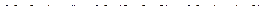 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
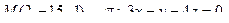 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
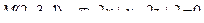 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
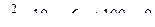 . .
|
|
Вариант 15 | |
1. Вычислить произведение матриц
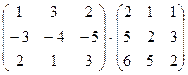 .
2. Вычислить определитель .
2. Вычислить определитель
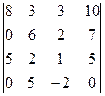 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
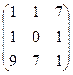 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
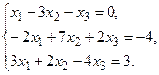 б) Методом Крамера.
б) Методом Крамера.
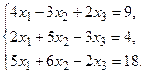 в) Методом Гаусса.
в) Методом Гаусса.
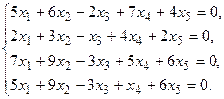 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису  : :
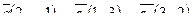
| 6. Установить, являются ли векторы 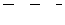 линейно-зависимыми: линейно-зависимыми:
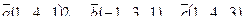 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 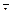 : :
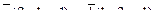 8. Составить уравнение прямой, проходящей через две точки М1(3, 2), М2(-3, 0) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3, 2), М2(-3, 0) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
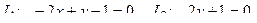 10. От общего уравнения прямой
10. От общего уравнения прямой
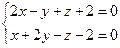 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
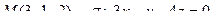 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
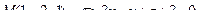 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
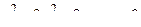 . .
|
|
Вариант 16 | |
1. Вычислить произведение матриц
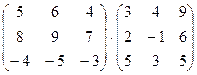 .
2. Вычислить определитель .
2. Вычислить определитель
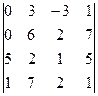 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
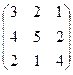 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
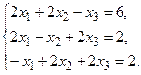 б) Методом Крамера.
б) Методом Крамера.
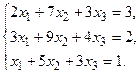 в) Методом Гаусса.
в) Методом Гаусса.
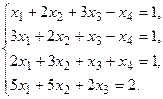 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 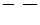 : :
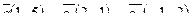
| 6. Установить, являются ли векторы 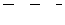 линейно-зависимыми: линейно-зависимыми:
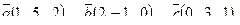 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
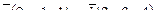 8. Составить уравнение прямой, проходящей через две точки М1(0, 2), М2(-3, 0) и найти расстояние от точки Р(-1, 2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(0, 2), М2(-3, 0) и найти расстояние от точки Р(-1, 2) до полученной прямой.
9. Найти угол между прямыми
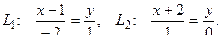 10. От общего уравнения прямой
10. От общего уравнения прямой
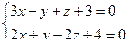 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
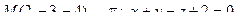 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
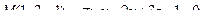 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
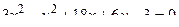 . .
|
|
Вариант 17 | |
1. Вычислить произведение матриц
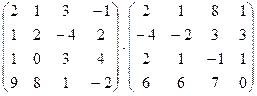 .
2. Вычислить определитель .
2. Вычислить определитель
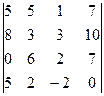 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
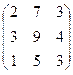 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
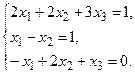 б) Методом Крамера.
б) Методом Крамера.
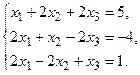 в) Методом Гаусса.
в) Методом Гаусса.
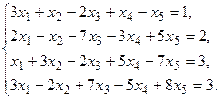 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 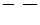 : :
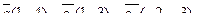
| 6. Установить, являются ли векторы 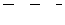 линейно-зависимыми: линейно-зависимыми:
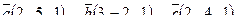 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
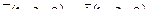 8. Составить уравнение прямой, проходящей через две точки М1(5, 2), М2(-3, 0) и найти расстояние от точки Р(-2, 2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(5, 2), М2(-3, 0) и найти расстояние от точки Р(-2, 2) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
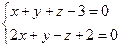 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
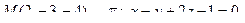 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
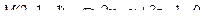 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
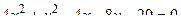 . .
|
|
Вариант 18 | |
1. Вычислить произведение матриц
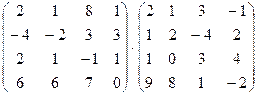 .
2. Вычислить определитель .
2. Вычислить определитель
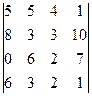 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
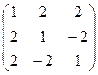 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
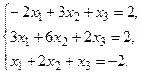 б) Методом Крамера.
б) Методом Крамера.
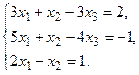 в) Методом Гаусса.
в) Методом Гаусса.
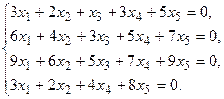 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису  : :
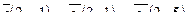
| 6. Установить, являются ли векторы 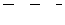 линейно-зависимыми: линейно-зависимыми:
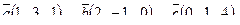 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
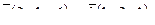 8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3,-5) и найти расстояние от точки Р(1,-2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3,-5) и найти расстояние от точки Р(1,-2) до полученной прямой.
9. Найти угол между прямыми
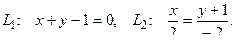 10. От общего уравнения прямой
10. От общего уравнения прямой
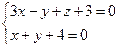 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
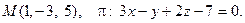 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
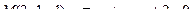 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
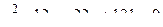 . .
|
|
Вариант 19 | |
1. Вычислить произведение матриц
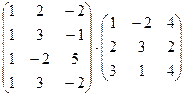 .
2. Вычислить определитель .
2. Вычислить определитель
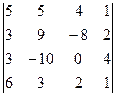 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
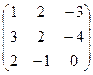 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
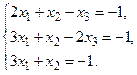 б) Методом Крамера.
б) Методом Крамера.
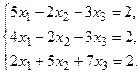 в) Методом Гаусса.
в) Методом Гаусса.
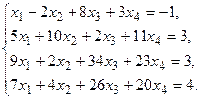 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 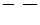 : :
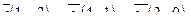
| 6. Установить, являются ли векторы 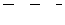 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(7,-3), М2(3,-5) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(7,-3), М2(3,-5) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
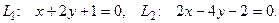 10. От общего уравнения прямой
10. От общего уравнения прямой
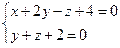 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
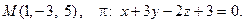 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
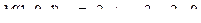 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
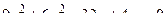 . .
|
|
Вариант 20 | |
1. Вычислить произведение матриц
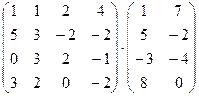 .
2. Вычислить определитель .
2. Вычислить определитель
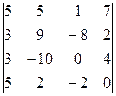 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
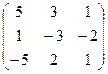 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
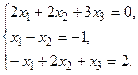 б) Методом Крамера.
б) Методом Крамера.
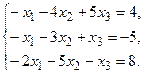 в) Методом Гаусса.
в) Методом Гаусса.
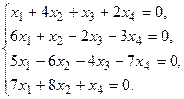 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 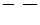 : :
| 6. Установить, являются ли векторы 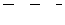 линейно-зависимыми: линейно-зависимыми:
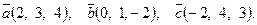 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
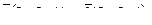 8. Составить уравнение прямой, проходящей через две точки М1(4, 3), М2(2, -3) и найти расстояние от точки Р(0, 3) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(4, 3), М2(2, -3) и найти расстояние от точки Р(0, 3) до полученной прямой.
9. Найти угол между прямыми
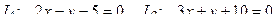 10. От общего уравнения прямой
10. От общего уравнения прямой
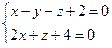 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
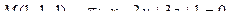 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
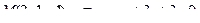 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
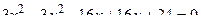 . .
|
|
Вариант 21 | |
1. Вычислить произведение матриц
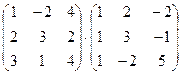 .
2. Вычислить определитель .
2. Вычислить определитель
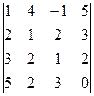 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
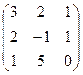 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
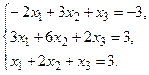 б) Методом Крамера.
б) Методом Крамера.
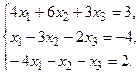 в) Методом Гаусса.
в) Методом Гаусса.
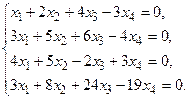 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 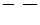 : :
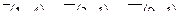
| 6. Установить, являются ли векторы 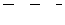 линейно-зависимыми: линейно-зависимыми:
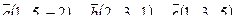 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 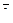 : :
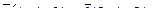 8. Составить уравнение прямой, проходящей через две точки М1(2, 6), М2(0, 7) и найти расстояние от точки Р(1, 0) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2, 6), М2(0, 7) и найти расстояние от точки Р(1, 0) до полученной прямой.
9. Найти угол между прямыми
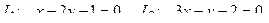 10. От общего уравнения прямой
10. От общего уравнения прямой
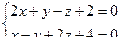 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
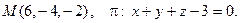 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
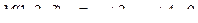 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
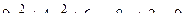 . .
|
|
Вариант 22 | |
1. Вычислить произведение матриц
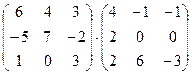 .
2. Вычислить определитель .
2. Вычислить определитель
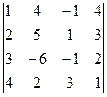 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
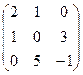 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
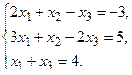 б) Методом Крамера.
б) Методом Крамера.
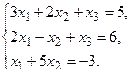 в) Методом Гаусса.
в) Методом Гаусса.
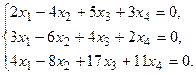 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису  : :
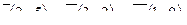
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 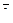 : :
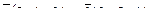 8. Составить уравнение прямой, проходящей через две точки М1(5, 5), М2(0, 2) и найти расстояние от точки Р(-1,-3) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(5, 5), М2(0, 2) и найти расстояние от точки Р(-1,-3) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
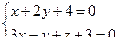 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
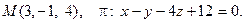 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
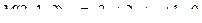 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
|
Вариант 23 | |
1. Вычислить произведение матриц
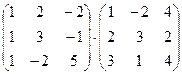 .
2. Вычислить определитель .
2. Вычислить определитель
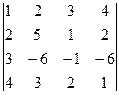 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
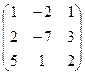 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
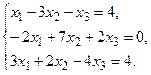 б) Методом Крамера.
б) Методом Крамера.
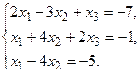 в) Методом Гаусса.
в) Методом Гаусса.
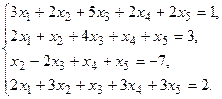 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 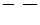 : :
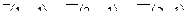
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
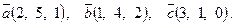 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 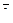 : :
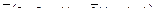 8. Составить уравнение прямой, проходящей через две точки М1(3, 3), М2(2, 0) и найти расстояние от точки Р(-1, 2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3, 3), М2(2, 0) и найти расстояние от точки Р(-1, 2) до полученной прямой.
9. Найти угол между прямыми
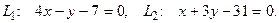 10. От общего уравнения прямой
10. От общего уравнения прямой
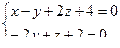 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
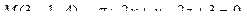 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
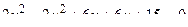 . .
|
|
Вариант 24 | |
1. Вычислить произведение матриц
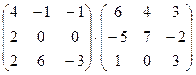 .
2. Вычислить определитель .
2. Вычислить определитель
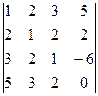 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
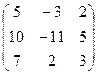 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
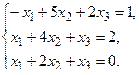 б) Методом Крамера.
б) Методом Крамера.
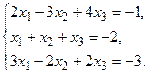 в) Методом Гаусса.
в) Методом Гаусса.
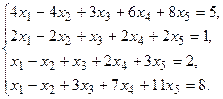 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису  : :
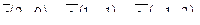
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
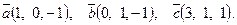 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 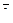 : :
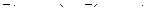 8. Составить уравнение прямой, проходящей через две точки М1(3, 0), М2(2,-1) и найти расстояние от точки Р(-2, 4) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3, 0), М2(2,-1) и найти расстояние от точки Р(-2, 4) до полученной прямой.
9. Найти угол между прямыми
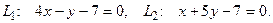 10. От общего уравнения прямой
10. От общего уравнения прямой
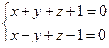 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
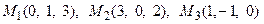 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
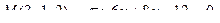 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
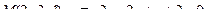 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
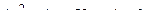 . .
|
|
Вариант 25 | |
1. Вычислить произведение матриц
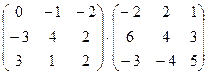 .
2. Вычислить определитель .
2. Вычислить определитель
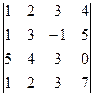 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
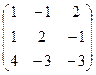 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
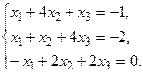 б) Методом Крамера.
б) Методом Крамера.
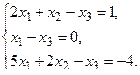 в) Методом Гаусса.
в) Методом Гаусса.
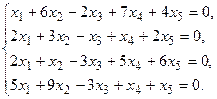 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 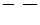 : :
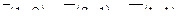
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
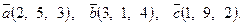 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и 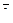 : :
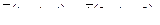 8. Составить уравнение прямой, проходящей через две точки М1(4, 0), М2(2,-4) и найти расстояние от точки Р(-1, -2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(4, 0), М2(2,-4) и найти расстояние от точки Р(-1, -2) до полученной прямой.
9. Найти угол между прямыми
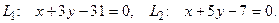 10. От общего уравнения прямой
10. От общего уравнения прямой
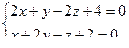 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
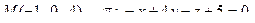 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
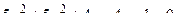 . .
|
|
Вариант 26 | |
1. Вычислить произведение матриц
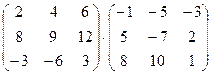 .
2. Вычислить определитель .
2. Вычислить определитель
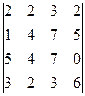 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
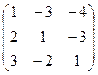 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
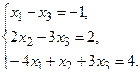 б) Методом Крамера.
б) Методом Крамера.
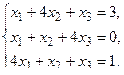 в) Методом Гаусса.
в) Методом Гаусса.
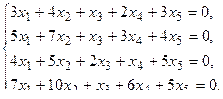 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 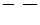 : :
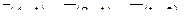
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
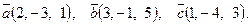 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
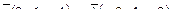 8. Составить уравнение прямой, проходящей через две точки М1(3, 1), М2(0,-1) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3, 1), М2(0,-1) и найти расстояние от точки Р(3,-2) до полученной прямой.
9. Найти угол между прямыми
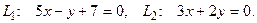 10. От общего уравнения прямой
10. От общего уравнения прямой
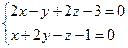 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
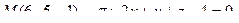 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
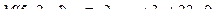 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
|
Вариант 27 | |
1. Вычислить произведение матриц
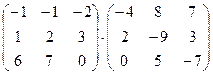 .
2. Вычислить определитель .
2. Вычислить определитель
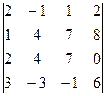 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
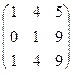 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
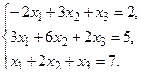 б) Методом Крамера.
б) Методом Крамера.
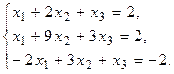 в) Методом Гаусса.
в) Методом Гаусса.
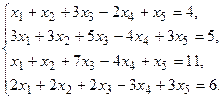 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 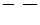 : :
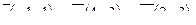
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
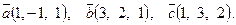 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
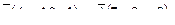 8. Составить уравнение прямой, проходящей через две точки М1(5,-1), М2(2,-2) и найти расстояние от точки Р(5,-5) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(5,-1), М2(2,-2) и найти расстояние от точки Р(5,-5) до полученной прямой.
9. Найти угол между прямыми
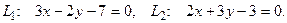 10. От общего уравнения прямой
10. От общего уравнения прямой
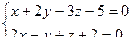 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
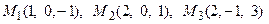 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
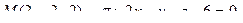 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
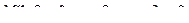 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
|
Вариант 28 | |
1. Вычислить произведение матриц
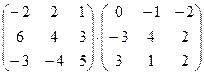 .
2. Вычислить определитель .
2. Вычислить определитель
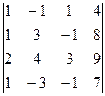 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
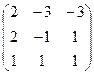 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
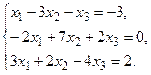 б) Методом Крамера.
б) Методом Крамера.
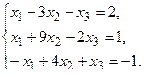 в) Методом Гаусса.
в) Методом Гаусса.
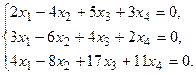 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 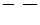 : :
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
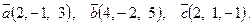 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
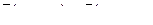 8. Составить уравнение прямой, проходящей через две точки М1(0,-1), М2(2, 4) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(0,-1), М2(2, 4) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
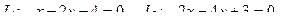 10. От общего уравнения прямой
10. От общего уравнения прямой
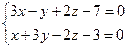 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
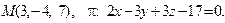 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
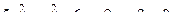 . .
|
|
Вариант 29 | |
1. Вычислить произведение матриц
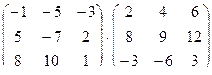 .
2. Вычислить определитель .
2. Вычислить определитель
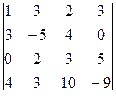 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
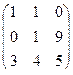 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
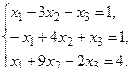 б) Методом Крамера.
б) Методом Крамера.
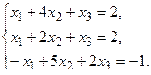 в) Методом Гаусса.
в) Методом Гаусса.
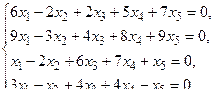 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 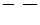 : :
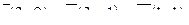
| 6. Установить, являются ли векторы  линейно-зависимыми: линейно-зависимыми:
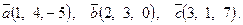 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
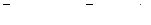 8. Составить уравнение прямой, проходящей через две точки М1(4, 6), М2(3, 4) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(4, 6), М2(3, 4) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
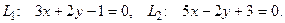 10. От общего уравнения прямой
10. От общего уравнения прямой
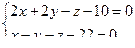 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
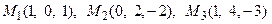 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
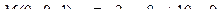 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
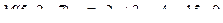 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
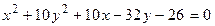 . .
|
|
Вариант 30 | |
1. Вычислить произведение матриц
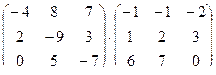 .
2. Вычислить определитель .
2. Вычислить определитель
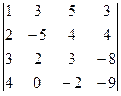 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
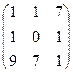 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
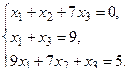 б) Методом Крамера.
б) Методом Крамера.
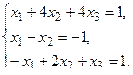 в) Методом Гаусса.
в) Методом Гаусса.
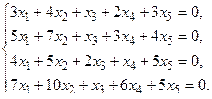 5. Написать разложение вектора
5. Написать разложение вектора 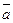 по базису по базису 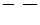 : :
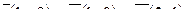
| 6. Установить, являются ли векторы 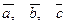 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
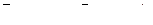 8. Составить уравнение прямой, проходящей через две точки М1(-7, 0), М2(1, 1) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(-7, 0), М2(1, 1) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
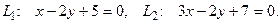 10. От общего уравнения прямой
10. От общего уравнения прямой
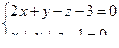 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
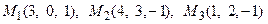 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
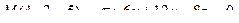 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
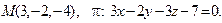 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
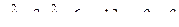 . .
|
Рекомендуемая литература
1. Ашманов И.Л. Введение в математическую экономику. – М.: Наука, 1984.
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1983.
3. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии и линейной алгебре. М., 1987 г.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986.
5. Ефимов Н.В. Квадратичные формы и матрицы. – М.: Наука, 1972.
6. Ефимов Н.В.Аналитическая геометрия. – М.: Наука, 1975.
7. Солодовников А.С., Бабайцев В.А. и др. Математика в экономике: Учебник: В 2-х ч. – М.: Финансы и статистика, 2003.
Дата: 2019-04-23, просмотров: 330.