1. Суммой двух векторов 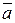 и
и 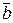 называется вектор
называется вектор 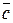 =
= 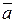 +
+ 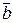 , получаемый по правилам:
, получаемый по правилам:
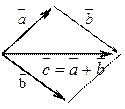 |
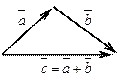 а) правило треугольника; б) правило параллелограмма.
а) правило треугольника; б) правило параллелограмма.
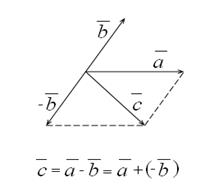
Разностью векторов 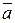 и
и 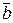 называется вектор
называется вектор 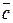 , если
, если 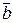 +
+ 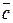 =
= 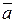 , разность векторов обозначается
, разность векторов обозначается 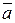 -
- 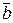 .
.
2. Произведением вектора 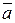 на число l называется вектор l
на число l называется вектор l 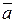 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) |l 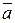 |=|l||
|=|l|| 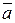 | - модуль вектора l
| - модуль вектора l 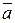 равен произведению модуля вектора
равен произведению модуля вектора 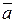 на модуль числа l;
на модуль числа l;
2) l 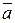
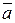 - векторы сонаправлены, если l>0,
- векторы сонаправлены, если l>0,
l 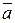 ¯
¯ 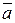 - векторы противоположно направлены, если l<0.
- векторы противоположно направлены, если l<0.
Два вектора 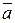 и
и 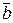 коллинеарны тогда и только тогда, когда выполнено условие:
коллинеарны тогда и только тогда, когда выполнено условие:
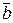 =l
=l 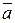 .
.
Проекция вектора на ось
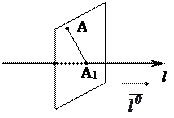 |
Углом между векторами
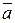 и
и 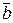 называется наименьший из двух углов j (0 £j£p), на который надо повернуть один вектор, чтобы его направление совпало со вторым после приведения этих векторов к общему началу:
называется наименьший из двух углов j (0 £j£p), на который надо повернуть один вектор, чтобы его направление совпало со вторым после приведения этих векторов к общему началу:
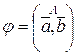 .
.
Рассмотрим ось l, положительное направление которой задано единичным вектором 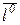 (ортом оси).
(ортом оси).
Проекцией точки А на ось l называется точка пересечения оси l с плоскостью, проходящей через точку А перпендикулярно оси l - точка А1.
Рассмотрим произвольный вектор 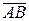 . Пусть точка А1 – проекция начала вектора на ось, В1 - проекция конца вектора.
. Пусть точка А1 – проекция начала вектора на ось, В1 - проекция конца вектора.
Проекцией вектора 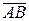 на ось l называется положительное число, равное модулю вектора проекции
на ось l называется положительное число, равное модулю вектора проекции 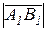 , если угол j между вектором
, если угол j между вектором 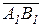 и
и
 |
осью
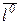 острый, и отрицательное число -
острый, и отрицательное число - 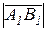 , если угол между вектором
, если угол между вектором 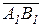 и осью
и осью 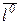 - тупой.
- тупой.
Обозначается проекция вектора 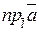 и вычисляется по формуле:
и вычисляется по формуле: 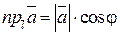 .
.
Линейная зависимость векторов
Выражение 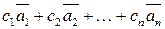 называется линейной комбинацией векторов
называется линейной комбинацией векторов 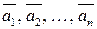 с коэффициентами с1, с2, ..., с n.
с коэффициентами с1, с2, ..., с n.
Система векторов 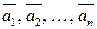 называются линейно зависимой, если их линейная комбинация обращается в ноль
называются линейно зависимой, если их линейная комбинация обращается в ноль 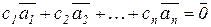 при с1, с2, ..., с n, не равных нулю одновременно; и линейно независимой, если
при с1, с2, ..., с n, не равных нулю одновременно; и линейно независимой, если 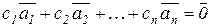 только тогда, когда все коэффициенты с1=с2=...=с n =0.
только тогда, когда все коэффициенты с1=с2=...=с n =0.
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Любые два неколлинеарных вектора линейно независимы. Любая система из трех векторов на плоскости линейно зависима.
Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Любые три некомпланарных вектора линейно независимы. Любая система из четырех векторов в пространстве линейно зависима.
Базис. Координаты вектора
Пусть V – векторное пространство. Базисом в пространстве V называется всякая система векторов 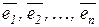 , которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов).
, которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов).
Обозначим через V 1 – множество векторов на прямой; V 2 – множество векторов на плоскости; V 3 - множество векторов в пространстве.
Базисом в V 1 называется любой ненулевой вектор; в V 2 – любая пара неколлинеарных векторов; в V 3 – любая упорядоченная тройка некомпланарных векторов.
Теорема о разложении вектора по базису: Любой вектор можно разложить по базису единственным образом:
1) в V 1: 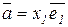 ;
;
2) в V 2: 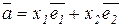 ;
;
3) в V 3: 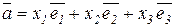 .
.
2.6. Прямоугольная (декартова) система координат
Системой прямоугольных (декартовых координат) называется совокупность точки O и базиса, обозначаемого 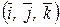 и удовлетворяющего условиям:
и удовлетворяющего условиям:
1) 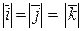 =1;
=1;
2) 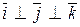 ,
,
3) тройка векторов 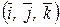 - правая.
- правая.
Любой вектор 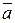 можно представить в виде разложения по базису
можно представить в виде разложения по базису
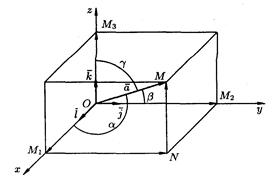 |
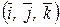 :
:
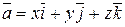 ,
,
числа х, у, z называются прямоугольными (декартовыми) координатами вектора 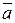 .
.
Геометрический смысл координат вектора – координаты вектора есть проекции этого вектора на координатные оси:
х= 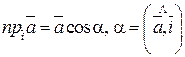 ;
;
у= 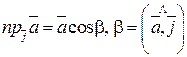 ;
;
z = 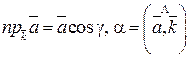 .
.
Cosa , cosb , cosg - называются направляющими косинусами вектора.
Пусть даны точка М1(х1,у1, z 1) и точка М2(х2,у2, z 2), тогда вектор 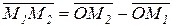 .
.
Координаты вектора 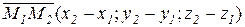 .
.
Модуль вектора 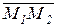 , равный расстоянию между точками М1 и М2, находится по формуле:
, равный расстоянию между точками М1 и М2, находится по формуле:
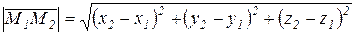 .
.
Рассмотрим векторы 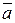 (ха; уа; z а) и
(ха; уа; z а) и 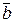 (хb; уb; z b), тогда
(хb; уb; z b), тогда
- если 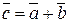 , то
, то 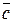 (ха+хb; уа+уb; z а + z b);
(ха+хb; уа+уb; z а + z b);
- если 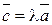 , то
, то 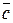 (lха; lуа; lz а).
(lха; lуа; lz а).
Условие коллинеарности векторов в координатной форме:
векторы 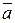 и
и 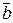 коллинеарны (
коллинеарны ( 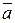 =l
=l 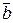 ) тогда и только тогда, когда
) тогда и только тогда, когда
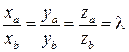 .
.
Координаты середины отрезка М1М2:
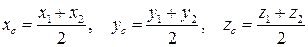 .
.
2.7. Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:
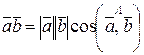 .
.
Алгебраические свойства скалярного произведения:
1) 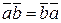 - свойство коммутативности;
- свойство коммутативности;
2) 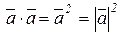 - скалярное произведение вектора на себя равно квадрату модуля вектора;
- скалярное произведение вектора на себя равно квадрату модуля вектора;
3) (a 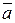 )=a(
)=a( 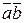 ) – свойство ассоциативности;
) – свойство ассоциативности;
4) ( 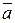 +
+ 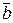 )
) 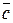 =
= 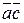 +
+ 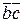 - свойство дистрибутивности.
- свойство дистрибутивности.
Геометрические свойства скалярного произведения:
1) 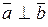 тогда и только тогда, когда
тогда и только тогда, когда 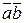 =0 – условие ортогональности векторов;
=0 – условие ортогональности векторов;
2) Два ненулевых вектора 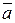 и
и 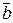 составляют:
составляют:
- острый угол, если 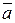
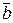 >0;
>0;
- тупой угол, если 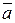
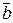 <0;
<0;
Скалярное произведение в координатах двух векторов 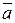 (ха;уа;z а) и
(ха;уа;z а) и 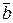 (хb;уb;z b) есть число, равное сумме произведений одноименных координат:
(хb;уb;z b) есть число, равное сумме произведений одноименных координат:
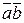 =xaxb + yayb + zazb.
=xaxb + yayb + zazb.
Из определения скалярного произведения вытекают следующие формулы:
- косинус угла между векторами 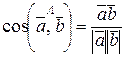 ;
;
- проекция вектора 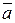 на вектор
на вектор 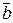 равна
равна 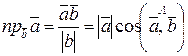 .
.
Дата: 2019-04-23, просмотров: 328.