а) Метод окаймляющих миноров.
Суть метода:
1) берут не равный нулю минор небольшого, обычно 2-го порядка и рассматривают все миноры 3-го порядка, которые содержат (окаймляют) данный. Если все они равны нулю, то ранг матрицы равен 2;
2) если хотя бы один из миноров 3-го порядка не равен нулю, то берут те миноры 4-го – порядка, которые содержат данный ненулевой и вычисляют их. Если все они равны нулю, то ранг матрицы равен 3;
3) если хотя бы один из миноров 4-го порядка не равен нулю, то продолжают процесс.
б) Метод элементарных преобразований.
При элементарных преобразованиях ранг матрицы не изменяется.
Суть метода: элементарными преобразованиями обнуляют как можно большее число элементов матрицы, тогда вычисление ранга не вызывает затруднений.
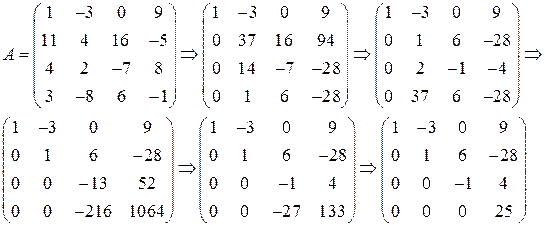 |
Пример.
1) Умножим первую строку матрицы на (-11) и прибавим ко второй; умножим первую строку на (-4) и прибавим к третьей; умножим первую строку на (-3) и прибавим к четвертой.
2) Поменяем местами вторую и четвертую строки матрицы.
3) Умножим вторую строку матрицы на (-2) и прибавим к третьей; умножим вторую строку на (-37) и прибавим к четвертой.
4) Разделим третью строку на 13; разделим четвертую строку на 8.
5) Умножим третью строку матрицы на (-27) и прибавим к четвертой, получим треугольную матрицу, определитель которой не равен нулю.
Rang (А)=4.
Системы линейных уравнений
Определение системы
 |
Пусть дана система m линейных уравнений с n неизвестными.
В матричной форме записи: AX=B, где А-матрица коэффициентов, Х – столбец неизвестных, В – столбец свободных членов.
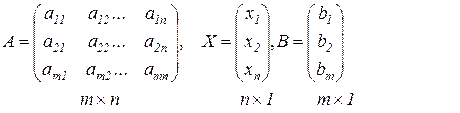 |
Решением системы линейных уравнений называется всякий столбец
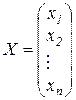
,
удовлетворяющий матричному уравнению АХ=В.
Классификация систем
1) АХ=О (В=О) - однородная система.
2) АХ=В (В¹О) - неоднородная система.
Крамеровские системы
Неоднородная система линейных уравнений называется крамеровской, если выполнены следующие условия:
1) m = n , т.е. число уравнений равно числу неизвестных;
2) detА¹0 – определитель матрицы коэффициентов не равен нулю.
Иначе: система линейных уравнений крамеровская, если А – квадратная невырожденная матрица.
Т.к. А – квадратная матрица, то существует обратная матрица А-1, тогда решение системы дается формулой:
Х=А-1В.
Правило Крамера в матричной форме записи:
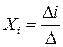
Здесь D равен определителю матрицы коэффициентов, DI есть определитель матрицы коэффициентов, в котором на месте i-го столбца стоит столбец свободных членов.
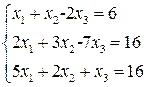 |
Пример. Решить систему уравнений:
1) Вычисляем detА = D и определители Di:
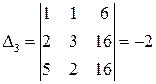 | 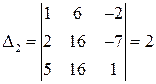 |
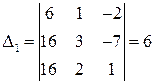
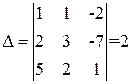
x1= 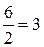 ; x2=
; x2= 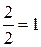 ; x3=
; x3= 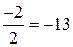 .
.
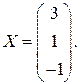 Ответ: решение системы
Ответ: решение системы
1.6.4. Произвольные неоднородные системы
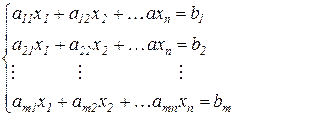 |
Пусть дана система m линейных уравнений с n неизвестными.
Система называется совместной, если у нее существует хотя бы одно решение.
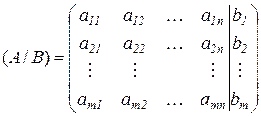 Главную роль в определении совместности системы играет ранг матрицы. Составим матрицу (А/В), которая называется расширенной матрицей.
Главную роль в определении совместности системы играет ранг матрицы. Составим матрицу (А/В), которая называется расширенной матрицей.
Теорема Кронекера – Капелли. Для того чтобы система линейных уравнений была совместна (т.е. имела решение), необходимо и достаточно, чтобы rangA=rang (A/B).
Теорема о числе решений неоднородной системы: пусть для системы из m уравнений с n неизвестными выполнено условие совместности, т.е. r(A)= r(A/B)= r.
Тогда: если r =n , то система имеет единственное решение.
Если r < n , то система имеет бесконечное множество решений.
При этом (n - r) - неизвестным придают произвольное значение, они называются свободными неизвестными;
r - число базисных неизвестных.
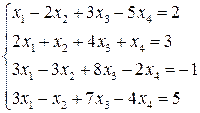 |
Пример. Решить систему линейных уравнений.
Составим расширенную матрицу:
(A/B)= 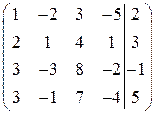
Определим ранги r(A) и r(A/B).
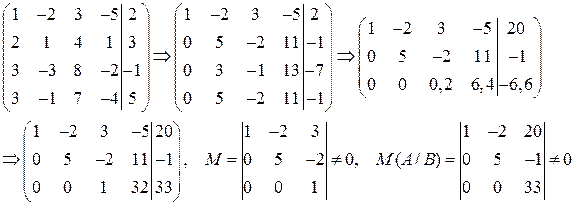
r(A) =r(A/B)=3<4, следовательно, система имеет бесконечное множество решений;
n-r=4-3=1 - одна свободная неизвестная.
r = 3 - три базисных неизвестных.
Т.к. r = 3 , то выберем ненулевой минор третьего порядка, который назовем базисным минором.
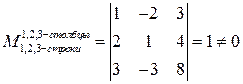
Т.к. в базисный минор входили коэффициенты при х1, х2, х3, то эти неизвестные будут базисными, оставшаяся х4- свободной.
Перепишем систему в виде:
х1-2х2-3х3 =2+5х4
2х1+х2+4х3=3-х4
3х1-3х2+8х3=-1+2х4
Полученная система является крамеровской, т.к. определитель матрицы коэффициентов есть ненулевой минор третьего порядка.
По правилу Крамера выразим х1, х2, х3 через х4.
х1= 30 + 71х4
х2= -7-15х4
х3= -14-32х4
Обозначим х4=С (произвольная константа), тогда общее решение системы имеет вид:

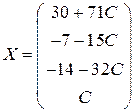
Придавая С различные значения, мы получим бесконечное множество частных решений системы.
Например, 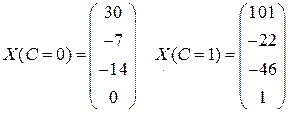 .
.
Однородные системы
Пусть дана однородная система m линейных уравнений с n неизвестными.
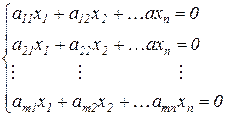
Однородная система всегда совместна, т.к. всегда имеет нулевое (тривиальное) решение Х=0.
Теорема о решении однородной системы. Для того чтобы однородная система с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы r(A)<n.
При m=n условие r(A)<n означает, что определитель матрицы коэффициентов равен нулю.
Пример. Решить систему линейных однородных уравнений.
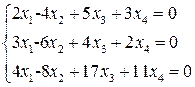
n=4 – число неизвестных.
1) Вычислим r(A) методом окаймляющих миноров.
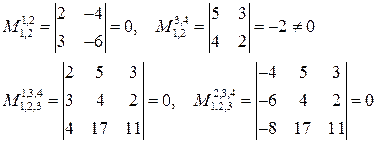
Следовательно, r(A)=2.
2) 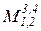 выберем в качестве базисного, тогда система уравнений запишется в виде:
выберем в качестве базисного, тогда система уравнений запишется в виде:
5x3+3x4=-2x1+4x2
4x3+2x4=-3x1+6x2
x1,x2-свободные неизвестные, x3,4-связнные.
Выразим x3,x4 через x1, x2
х3=-2,5x1+5x2
х4=-3,5x1-7x2.
3) Обозначим: x1=С1, x2=С2, тогда общее решение системы:
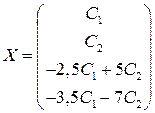
Частные решения:
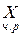 (c1=0,c2=1)=
(c1=0,c2=1)= 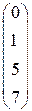
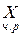 (c1=1,c2=0)=
(c1=1,c2=0)= 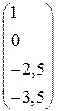
Замечание. Если однородная система имеет хотя бы одно нетривиальное решение, то она имеет бесконечное множество решений.
Общее решение системы есть формула, которая отражает решения системы как функцию свободных неизвестных.
Дата: 2019-04-23, просмотров: 388.