Регулирования

Устойчивость является одним из необходимых условий, обеспе-

чивающих нормальное функционирование автоматических систем.

В линейных САР при отклонении регулируемого параметра от

заданной величины (например, под действием возмущения или из-

менения задания) регулятор воздействует на систему таким образом,

чтобы ликвидировать это отклонение. Если система в результате

этого воздействия возвращается в исходное состояние или переходит

в другое равновесное состояние, то такая система называется устой-

чивой. Если же возникают колебания со все возрастающей амплиту-

дой или происходит монотонное увеличение ошибки регулирования,

то система называется неустойчивой.

Рассмотрим вопросы исследования устойчивости линейной си-

стемы на примере некоторой САР, описываемой линейным диффе-

ренциальным уравнением с постоянными коэффициентами:

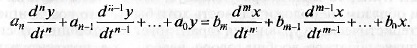
Требуется исследовать устойчивость CAP, иными словами, требу-

ется исследовать устойчивость данного дифференциального уравне-

ния. Самый простой способ — это решить данное уравнение, пред-

ставив решение в виде суммы y(t) = y n (t) +y CB (t), где y( t ) — частное

решение дифференциального уравнения с правой частью, характе-

ризующее установившиеся состояние САР, а усв(0 — общее решение

уравнения с нулевой правой частью, определяющее переходные про-

цессы в САР. Следовательно, устойчивость системы будет опреде-

ляться общим решением усв (t) однородного уравнения

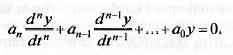
Общее решение этого уравнения можно записать в виде

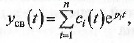
где р i= α,±jβ, — корни характеристического уравнения.

Общее решение y CB (t) будет ограниченным в том случае, если дей-

ствительные части корней характеристического уравнения отрица-

тельны. Таким образом, для устойчивости системы необходимо и

достаточно, чтобы все корни характеристического уравнения

имели отрицательные действительные части.

Если известна передаточная функция линейной САР

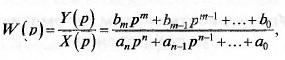
то полином знаменателя совпадает с характеристическим уравнени-

ем однородного дифференциального уравнения. Следовательно, для

устойчивости системы необходимо и достаточно, чтобы все

корни полинома знаменателя (так называемые полюса передаточной

функции) имели отрицательные действительные части.

Для того чтобы определить, устойчива ли данная система, впол-

не достаточно располагать лишь сведениями о знаке действитель-

ных частей этих корней. Существует целый ряд простых критери-

ев, которые по виду характеристического уравнения или знамена-

теля передаточной функции позволяют судить об устойчивости

системы.

Так, положительность всех коэффициентов а, характеристиче-

ского уравнения является необходимым условием устойчивости

системы. Если хотя бы один коэффициент будет отрицательным или

равным нулю, то можно сразу сказать, что система неустойчива.

Таким образом, неположительность хотя бы одного коэффициента

характеристического уравнения гарантирует неустойчивость систе-

мы, однако обратное, вообще говоря, неверно, т.е. положительность

всех коэффициентов уравнения есть необходимое и достаточное

условие лишь для систем первого и второго порядка.

Уже для систем третьего порядка положительность коэффици-

ентов характеристического уравнения недостаточна для устойчи-

вости системы.

Одним из эффективных методов анализа является критерий Гур-

вица, который определяет необходимые и достаточные условия

устойчивости системы любого порядка. Составляется матрица пхп

Гурвица по следующим правилам.

Первая строка заполняется коэффициентами характеристическо-

го уравнения с нечетными индексами, а вторая — коэффициентами

с четными индексами. Дальнейшие строки отличаются от первой

пары смещением вправо на один, два, три и так далее столбца. Все

коэффициенты с индексами, большими п, заменяются нулями. На-

пример, для полинома пятой степени а0+а х р х + а 2 р 2 + а ъ р ъ + а А р Л + a 5 p s

матрица Гурвица имеет вид

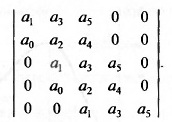
Критерий Гурвица формулируется следующим образом. Все корни

полинома имеют отрицательные вещественные части тогда и только

тогда, когда все п главных миноров матрицы (определителей Гурвица)

положительны. Поскольку для устойчивости полинома необходимо,

чтобы все его коэффициенты были положительными, достаточно

проверить только (n-1) первых определителей Гурвица. Например,

для n = 5 речь идет об определителях

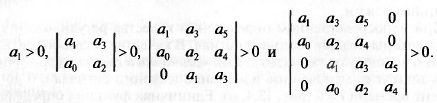
Частотный критерий Найквиста позволяет по амплитудно-

фазовой частотной характеристике (АФЧХ) разомкнутой системы

оценить устойчивость замкнутой системы. АФЧХ может быть полу-

чена экспериментально или аналитически. Аналитическое построение

АФЧХ производится обычными методами.

Для устойчивости замкнутой системы необходимо и достаточно,

чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ж>

не охватывала точку с координатами -1,/0. Если АФЧХ разомкнутой

системы проходит через точку с координатами -1,j0, то система будет

нейтральной.

Критерий Найквиста позволяет наглядно проследить влияние изме-

нения параметров передаточной функции на устойчивость системы.