Любая система, в том числе и САР, состоит из элементов (звеньев).

Для получения модели системы необходимо определить модели ее

элементов. Элементы и сама система характеризуются входом (вхо-

дами) x(t) и выходом (выходами) y(t). Входы независимы, они «при-

ходят» из внешней среды. При изменении информации на входе

меняется внутреннее состояние объекта (так называют его изменяю-

щиеся свойства) и, как следствие, выходы. Построить модель — это

значит найти оператор, связывающий входы и выходы. С его помо-

щью можно предсказать реакцию объекта на любой входной сигнал.

Для упрощения моделей делают следующие допущения: 1) система и

ее элементы обладают свойством стационарности; 2) элементы си-

стемы являются линейными; 3) протекающие процессы являются

непрерывными функциями времени при выполнении нулевых на-

чальных условий.

Математические модели могут быть получены теоретически из

законов физики (законы сохранения массы, энергии, импульса). Эти

модели описывают внутренние связи в объекте и, как правило, наи-

более точны. В общем случае физическая модель линейной системы

описывается дифференциальным уравнением следующего вида:

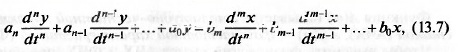
где а„ bj — постоянные коэффициенты, зависящие от параметров

системы.

Применим к левой и правой части преобразование Лапласа, счи-

тая, что все начальные условия нулевые:

Таким образом, передаточная функция равна отношению изо-

бражений по Лапласу выходного и входного сигналов при нулевых

начальных условиях.

Передаточная функция является основной математической моде-

лью, полностью описывающей динамические свойства элемента или

системы. На основе передаточной функции можно получить ряд

частных характеристик системы, исследовать на устойчивость и т.д.

В реальных условиях очень часто на вход системы поступают гар-

монические сигналы. Для определения реакции системы на воздей-

ствие гармонических входных сигналов пользуются амплитудно-

фазовой характеристикой (АФХ), которую получают путем замены в

передаточной функции оператора р на jω

.

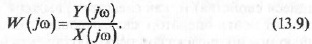АФХ представляет собой комплексное выражение, имеющее со-

ответственно амплитуду и фазу:

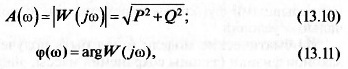
где Р и Q — вещественная и мнимая части АФХ (при условии

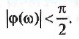
Функция A(iо) называется амплитудно-частотной характери-

стикой (АЧХ), а φ(ω) — фазочастотной характеристикой (ФЧХ).

Чтобы выяснить физический смысл АЧХ и ФЧХ, преобразуем

выражение для АФХ в показательную форму:

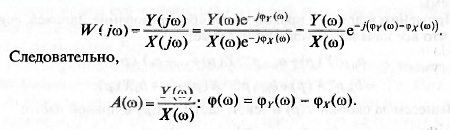
Таким образом, АЧХ — это отношение амплитуд выходного сиг-

нала к входному в зависимости от частоты, а ФЧХ — разность фаз

выходного и входного сигналов в зависимости от частоты.

В качестве примера рассмотрим моделирование звена в виде элек-

трической ЛС-цепи (рис. 13.2).

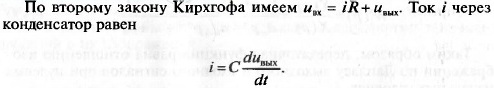
Следовательно, дифференциальное уравнение этого звена запи-

шется в виде

Многие звенья САР независимо от их физической природы описы-

ваются одинаковыми дифференциальными уравнениями, следовательно,

обладают одинаковыми динамическими свойствами. Простейшие звенья

САР, моделируемые дифференциальными уравнениями не выше второ-

го порядка, называются типовыми. Модели типовых звеньев во времен-

ной области и их передаточные функции приведены в приложении 3.

Определение передаточной функции сложной системы, в том

числе САР, производится следующим образом. Структура системы

разбивается на элементы (звенья), передаточные функции которых

либо известны, либо легко определяются. Затем последовательно

объединяют звенья и определяют передаточные функции объединен-

ных звеньев в зависимости от типа их соединения — последователь-

ного, параллельного и с обратной связью.

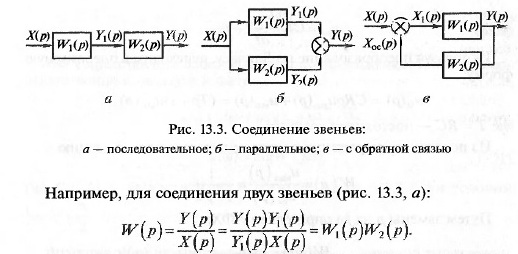
Последовательное соединение звеньев — это соединение, при

котором выходной сигнал предыдущего звена является входным сиг-

налом для последующего. При таком соединении п звеньев переда-

точная функция объединенного звена равна произведению переда-

точных функций исходных звеньев:

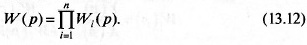
Параллельное соединение звеньев — это соединение, при котором

входной сигнал всех звеньев одинаков, а выходной сигнал представ-

ляет собой сумму выходных сигналов всех звеньев. В этом случае

общая передаточная функция равна сумме передаточных функций

исходных звеньев:

Например, передаточная функция при параллельном соединении

двух звеньев (рис. 13.3, б) равна

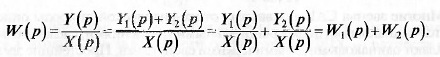
Под обратной связью понимают передачу сигнала с выхода звена

на его вход (рис. 13.3, в). Звено W x (p) называется прямой цепью, а

W 2 (p) — обратной цепью. Различают положительную и отрицатель-

ную обратные связи. Если Х { (р) - Х(р) - Х ос (р), обратная связь от-

рицательная, а при Х х (р) = Х(р) + Х ос (р) — положительная. Для

определения общей передаточной функции запишем передаточные

функции исходных звеньев:

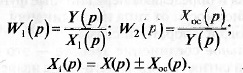
Исключая из этих выражений Х ос (р) к Х х {р), находим передаточную

функцию звена, охваченного обратной связью:

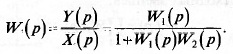
Знак «+» соответствует отрицательной обратной связи, а знак «-» —

положительной. Положительная обратная связь увеличивает коэф-

фициент передачи и уменьшает полосу пропускания прямой цепи, а

отрицательная обратная связь уменьшает коэффициент передачи

прямой цепи и увеличивает полосу пропускания. Кроме того, отри-

цательная обратная связь способствует повышению стабильности

коэффициента передачи прямой цепи.