Как известно, при решении задач математического программирования с ограничениями в форме равенств широко используется метод неопределенных множителей Лагранжа. При определении узловых цен учитываются только активные ограничения, записанные в форме равенств. Больше того, в линейных задачах множители Лагранжа, оказывается, совпадают с двойственными переменными, что позволяет использовать метод Лагранжа для определения узловых цен, в том числе и при учете нелинейностей.
На процесс ценообразования влияют два основных фактора: системные ограничения по режиму работы генерирующих мощностей и по пропускной способности определенных сечений сети и технические потери, связанные с передачей электроэнергии по сети. Что касается технических потерь мощности, то для упрощения задачи примем допущение, что они не зависят от режима и включены в суммарную нагрузку, а режимы линий характеризуются средними потоками мощности.
Для учета системных ограничений в модели (2.7) введем следующие обозначения для неопределенных множителей Лагранжа:
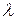 – множитель для баланса мощности;
– множитель для баланса мощности;
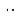 – множитель для выявленного активного ограничения на переток мощности в линии
– множитель для выявленного активного ограничения на переток мощности в линии  ;
;
 – множитель для выявленного активного ограничения на мощность генератора (граничное значение
– множитель для выявленного активного ограничения на мощность генератора (граничное значение 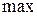 или
или 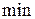 обозначим
обозначим 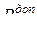 ).
).
Если активные ограничения записать как
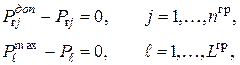
где 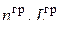 – число генераторов и линий, оказавшихся на граничных (допустимых) значениях, то функция Лагранжа в этом случае может быть записана как
– число генераторов и линий, оказавшихся на граничных (допустимых) значениях, то функция Лагранжа в этом случае может быть записана как
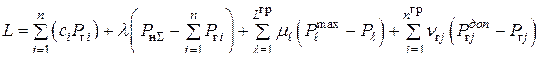 . (2.8)
. (2.8)
Учитывая, что поток в линии может быть записан через коэффициенты токораспределения 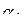 и узловые мощности
и узловые мощности 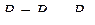 в виде
в виде
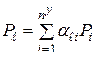 , (2.9)
, (2.9)
в целом 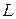 есть функция n генерируемых мощностей
есть функция n генерируемых мощностей 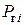 ,
, 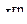 неопределенных множителей
неопределенных множителей 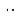 ,
, 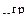 неопределенных множителей
неопределенных множителей 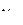 и одного определенного множителя
и одного определенного множителя 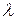 .
.
Дифференцирование функции Лагранжа по переменным, соответствующим мощностям генераторных узлов и неизвестным множителям, дает возможность получить все оптимальные значения мощностей генераторов и множителей Лагранжа путем решения системы:
 . (2.10)
. (2.10)
Формально, множители Лагранжа есть частные производные оптимизируемой целевой функции по правой части соответствующих ограничений.
Первый множитель Лагранжа 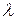 соответствует узловым ценам покрытия нагрузки самым дорогим востребованным генераторным агрегатом при отсутствии режимных ограничений, в этом случае все элементы векторов
соответствует узловым ценам покрытия нагрузки самым дорогим востребованным генераторным агрегатом при отсутствии режимных ограничений, в этом случае все элементы векторов 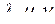 будут равны нулю. Множитель
будут равны нулю. Множитель 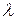 характеризует величину изменения значения целевой функции в результате изменения спроса в определенном узле на 1 МВт.
характеризует величину изменения значения целевой функции в результате изменения спроса в определенном узле на 1 МВт.
Множители Лагранжа к ограничениям по контролируемым связям и внешним перетокам 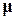 с экономической точки зрения интерпретируются как цены последнего 1 МВт пропускной способности сечений.
с экономической точки зрения интерпретируются как цены последнего 1 МВт пропускной способности сечений.
При наличии ограничений элементы вектора 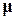 , соответствующие номеру ограничивающей связи, отличны от нуля, поэтому цены в остальных нагрузочных узлах определяются следующим образом:
, соответствующие номеру ограничивающей связи, отличны от нуля, поэтому цены в остальных нагрузочных узлах определяются следующим образом:
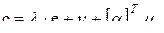 . (2.11)
. (2.11)
Продолжим исследование задачи методом множителей Лагранжа. С учетом найденных активных ограничений по верхней границе Р1, нижней Р3 и потоку по линии, что определяет следующую систему ограничений в форме равенств
Р1 + Р2 + Р3 + Р4 – 500 = 0,
Р1 – 200 = 0,
Р3 – 100 = 0,
Р3 + Р4 – 190 = 0.
Функция Лагранжа примет вид
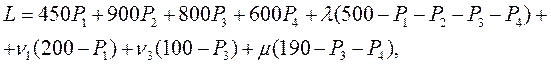
Условие минимума этой функции определяется равенством нулю частных производных по всем неизвестным
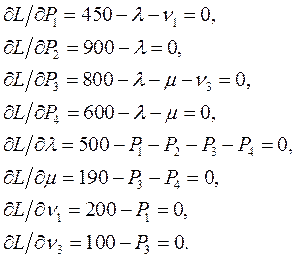
Из первых 4-х уравнений получим следующие значения множителей Лагранжа 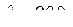
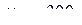
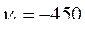 и
и 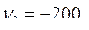
Из остальных уравнений находим мощности генераторов, равные Р1=200, Р2=110, Р3=100 и Р4=90.
В соответствии с формулой (2.11) для узловых цен получим
|
С= | 900 |
+ | -450 |
+ | 0 |
= | 450 |
| 900 | 0 | 0 | 900 | ||||
| 900 | 200 | -300 | 800 | ||||
| 900 | 0 | -300 | 600 |
Дата: 2019-04-23, просмотров: 411.