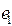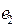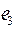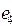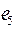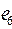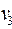1. Из заданного множества А элементарных конъюнкций выделить простые импликанты функции f:
1) A = 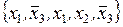 ,
, 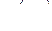 = (00101111);
= (00101111);
2) A =  ,
, 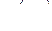 = (01111110);
= (01111110);
3) A =  ,
, 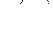 = (1010111001011110);
= (1010111001011110);
4) A = 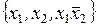 ,
, 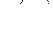 = (1011);
= (1011);
5) A = 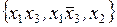 ,
, 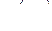 = (00111011);
= (00111011);
6) A = 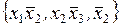 ,
, 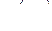 = (00101111).
= (00101111).
2. По заданной ДНФ с помощью метода Блейка построить сокращенную ДНФ:
1) 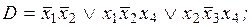
2) 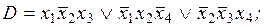
3) 
4) 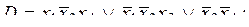
5) 
6) 
7) 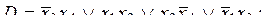
8) 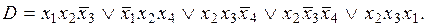
3. Построить сокращенную ДНФ по заданной КНФ:
1) 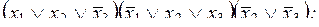
2) 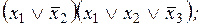
3) 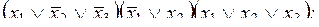
4) 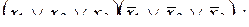
5) 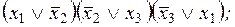
6) 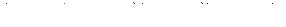
7) 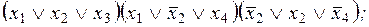
8) 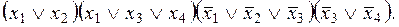
4. Изобразив множество N f функции 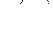 в E n, найти коды максимальных интервалов и постройте сокращенную ДНФ:
в E n, найти коды максимальных интервалов и постройте сокращенную ДНФ:
1)  = (11110100); 2)
= (11110100); 2)  = (01010011);
= (01010011);
3)  = (11010011); 4)
= (11010011); 4)  = (11100111);
= (11100111);
5)  = (1111100001001100); 6)
= (1111100001001100); 6)  = (0001011111101111);
= (0001011111101111);
7)  = (1110011000000111); 8)
= (1110011000000111); 8)  = (1111111111111000).
= (1111111111111000).
5. C помощью алгоритма Квайна построить сокращенную ДНФ для функции f, заданной вектором своих значений:
1)  = (01110110); 2)
= (01110110); 2)  = (10111101);
= (10111101);
3)  = (00101111); 4)
= (00101111); 4)  = (11100100);
= (11100100);
5)  = (0001101111011011); 6)
= (0001101111011011); 6)  = (0000111111110110);
= (0000111111110110);
7)  = (1111111101111110); 8)
= (1111111101111110); 8)  = (0000111101111111).
= (0000111101111111).
6. Найти сокращенную ДНФ функции f с помощью минимизирующей карты:
1)  = (01010111); 2)
= (01010111); 2)  = (11011011);
= (11011011);
3)  = (10110000); 4)
= (10110000); 4)  = (11101111);
= (11101111);
5)  = (0001101111011111); 6)
= (0001101111011111); 6)  = (0011110111111101);
= (0011110111111101);
7)  = (0011110111011110); 8)
= (0011110111011110); 8)  = (0010101111011111).
= (0010101111011111).
7. C помощью минимизирующих карт построить сокращенную ДНФ для частично определенной функции f, заданной векторно (прочерки соответствуют неопределенным значениям):
1)  = (01--01-1); 2)
= (01--01-1); 2)  = (1-01--10);
= (1-01--10);
3)  = (1---0-10); 4)
= (1---0-10); 4)  = (0--10-1-);
= (0--10-1-);
5)  = (10-1-011-0--11); 6)
= (10-1-011-0--11); 6)  = (0--1---0--1-1-01);
= (0--1---0--1-1-01);
7)  = (--01-1-00----1-0); 8)
= (--01-1-00----1-0); 8)  = (-10-1-11-01-0---).
= (-10-1-11-01-0---).
8. Найти длину сокращенной ДНФ функции f:
1) 
2) 
3) 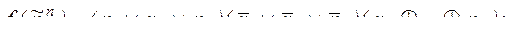
4) 
5) 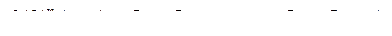
6) 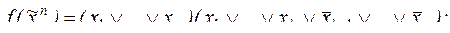
7) 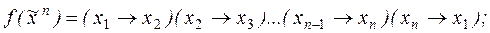
8) 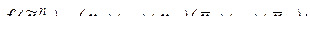
9) 
9. Выяснить, является ли ДНФ D а) тупиковой, б) кратчайшей, в) минимальной:
1) 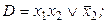
2) 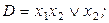
3) 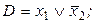
4) 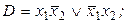
5) 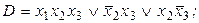
6) 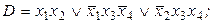
7) 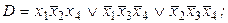
8) 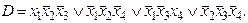
10. Применить алгоритм упрощения к ДНФ:
1) 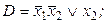
2) 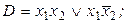
3) 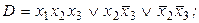
4) 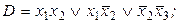
5) 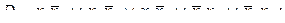
6) 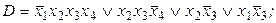
7) 
8) 
11. По заданной сокращенной ДНФ D построить минимальные ДНФ:
1) 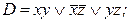
2) 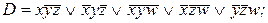
3) 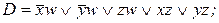
4) 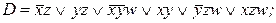
5) 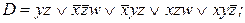
6) 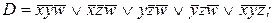
7) 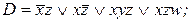
8) 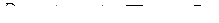
12. C помощью таблицы Квайна построить все тупиковые ДНФ функции f, заданной вектором своих значений:
1)  = (01111100); 2)
= (01111100); 2)  = (01111110);
= (01111110);
3)  = (00011111); 4)
= (00011111); 4)  = (1111100001001100);
= (1111100001001100);
5)  = (1110100001101000); 6)
= (1110100001101000); 6)  = (1110011000010101);
= (1110011000010101);
7)  = (0001011110101110); 8)
= (0001011110101110); 8)  = (0001101111100111).
= (0001101111100111).
ГЛАВА 5. ТЕОРИЯ ГРАФОВ
Основные понятия
Определение. Графом 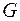 называется любая пара
называется любая пара 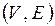 , где
, где 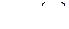 – множество элементов произвольной природы, называемых вершинами графа;
– множество элементов произвольной природы, называемых вершинами графа; 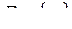 – семейство пар из
– семейство пар из 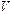 :
: 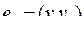 .
.
В множестве 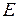 допускаются пары типа
допускаются пары типа 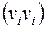 , а также повторяющиеся пары. Если пары
, а также повторяющиеся пары. Если пары  рассматриваются как неупорядоченные, т. е.
рассматриваются как неупорядоченные, т. е. 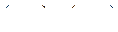 , то граф
, то граф 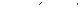 называется неориентированным и пары из множества
называется неориентированным и пары из множества 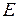 называются ребрами. Если пары считаются упорядоченными, т. е.
называются ребрами. Если пары считаются упорядоченными, т. е. 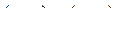 , то граф называется ориентированным или орграфом и эти пары называются ориентированными ребрами или дугами.
, то граф называется ориентированным или орграфом и эти пары называются ориентированными ребрами или дугами.
Пример 1. Рассмотрим граф 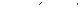 , где
, где  ,
, 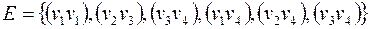 . Условно этот граф можно изобразить следующим образом
. Условно этот граф можно изобразить следующим образом
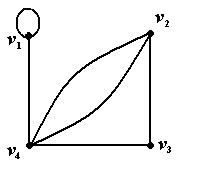
Рис. 5.1
Определение. Ребро вида 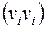 называется петлей при вершине
называется петлей при вершине 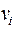 . Повторяющиеся в множестве
. Повторяющиеся в множестве 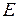 пары называются кратными ребрами.
пары называются кратными ребрами.
Иногда под термином «граф» подразумевается граф без кратных ребер и петель, тогда граф с кратными ребрами называется мультиграфом, а граф с кратными ребрами и петлями – псевдографом. Иногда граф без кратных ребер и петель называют простым графом.
Такое широкое определение графа допускает любую трактовку: множество предприятий с экономическими отношениями, множество людей с психологической совместимостью, система управления с подчинением, технические системы со связями, электрические цепи с источниками и потребителями, транспортные сети. Поэтому язык теории графов получил распространение в химии, физике, лингвистике, экономике, психологии и т. д.
Вершины 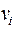 и
и  называются смежными, если либо пара
называются смежными, если либо пара 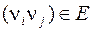 , либо
, либо 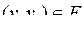 .
.
Вершина 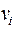 и ребро
и ребро 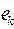 инцидентны, если
инцидентны, если 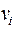 входит в пару
входит в пару 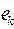 .
.
Ребра 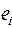 и
и 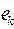 называются смежными, если они инцидентны одной и той же вершине.
называются смежными, если они инцидентны одной и той же вершине.
В неориентированном графе степенью вершины 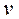
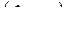 называется количество инцидентных ей ребер, причем петля учитывается дважды. Если
называется количество инцидентных ей ребер, причем петля учитывается дважды. Если  , то вершина
, то вершина 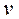 называется изолированной, если
называется изолированной, если  , то вершина
, то вершина 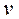 называется висячей.
называется висячей.
Так, в приведенном примере  ,
,  ,
, 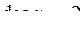 и
и  .
.
Мы будем рассматривать только конечные графы, т. е. множества 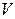 и
и 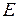 будут конечными, будем обозначать их мощности
будут конечными, будем обозначать их мощности  и
и 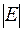 соответственно.
соответственно.
Лемма о рукопожатиях. Если 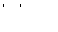 ,
, 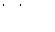 , то
, то 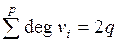 .
.
Доказательство очевидно: каждое ребро в этой сумме участвует ровно 2 раза, так как имеет 2 конца.
Из леммы вытекает, что число вершин с нечетной степенью четно.
Определение. Графы 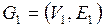 и
и 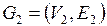 называются изоморфными, если существует биекция
называются изоморфными, если существует биекция 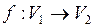 , причем если пара
, причем если пара 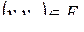 , то пара
, то пара 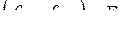 и наоборот.
и наоборот.
Чтобы установить изоморфизм графов, достаточно одинаково занумеровать вершины множества 
 и соответствующие им при биекции
и соответствующие им при биекции 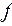 вершины множества
вершины множества 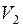 .
.
Пример 2. Графы 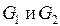 на рис. 5.2 изоморфны.
на рис. 5.2 изоморфны.
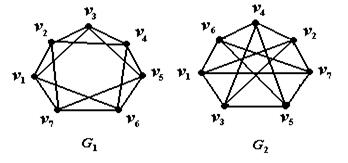
Рис. 5.2
Пример 3. Графы 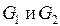 на рис. 5.3 изоморфны.
на рис. 5.3 изоморфны.
Рис. 5.3
Определение. Подграфом в графе 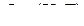 называют граф
называют граф 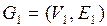 , в котором
, в котором 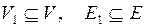 .
.
Графы можно задавать простым рисунком, или перечислением элементов множеств 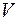 и
и 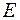 , или матрицами смежности, или матрицей инцидентности.
, или матрицами смежности, или матрицей инцидентности.
Матрица смежности вершин для неориентированного графа – это квадратная матрица размером 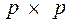 , где
, где 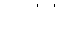 ; элемент матрицы
; элемент матрицы  если пара
если пара 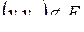 ,
, 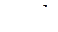 если вершины
если вершины 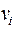 и
и  соединены
соединены  ребрами. Эта матрица позволяет задавать неориентированные графы с кратными ребрами и петлями.
ребрами. Эта матрица позволяет задавать неориентированные графы с кратными ребрами и петлями.
Матрица смежности вершин для графа, приведенного на рис. 5.1, имеет вид
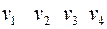
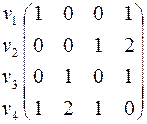 .
.
Aналогично можно задать матрицу смежности ребер для неориентированного графа, в ней элемент  если ребра
если ребра 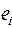 и
и  смежные. Она используется редко.
смежные. Она используется редко.
Матрица инцидентности употребляется часто и позволяет задавать ориентированные графы. Если граф 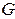 имеет вершины
имеет вершины  и ребра
и ребра  , то матрица инцидентности
, то матрица инцидентности 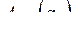 будет иметь размер
будет иметь размер 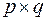 , и
, и 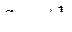 если ребро
если ребро  инцидентно вершине
инцидентно вершине 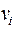 в остальных случаях
в остальных случаях  Если
Если  – петля при вершине
– петля при вершине 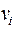 , тогда
, тогда  . Если граф ориентированный, то ориентация ребер указывается стрелкой и
. Если граф ориентированный, то ориентация ребер указывается стрелкой и  если ребро
если ребро  вошло в вершину
вошло в вершину 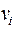 , и
, и  если
если  вышло из вершины
вышло из вершины 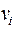 .
.
Обратимся к примеру 1, для того чтобы задать матрицу инцидентности, надо пронумеровать ребра графа. Получим соответствующую матрицу инцидентности.
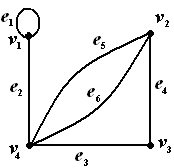 Рис. 5 .4
Рис. 5 .4
|
|
Определение. Простой граф, в котором любые две вершины смежны, называется полным графом и обозначается 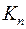 , где n – число вершин.
, где n – число вершин.
Примеры полных графов, представлены на рис. 5.5.
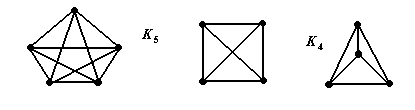 Рис. 5 .5
Рис. 5 .5
|
Если степень каждой вершины графа равна 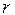 , то граф называется регулярным степени
, то граф называется регулярным степени 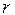 . Графы
. Графы 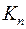 , очевидно, регулярные степени
, очевидно, регулярные степени 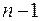 .
.
Допустим, множество вершин графа 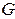 можно разбить на 2 непересекающихся подмножества:
можно разбить на 2 непересекающихся подмножества: 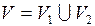 , причем для любого ребра
, причем для любого ребра 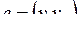 вершины
вершины 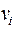 и
и  принадлежат разным подмножествам. Такой граф называется двудольным, примеры двудольных графов приведены на рис. 5.6, рис. 5.7, рис. 5.8
принадлежат разным подмножествам. Такой граф называется двудольным, примеры двудольных графов приведены на рис. 5.6, рис. 5.7, рис. 5.8
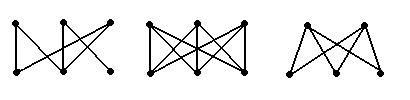 Рис. 5.6 Рис. 5.7 Рис. 5.8
Рис. 5.6 Рис. 5.7 Рис. 5.8
|
Если каждая вершина из 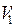 соединена ребром с каждой вершиной из
соединена ребром с каждой вершиной из 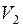 , то такой граф называется полным двудольным графом, обозначается
, то такой граф называется полным двудольным графом, обозначается  , где
, где 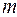 и
и 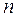 – мощности подмножеств
– мощности подмножеств 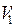 и
и 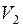 . На рис. 5.7 и рис. 5.8 изображены графы
. На рис. 5.7 и рис. 5.8 изображены графы  и
и  . Cреди полных двудольных графов выделяется граф
. Cреди полных двудольных графов выделяется граф  , который называется звездным графом.
, который называется звездным графом.
Путь, цепь, связность
Определение. Путем в неориентированном графе 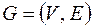 называется любая последовательность вида:
называется любая последовательность вида: 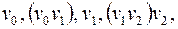
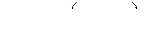 , которая обозначается
, которая обозначается  , все
, все 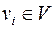 и пары
и пары 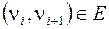 .
.
Путь, где не повторяются ребра, называется цепью. Путь, где не повторяются вершины, называется простой цепью. Длиной пути называется число ребер, входящих в путь.
Путь замкнут, если 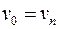 . Замкнутая цепь называется циклом, замкнутая простая цепь – простым циклом.
. Замкнутая цепь называется циклом, замкнутая простая цепь – простым циклом.
Лемма о существовании простой цепи. Пусть 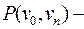 путь из
путь из 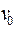 в
в 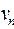 в неориентированном графе
в неориентированном графе 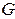 . Тогда можно выбрать подпуть
. Тогда можно выбрать подпуть 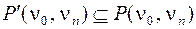 , который будет простой цепью.
, который будет простой цепью.
Доказательство. Если в  вершины не повторяются, то он и есть простая цепь. Если в этом пути существует повторяющаяся вершина
вершины не повторяются, то он и есть простая цепь. Если в этом пути существует повторяющаяся вершина 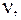 то он имеет вид
то он имеет вид  , где
, где 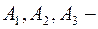 последовательности вершин и ребер.
последовательности вершин и ребер.
Рассмотрим подпуть 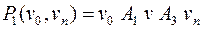 , вершина
, вершина 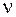 в этом пути уже не повторяется. Если в
в этом пути уже не повторяется. Если в 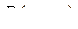 нет повторяющихся вершин, то он и есть простая цепь, и теорема доказана. В противном случае повторим процедуру удаления повторяющейся вершины, так как число ребер и вершин конечно, то процесс завершится и мы получим
нет повторяющихся вершин, то он и есть простая цепь, и теорема доказана. В противном случае повторим процедуру удаления повторяющейся вершины, так как число ребер и вершин конечно, то процесс завершится и мы получим 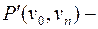 простую цепь.
простую цепь.
Говорят, вершина 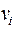 связана с вершиной
связана с вершиной  в неориентированном графе, если существует путь
в неориентированном графе, если существует путь 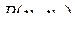 .
.
Определение. Неориентированный граф называется связным, если любые две его вершины связаны.
Cвязанность вершин задает некоторое отношение 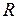 на множестве вершин. Пара
на множестве вершин. Пара  тогда и только тогда, когда существует
тогда и только тогда, когда существует 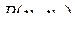 . Будем считать, что
. Будем считать, что 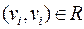 (длина пути в этом случае равна 0). Если
(длина пути в этом случае равна 0). Если 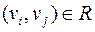 , то
, то 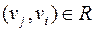 . Если
. Если 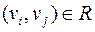 и
и 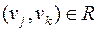 , тогда, очевидно
, тогда, очевидно 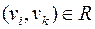 , таким образом, отношение
, таким образом, отношение 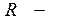 рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Отношение эквивалентности позволяет разбить множество вершин 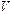 на классы эквивалентности:
на классы эквивалентности:
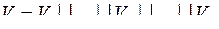 , где
, где 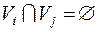 .
.
Две вершины 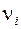 и
и 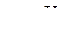 связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
Определение. Cвязной компонентой графа 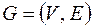 называется подграф
называется подграф  , где
, где  класс эквивалентности на множестве вершин,
класс эквивалентности на множестве вершин, 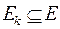 , причем в
, причем в 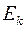 входят все ребра из Е, инцидентные вершинам множества
входят все ребра из Е, инцидентные вершинам множества 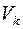 .
.
Каждый неориентированный граф единственным образом представляется в виде объединения своих связных компонент.
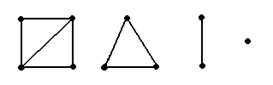 Рис. 5 .9
Рис. 5 .9
|
На рис. 5.9 граф состоит из четырех связных компонент.
Теорема о связи вершин с нечетными степенями. Пусть в неориентированном графе 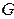 есть ровно 2 вершины с нечетными степенями, тогда они связаны.
есть ровно 2 вершины с нечетными степенями, тогда они связаны.
Доказательство. Пусть 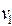 и
и 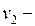 вершины с нечетными степенями. Если они принадлежат одной связной компоненте, то они связаны. Если они принадлежат разным связным компонентам, т. е.
вершины с нечетными степенями. Если они принадлежат одной связной компоненте, то они связаны. Если они принадлежат разным связным компонентам, т. е. 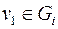 ,
, 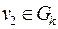 , то в графе
, то в графе 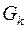 , например, всего одна вершина с нечетной степенью, чего не может быть.
, например, всего одна вершина с нечетной степенью, чего не может быть.
Лемма о присоединении ребра. Если 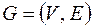 – связный граф,
– связный граф, 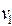 и
и 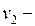 две разные его вершины и
две разные его вершины и 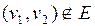 , тогда добавление к графу ребра
, тогда добавление к графу ребра 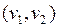 приводит к образованию простого цикла.
приводит к образованию простого цикла.
Доказательство. 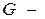 связный граф, поэтому существует путь
связный граф, поэтому существует путь  , в нем можно выделить подпуть
, в нем можно выделить подпуть  , который будет простой цепью.
, который будет простой цепью.
Путь  , который мы получим, идя из
, который мы получим, идя из 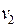 в
в 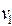 по вершинам и ребрам пути
по вершинам и ребрам пути 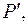 также будет простой цепью. Рассмотрим путь:
также будет простой цепью. Рассмотрим путь: 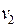

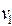
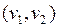
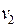 , он будет простым циклом.
, он будет простым циклом.
Лемма об удалении ребра. Пусть 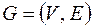 – связный граф, ребро
– связный граф, ребро 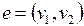 входит в цикл
входит в цикл 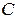 , тогда граф
, тогда граф 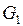 , полученный из
, полученный из 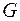 удалением ребра
удалением ребра 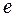 , будет связным.
, будет связным.
Доказательство. Пусть 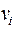 и
и 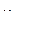 произвольные вершины графа. Так как граф
произвольные вершины графа. Так как граф 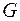 связный, то существует путь
связный, то существует путь  . Если этот путь не содержит ребро
. Если этот путь не содержит ребро  , то
, то 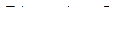 , т.е эти вершины связаны путем и в графе
, т.е эти вершины связаны путем и в графе 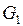 . Если
. Если 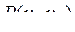 проходит по ребру
проходит по ребру 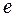 , тогда он имеет вид
, тогда он имеет вид 
 , где
, где 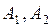 – последовательности ребер и вершин. Ребро
– последовательности ребер и вершин. Ребро  входит в цикл
входит в цикл 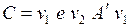 , следовательно, существует цепь
, следовательно, существует цепь 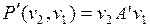 , тогда существует
, тогда существует 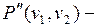 противоположная цепь. Рассмотрим в этом случае путь
противоположная цепь. Рассмотрим в этом случае путь 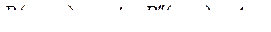 , который не содержит ребро
, который не содержит ребро 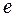 и связывает вершины
и связывает вершины 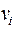 и в
и в  в графе
в графе 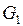 , следовательно,
, следовательно, 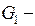 связный граф.
связный граф.
Лемма о числе связных компонент. Пусть 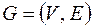 – простой граф, пусть
– простой граф, пусть  – число вершин,
– число вершин, 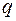 – число ребер,
– число ребер, 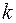 – количество связных компонент. Тогда
– количество связных компонент. Тогда  . Причем, если в
. Причем, если в 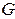 нет циклов, тогда
нет циклов, тогда  .
.
Доказательство. Рассмотрим граф  , в нем
, в нем 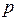 связных компонент. Из графа
связных компонент. Из графа 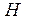 добавлением ребер будем получать граф
добавлением ребер будем получать граф 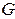 . Добавим первое ребро, число связных компонент уменьшится на 1, добавим еще одно ребро, оно опять свяжет вершины, принадлежащие разным компонентам, и их число уменьшится на 1.
. Добавим первое ребро, число связных компонент уменьшится на 1, добавим еще одно ребро, оно опять свяжет вершины, принадлежащие разным компонентам, и их число уменьшится на 1.
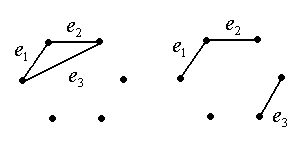
Рис. 5.10 Рис. 5.11
Третье ребро можно добавить, как показано на рис. 5.10, соединяя вершины, принадлежащие одной связной компоненте, в этом случае число связных компонент не уменьшилось. Можно добавить ребро, соединяющее вершины из разных связных компонент, как показано на рис. 5.11, в этом случае число связных компонент вновь уменьшилось на 1.
То есть добавление каждого нового ребра или уменьшает число связных компонент на 1, или оставляет его прежним. Добавление 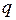 ребер уменьшит число связных компонент максимум на
ребер уменьшит число связных компонент максимум на 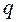 , поэтому
, поэтому  .
.
Если в графе нет циклов, тогда каждое новое добавленное ребро должно соединять вершины из разных связных компонент, поэтому число их каждый раз уменьшается ровно на 1 и  .
.
Теорема о максимальном числе ребер в графе. Пусть 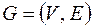 – простой граф (нет петель и кратных ребер), пусть
– простой граф (нет петель и кратных ребер), пусть 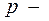 число вершин,
число вершин, 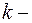 число связных компонент, тогда максимальное число ребер в графе будет
число связных компонент, тогда максимальное число ребер в графе будет
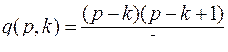 .
.
Замечание. Для связного графа 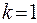 и
и 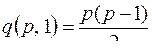 , а это – число ребер в полном графе.
, а это – число ребер в полном графе.
Доказательство. Пусть  -я связная компонента,
-я связная компонента, 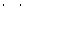 , тогда
, тогда 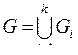 . Так как мы хотим получить максимальное число ребер, пусть все связные компоненты – полные графы, число ребер в
. Так как мы хотим получить максимальное число ребер, пусть все связные компоненты – полные графы, число ребер в 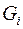 ровно
ровно 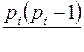 , а общая сумма ребер будет
, а общая сумма ребер будет 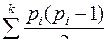 .
.
Наша цель: не меняя общего числа вершин и числа связных компонент, перестроить граф так, чтобы получить максимальное число ребер.
Рассмотрим две связные компоненты 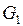 и
и 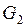 , и пусть
, и пусть 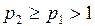 . Построим вместо них полные графы
. Построим вместо них полные графы 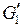 и
и 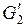 с числом вершин
с числом вершин 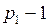 и
и 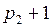 . Общее число вершин не изменилось, посмотрим, как изменилось число ребер:
. Общее число вершин не изменилось, посмотрим, как изменилось число ребер:
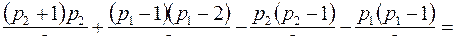
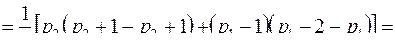
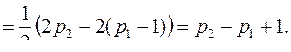
Число ребер увеличилось как минимум на 1.
Проделаем следующую процедуру: выберем связную компоненту с наибольшим числом вершин и будем увеличивать число вершин в этой связной компоненте, за счет уменьшения числа вершин в других связных компонентах, при этом общее число ребер будет все время увеличиваться. Очевидно, оно достигает максимума, когда одна компонента будет полным графом с 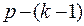 вершинами, а остальные
вершинами, а остальные 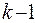 компоненты будут изолированными вершинами и число ребер будет
компоненты будут изолированными вершинами и число ребер будет
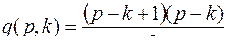 .
.
Следствие. Если 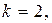 то
то 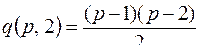 , и это максимальное число ребер при двух связных компонентах. Поэтому если
, и это максимальное число ребер при двух связных компонентах. Поэтому если 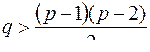 , то граф связный.
, то граф связный.
Дата: 2019-04-23, просмотров: 384.