Например, масса пробы угля для фракционного анализа М = 0,5dmax, кг
где dmax – максимальный размер частиц в пробе, мм.
При обработке результатов фракционного анализа используют формулы:
1. Выход продукта обогащения: 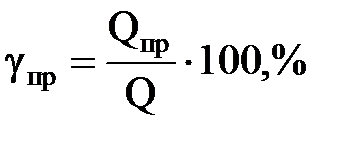
где Qпр и Q – масса полученного продукта и исходного питания, т.
2.Суммарные выходы и среднединамическая зольность:
g = g1 + g2 + … + gn, %;
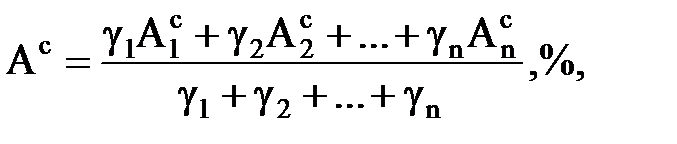
где g, … gn – выход классов, %;
А1с … Аnс – зольность соответствующих классов, %.
3.Категория обогатимости угля определяется в зависимости от выхода приведенных промежуточных фракций плотностью 1,4 – 1,8 г/см3:
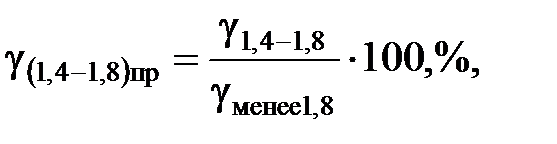
где g1,4-1,8 и gменее1,8 – выход промежуточных фракций 1,4-1,8 г/см3 и суммарный выход фракции меньше 1,8 г/см3 по результатам фракционного анализа, %.
Результаты расчета фракционного анализа угля и его зольность сводим в таблицу
| Плотность фракции,г/см3 |
g, % |
Ас, % | Суммарные, % | |||
| всплывшие фракции | потонувшие фракции | |||||
| сверху g | Ас | снизу g | Ас | |||
| <1,3 | ||||||
| 1,3-1,4 | ||||||
| 1,4-1,5 | ||||||
| 1,5-1,6 | ||||||
| 1,6-1,8 | ||||||
| 1,8> | ||||||
| Итого | ||||||
Далее делаем г рафическ ую интерпретаци ю результатов расчета фракционного анализа :
1. Строим кривую элементарных фракций λ.
На оси ординат откладываем в масштабе суммарные выходы всплывших фракций . Проводим вспомогательные линии, параллельные оси абсцисс, и на этих линиях откладываем в масштабе зольность элементарных фракций . В пределах каждой фракции проводим линии, параллельные оси ординат. Через середины этих линий проводим плавную кривую λ так, чтобы площади заштрихованных криволинейных треугольников были равновелики.
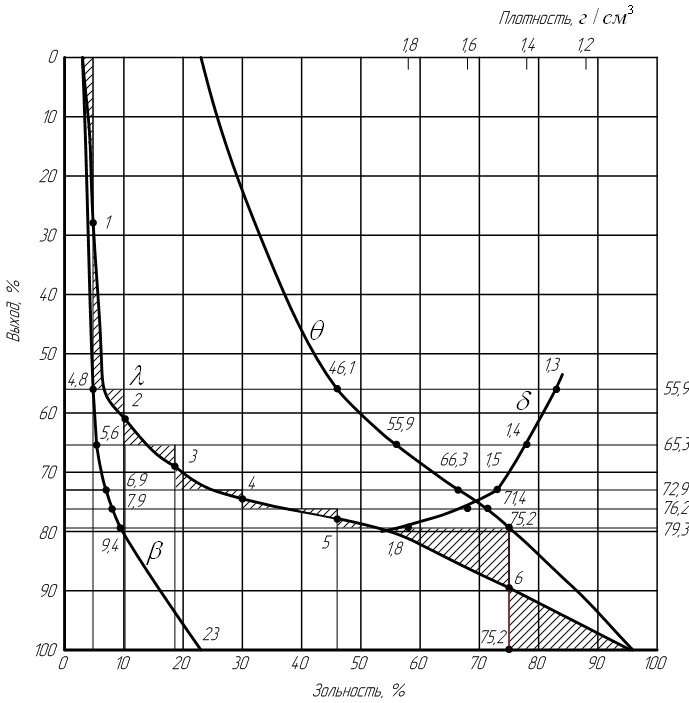
Кривые обогатимости угля класса 13-100 мм
2. Строим кривую всплывших фракций β . На вспомогательных линиях откладываем в масштабе соответствующие значения средней зольности всплывших фракций. Полученные точки соединяем плавной кривой β, начало которой должно совпадать с началом кривой λ.
3. Строим кривую потонувших фракций θ. На вспомогательных линиях откладываем снизу в масштабе значения средней зольности потонувших фракций. Полученные точки соединяем плавной кривой θ, конец которой должен совпадать с концом кривой λ, а начало должно соответствовать концу кривой β на линии, параллельной оси ординат.
4. Строим кривую плотностей δ. На верхней стороне квадрата (принятого за ось плотности) откладываем в масштабе (справа налево) плотность фракций. Через эти точки проводим линии, параллельные оси ординат, до пересечения с соответствующими вспомогательными линиями выходов. Полученные точки соединяем плавной кривой δ.
Дата: 2019-03-05, просмотров: 868.