Распределение скоростей по сечению круглой трубы. Потери напора на трение по длине трубы (формула Пуазейля). Начальный участок потока. Ламинарное движение в плоских и кольцевых зазорах. Особые случаи ламинарного течения (переменная вязкость, облитерация).

Методические указания

В ламинарном потоке частицы жидкости движутся слоями с раз­личными скоростями параллельно оси трубы без перемешивания. В таком потоке касательные напряжения подчиняются закону Ньютона. Используя общий закон распределения касательных напряжений и за­кон Ньютона, можно получить дифференциальное уравнение, из которо­го строго математически выводятся основные закономерности ламинар­ного движения: распределение скоростей по живому сечению трубо­провода; максимальная и средняя скорости; коэффициент Кориолиса α; закон сопротивления трения (формула Пуазейля); коэффициент гид­равлического трения λ в формуле Дарси.

Теоретические результаты хорошо подтверждаются опытом для потоков, в которых отсутствует теплообмен с окружающей средой.

Из формулы Пуазейля следует, что потери напора на трение по длине трубопровода пропорциональны средней скорости потока и коэффициенту кинематической вязкости жидкости.

Литература: [1, с. 75-94]; [2, с. 88-107]; [3, с. 65-74]; [4, с. 94—98]; [5, с. 187—225]; [6, с. 111 — 121]; [8, с. 35—37].

Вопросы для самопроверки

1. Укажите закон распределения касательных напряжений в ци­линдрическом трубопроводе. Для каких режимов этот закон действи­телен? 2. Изобразите эпюру скоростей в цилиндрическом трубопро­воде при ламинарном движении жидкости. Каково соотношение между средней и максимальной скоростями? 3. От каких параметров потока зависят потери на трение по длине при ламинарном движении жид­кости? 4. Каковы особенности движения жидкости в начальном участ­ке ламинарного течения? Как определить длину этого участка и по­тери напора в нем? 5. Каковы особенности движения жидкости в плос­ких и цилиндрических зазорах?

Турбулентное движение жидкости

Особенности турбулентного движения жидкости. Пульсация ско­ростей и давлений. Распределение осредненных скоростей по сечению. Касательные напряжения в турбулентном потоке. Потери напора в трубах. Формула Дарси и коэффициент потерь на трение по длине (коэффициент Дарси). Шероховатость стенок абсолютная и относи­тельная. Графики Никурадзе и Мурина. Гидравлически гладкие и шероховатые трубы. Формулы для определения коэффициента Дарси и область их применения. Турбулентное движение в некруглых трубах.

Методические указания

Турбулентный поток характеризуется беспорядочным, хаотичным движением частиц жидкости. Из-за сложности явлений до сих пор не создано достаточно удовлетворительной теории турбулентного дви­жения, которая непосредственно вытекала бы из основных уравнений гидродинамики и хорошо подтверждалась опытом (как для ламинар­ного движения). Поэтому все выводы и расчетные соотношения полу­чены экспериментально и в результате теоретического исследования упрощенных моделей турбулентного течения.

Прежде всего, следует уяснить механизм турбулентного переме­шивания и пульсации скоростей. Далее рассмотрите структуру и физи­ческую природу касательных напряжений, которые определяются как сумма напряжений, вызванных действием сил вязкости и обусловлен­ных турбулентным перемешиванием. Определение последних основано на полуэмпирических теориях Прандтля и Кармана, получивших даль­нейшее развитие в трудах советских ученых.

Потери на трение по длине определяются по формуле Дарси, ко­торая может быть получена из соображений размерности.

Центральным вопросом темы является определение коэффициента гидравлического трения λ в формуле Дарси. В общем случае коэффи­циент λ является функцией числа Рейнольдса Rе и относительной шеро­ховатости k / d:

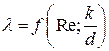                                             ,                                         (3)

где k — абсолютная шероховатость; d — диаметр трубы.

Наиболее полно зависимость (3) раскрывается графиком Нику­радзе, который получен экспериментально на трубах с искусственной зернистой равномерной шероховатостью. На графике можно выделить пять зон, каждая из которых характеризуется определенной внутрен­ней структурой потока и в соответствии с этим определенной зависи­мостью λ от Re и k / d.

1. Зона изменения Rе от 0 до 2320. Ламинарный режим потока. Здесь 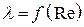. По Пуазейлю,

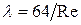                                             .                                                   (4)

2. Зона изменения Rе от 2320 до ~4000. Неустойчивая зона пере­межающейся турбулентности, когда на отдельных участках возникают области турбулентного режима, которые разрастаются, а затем исчезают и снова появляются. Изменение структуры потока сопровождается колебаниями величины λ. Зона не рекомендуется для применения в гидравлических системах.

3. Зона чисел Rе от ~4000 до ~10d / k. Поток характеризуется турбулентным ядром и пристенным (пограничным) ламинарным слоем, который затапливает шероховатости внутренней поверхности трубы, ввиду чего коэффициент λ не зависит от k / d и зависит только от Rе. Здесь трубы работают как «гидравлически гладкие». Для этой зоны, по Блазиусу,

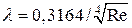                                                                                     (5)

4. Зона, в которой 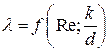. Пределы зоны определяются соотношением 10d / k<Rе<(500d)/ k. Переходная зона к «гидравличе­ски шероховатым» трубам. Пристенный ламинарный слой равен (или меньше) высоте выступов шероховатости.

5. Зона больших чисел Rе>(500d)/ k и, следовательно, интенсив­ной турбулентности. Трубы «гидравлически шероховатые». Коэффици­ент λ не зависит от Rе и является функцией только k / d.

Как показали более поздние исследования, результаты экспери­ментов Никурадзе для «гидравлически шероховатых» труб нельзя пере­нести на трубы с естественной шероховатостью. Оказалось, что в четвертой и пятой зонах общий характер зависимости (3) сохраняет­ся, но вид кривых на графике для различных типов шероховатостей получается различным, т. е. на λ влияет не только величина k / d, но и характер шероховатости стенок труб. Для реальных технических труб с естественной шероховатостью для определения λ в четвертой зоне может быть рекомендована формула Альтшуля

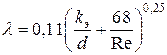                                      ,                                      (6)

а для пятой зоны — формула Шифринсона

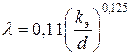                                                                                 (7)

Здесь k _э — эквивалентная абсолютная шероховатость, т. е. такая равно­мерная зернистая шероховатость Никурадзе, которая при расчетах дает такой же коэффициент λ, как и естественная шероховатость.

Отметим, что при малых Rе (<10d / k) формула (6) переходит в формулу (5) для гидравлически гладких труб, а при больших Rе (>500d / k) обращается в формулу (7) для вполне «гидравличе­ски шероховатых» труб.

Вместо расчетных формул (5), (6) и (7) для определения λ можно пользоваться графиком Г. А. Мурина.

Литература: [1, с. 95—106]; [2, с. 108—127]; [3, с. 74—82]; [4, с. 98—111]; [5, с. 226—265]; [6, с. 121 — 130]; [8, с. 37—38].

Вопросы для самопроверки

1. В чем отличие турбулентного течения от ламинарного? 2. Чем отличается распределение скоростей в цилиндрическом трубопроводе при ламинарном и турбулентном режимах движения жидкости? При каком режиме имеет место большая неравномерность скоростей и по­чему? 3. Объясните понятие «гладкие» и «шероховатые» поверхности. Может ли одна и та же труба быть «гидравлически гладкой» и «гид­равлически шероховатой»? В каком случае? 4. Объясните основные линии и зоны сопротивления на графике Никурадзе. 5. Какова зави­симость между потерей напора и средней скоростью течения жидкости в различных зонах и линиях на графике Никурадзе? 6.От каких факторов зависит коэффициент гидравлического трения при турбулент­ном течении и по каким формулам его можно определить? 7. Каковы особенности расчета потерь на трение по длине для некруглых трубо­проводов?