Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Механика жидкости и газа

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ

 

для студентов-заочников

инженерно-технических специальностей

высших учебных заведений

 

 

ИЗДАНИЕ ЧЕТВЁРТОЕ

 

Москва «Высшая школа» 1990

УДК 621.226

Гидравлика: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений /И.А. Гилинский. – 4-е изд.– М.: Высш.шк. ,1990. – 62 с.: ил.
Общие методические указания

 

В первой части курса — гидравлика — изучаются законы равно­весия и движения жидкости, рассматриваются способы применения этих законов к решению практических инженерных задач. Во второй и третьей частях — лопастные гидромашины и гидродинамические передачи, объемные насосы и гидравлические приводы — изучаются устройство и принцип действия, теория и элементы расчета насосов, гидравлических приводов и передач, в которых жидкость служит носи­телем механической энергии.

При изучении материала по учебнику, студент должен особое внимание обратить на проработку основных положений темы (раздела), используя для этой цели методические указания, основное предназна­чение которых — облегчить студенту работу с книгой. Методические указания к каждой теме (разделу) заканчиваются вопросами для самопроверки, охватывающими наиболее существенные положения учебного материала.

Курс целесообразно изучать последовательно по темам (разделам), руководствуясь программой и методическими указаниями. Сначала следует изучить теоретическую часть раздела, затем решить и проана­лизировать приведенные в учебнике и задачниках примеры и задачи с решениями. После этого необходимо ответить на вопросы для самопроверки. Учебный материал можно считать проработанным и усво­енным только при условии, если студент умеет правильно применить теорию для решения практических задач.

Существенное значение имеет правильный выбор учебника. Не следует одновременно пользоваться несколькими учебниками. Один из учебников, рекомендуемый в списке учебной литературы, должен быть принят в качестве основного. Другие учебники и учебные пособия используют в том случае, если прорабатываемый раздел отсутствует или недостаточно подробно изложен в основном учебнике.

                                              ЛИТЕРАТУРА

                                                         Основная

1. Гидравлика, гидравлические машины и гидравлические приводы/Башта Т. М., Руднев С. С., Некрасов Б. Б. и др. М., 1982.

2. Некрасов Б. Б. Гидравлика и ее применение на летательных аппаратах. М., 1967.

3. Гидравлика и гидропривод/Гейер В.Т., Дулин В.С., Боруменский А.Г., Заря А.Н. М., 1970.

4. Осипов П.Е. Гидравлика и гидравлические машины. М., 1965.

5. Сборник задач по машиностроительной гидравлике/Под ред. И.И. Куколевского и Л.Г. Подвидза. М., 1981.

6. Лабораторный курс гидравлики, насосов и гидропередач/Под ред. С.С. Руднева и Л.Г. Подвидза. М., 1974.

Дополнительная

7. Башта Т.М. Машиностроительная гидравлика: Справочное пособие. М., 1971.

8. Ковань П.В. Гидропривод горных машин. М., 1967.

9. Ибатулов К.А. Гидравлические машины и механизмы в нефтянности. М., 1972.

 

                                  МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ТЕМАМ И РАЗДЕЛАМ КУРСА

ЧАСТЬ I. ГИДРАВЛИКА

 

Основные свойства жидкости

Определение жидкости. Силы, действующие на жидкость. Давление в жидкости. Сжимаемость. Закон Ньютона для жидкостного трения. Вязкость. Поверхностное натяжение. Давление насыщенного пара жидкости. Растворение газов в жидкости. Модель идеальной жидкости. Неньютоновские жидкости.

Методические указания

По своим физическим свойствам жидкости занимают промежуточ­ное положение между твердыми телами и газами. Жидкость мало изменяет свой объем при изменении давления или температуры, в этом отношении она сходна с твердым телом. Жидкость обладает текучестью, благодаря чему она не имеет собственной формы и принимает форму того сосуда, в котором находится. В этом отношении жидкость отличается от твердого тела и имеет сходство с газом. Свойства жидкостей и их отличие от твердых тел и газов обуславливаются молекулярным строением. Следует уяснить, каким образом особенности молекулярного строения влияют на физические свойства жидкости.

Покоящаяся жидкость подвержена действию двух категорий внешних сил: массовых и поверхностных. Массовые силы пропорциональны массе жидкости или для однородных жидкостей – ее объему. Внешние поверхностные силы непрерывно распределены по граничной поверх­ности жидкости. Следует знать, какие силы относятся к массовым (объемным) и к поверхностным силам, какие силы называются внеш­ними и какие внутренними.

В покоящейся жидкости может существовать только напряжение
сжатия, т. е. давление. Необходимо чётко представлять разницу между понятиями среднего гидростатического давления, гидростатического давления в точке, выраженных в единицах напряжения, и понятием суммарного гидростатического давления на поверхность, выраженного в единицах силы.

В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (на­пример, плотность). Студенту нужно уметь определять основные физи­ческие характеристики жидкости, знать единицы этих характеристик.

Следует также рассмотреть основные физические свойства капель­ных жидкостей: сжимаемость, тепловое расширение, вязкость и др.

Вязкостью называется свойство жидкости оказывать сопротивление относительному перемещению слоев, вызывающему деформацию сдвига. Это свойство проявляется в том, что в жидкости при ее движении возникает сила сопротивления сдвигу, называемая силой внутреннего трения. При прямолинейном слоистом движении жидкости сила внут­реннего трения Т между перемещающимися один относительно другого слоями с площадью соприкосновения S определяется законом Ньютона:

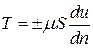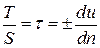                               или .                      (1)                                                           

Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свой­ствами жидкости и ее температурой. Как видно из (1), сила Т и каса­тельное напряжение 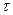 пропорциональны градиенту скорости u и по нор­мали n к поверхности трения 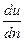, который представляет собой изменение скорости жидкости в направлений нормали на единицу длины нормали. Жидкости, для которых зависимость изменения каса­тельных напряжений от скорости деформации отличается от закона Ньютона (1), называются неньютоновскими или аномальными жид­костями.

Учет сил вязкости значительно осложняет изучение законов дви­жения жидкости. С другой стороны, капельные жидкости незначи­тельно изменяют свой объем при изменении давления и температуры. В целях упрощения постановки задач и их математического решения создана модель идеальной жидкости. Идеальной жидкостью называется воображаемая жидкость, которая характеризуется полным отсутствием вязкости и абсолютной неизменяемостью объема при изменении давления и температуры. Переход от идеальной жидкости к реальной осуществляется введением в конечные расчетные формулы поправок, учитывающих влияние сил вязкости и полученных, главным образом, опытным путем. При изучении гидродинамики следует проследить осо­бенности перехода от идеальной жидкости к реальной.

В гидравлике жидкость рассматривается как сплошная среда (континуум), т.е. среда, масса которой распределена по объему непрерывно. Это позволяет рассматривать все характеристики жид­кости (плотность, вязкость, давление, скорость и др.) как функции координат точки и времени, причем в большинстве случаев эти функции предполагаются непрерывными.

Литература: [1, с. 8—15]; [2, с: 9—18]; [3, с. 9—17]; [14, с. 9—14]; [6, с. 4—12]; [8, с. 5-10].

 

Вопросы для самопроверки

1. В чем отличие жидкостей от твердых тел и газов? 2. Какова взаимосвязь между плотностью и удельным весом жидкости? Укажите их единицы. 3. Что называется коэффициентом объемного сжатия жид­кости? Какова его связь с модулем упругости? 4. Что называется вязкостью жидкости. В чем состоит закон вязкого трения Ньютона? 5. В чем принципиальная разница между силами внутреннего трения в жидкости и силами трения при относительном перемещении твердых тел? 6. Какова связь между динамическим и кинематическим коэффи­циентами вязкости? Укажите их единицы. 7. Укажите свойства идеаль­ной жидкости. С какой целью в гидравлике введено понятие об идеаль­ной жидкости? В каких случаях при практических расчетах жидкость можно считать идеальной?

 

Гидростатика

Свойства давления неподвижной жидкости. Уравнение Эйлера равновесия жидкости. Интегрирование уравнения Эйлера. Поверхности равного давления. Свободная поверхность жидкости. Основное уравнение гидростатики. Закон Паскаля. Приборы для измерения давления. Сила давления жидкости на плоские и криволинейные стенки. Закон Архимеда. Плавание тел. Относительный покой жидкости.

Методические указания

Два свойства гидростатического давления обусловлены тем, что покоящаяся жидкость не воспринимает касательных и усилий. Знание этих свойств позволяет понять форму статического силового воздействия жидкости.

Наиболее общими уравнениями гидростатики являются дифференциальные уравнения Эйлера, устанавливающие и поверхностными силами, действующими в жидкости. При изучении этих уравнений следует усвоить физический смысл всех входящих в них величин. Эти уравнения позволяют просто и быстро решать задачи как в случае абсолютного покоя жидкости, когда на жидкость из массовых сил действует только сила тяжести, так и в случае относительного покоя, когда к силе тяжести присоединяются силы инерции. В случае действия на жидкость одной лишь силы тяжести интегрирование урав­нений Эйлера дает основное уравнение гидростатики

                                                р₂=р₁+ γh ,                                                     (2)

где р₁ и р₂ —давления в точках 1 и 2; h — глубина погружения точки 2 относительно точки 1; 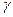— удельный вес жидкости; 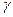h — весо­вое давление столба жидкости глубиной h.

В зависимости от способа отсчета различают абсолютное, избыточ­ное (манометрическое) и вакуумметрическое давление. Следует знать взаимосвязь этих величин.

В уравнении (2) точка 1 может лежать на свободной поверхности жидкости. При этом весовое давление 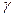h будет избыточным давлением только в том случае, когда давление на свободную поверхность равно атмосферному давлению.

Весьма важными понятиями в гидравлике являются пьезометрическая высота и гидростатический напор. Пьезометрическая высота выражает в метрах столба жидкости избыточное (или абсолютное) давление в рассматриваемой точке жидкости. Гидростатический напор равен сумме геометрической z и пьезометрической р/γ высот. Для всех точек данного объема покоящейся жидкости гидростатический напор относительно выбранной плоскости сравнения есть постоянная величина.

Воздействие жидкости на плоские и криволинейные поверхности наглядно отражается эпюрами давления. Площадь (объем) эпюры дает величину силы давления, а центр тяжести этой площади (объема) — точку приложения силы давления. Аналитическое рассмотрение задачи позволяет получить весьма простые расчетные формулы. В случае плоской поверхности любой формы величина силы гидростатического давления равна смоченной площади этой поверхности, умноженной на гидростатическое давление в центре тяжести площади. Точка приложения силы гидростатического давления (центр давления) лежит всегда ниже центра тяжести (за исключением давления на горизонтальную плоскость, когда они совпадают). Следует указать, что формула для определения координаты центра давления дает точку приложения силы только гидростатического давления без учета давления на свободную поверхность (см. вывод формулы в любом учебнике гидравлики).

 Для криволинейных цилиндрических поверхностей обычно опреде­ляют горизонтальную и вертикальную составляющие полной силы гидростатического давления. Определение вертикальной составляющей связано с понятием «тела давления», которое представляет собой действительный или воображаемый объем жидкости, расположенный над цилиндрической поверхностью. Линия действия горизонтальной составляющей проходит через центр давления вертикальной проекции криволинейной поверхности, а линия действия вертикальной состав­ляющей — через центр тяжести тела давления.

При изучении этого раздела студенту полезно рассмотреть несколь­ко конкретных примеров построения тел давления для цилиндриче­ских поверхностей, определить самостоятельно вертикальную и гори­зонтальную составляющие силы давления, точки их приложения результирующую силу.

Необходимо рассмотреть давление жидкости на стенки труб и резервуаров н расчетные формулы для определения толщины их стенок.

Литература: [1, с. 16—39]; [2, с. 19—47]; [3, с, 17—34]; [4, с. 15—60]; [5, с. 7—103]; [6 с. 12—16]; [8, с. 10—22]

 

Вопросы для самопроверки

1. Каковы свойства гидростатического давления? 2. Объясните физический смысл величин, входящих в дифференциальные уравнения равновесия жидкости Эйлера. 3. Что такое поверхность равного давле­ния и каковы ее форма и уравнение при абсолютном покое жидкости, в случае движения сосуда по горизонтальной плоскости с ускорением, при вращении сосуда вокруг вертикальной оси? 4. Как формулируется закон Паскаля и какова его связь с основным уравнением гидроста­тики? 5. Приведите примеры гидравлических установок, действие кото­рых основано на законе Паскаля. 6. Каковы соотношения между абсо­лютным давлением, избыточным и вакуумом? Что больше: абсолютное давление, равное 0,12 МПа, или избыточное, равное 0,06 МПа? 7. Чему равна пьезометрическая высота (в метрах водяного столба) для атмо­сферного давления? 8. Почему центр давления всегда находится ниже центра тяжести смоченной поверхности наклонной плоской стен­ки? 9. Сформулируйте закон Архимеда. В каких случаях положение судна будет остойчивым и неостойчивым?

Методические указания

Одним из основных уравнений гидродинамики является уравнение постоянства расхода (уравнение неразрывности), которое для плавно изменяющегося и параллельностройного движения может быть пред­ставлено в виде v·S= const (вдоль потока), откуда для двух сечений 1 и 2 получим v₁/v₂= S ₂ / S ₁, т.е. средние скорости потока обратно пропорциональны площадям живых сечений.

Следует уяснить, что уравнение постоянства расхода справедливо только при соблюдении ряда допущений, на которых основан логиче­ский вывод этого уравнения.

Дифференциальные уравнения движения идеальной жидкости Эй­лера дают общую зависимость между скоростями и ускорениями движущихся частиц жидкости и силами, действующими на эти частицы. Интегрирование этих уравнений для элементарной струйки идеальной жидкости приводит к основному уравнению гидродинамики — уравне­нию Бернулли, которое можно получить также и непосредственно, при­менив к бесконечно малому объему жидкости теоремы механики, например теорему живых сил.

Уравнение Бернулли представляет собой частный случай закона сохранения энергии. Все члены уравнения Бернулли отнесены к единице веса жидкости, поэтому все виды энергии в этом уравнении имеют линейную размерность. При рассмотрении уравнения Бернулли для простейшего случая движения элементарной струйки невязкой (идеаль­ной) жидкости следует уяснить геометрический и физический (энер­гетический) смысл уравнения в целом и его отдельных членов, а также обратить внимание на условия применимости уравнения Бернулли к элементарной струйке.

При распространении уравнения Бернулли для элементарной струй­ки на поток реальной жидкости возникает ряд трудностей, которые пре­одолеваются введением соответствующих ограничений и поправок. Уравнение Бернулли составляется для двух живых сечений потока, в которых течение параллельностройное или плавно изменяющееся. Живые сечения здесь плоские, поэтому отсутствуют ускорения вдоль живых сечений, а из массовых сил действует только сила тяжести. Следовательно, в этих сечениях (участках) справедливы законы гид­ростатики, в частности постоянство гидростатического напора для всех точек живого сечения относительно любой плоскости сравнения. Между плавно изменяющимися течениями (участками) потока, связанными уравнением Бернулли, поток может быть и резко изменяющимся. При определении кинетической энергии потока по средней скорости в данном сечении вводится поправка в виде коэффициента Кориолиса α, учи­тывающего неравномерность распределения скоростей по живому се­чению.

При решении практических инженерных задач уравнение Бернулли и уравнение постоянства расхода используются совместно. При этом они составляют систему из двух уравнений, позволяющую решать задачи с двумя неизвестными.

Если для струйки идеальной жидкости уравнение Бернулли пред­ставляет собой закон сохранения механической энергии, то для потока реальной жидкости дно является уравнением баланса энергии с учетом гидравлических потерь. Гидравлическими потерями называется работа сил трения, затраченная на перемещение единицы веса жидкости из одного сечения в другое. Энергия потока, израсходованная на работу сил трения, превращается в тепловую энергию и рассеивается в про­странстве.

Литература: [1, с. 40—61]; [2, с. 48—72]; [3. с. 37—57]; [4, с. 61—87]; [6, с. 16—21]; [8, с. 23—32].

 

Вопросы для самопроверки

1. Дайте определение и приведите примеры основных видов дви­жения жидкости: установившегося и неустановившегося, напорного и безнапорного, равномерного и неравномерного, медленно изменяю­щегося. 2. Что такое линия тока, трубка тока и элементарная струйка? 3. При каких условиях сохраняется постоянство расхода вдоль потока? 4. Укажите физический смысл величин, входящих в дифференциальные уравнения гидродинамики Эйлера. 5. Объясните геометрический и физи­ческий смысл понятий: геодезический, пьезометрический и гидравли­ческий уклоны. Может ли быть отрицательным гидравлический уклон? пьезометрический уклон? 6. Когда линия полной энергии и пьезометри­ческая линия параллельны? Когда в направлении движения жидкости эти линии сближаются и когда удаляются одна от другой? 7. Какие существуют ограничения в применении уравнения Бернулли? 8. К каким выражениям приводится уравнение Бернулли в случаях: а) неподвиж­ной жидкости; б) равномерного движения в горизонтальном трубо­проводе; в) истечения жидкости из сосуда через круглое небольшое отверстие. 9. Каковы причины возникновения потерь напора при движении вязкой жидкости? Дайте определение понятию «гидравличе­ские потери напора».

 

Методические указания

Для использования уравнения Бернулли при решении практических инженерных задач необходимо знать гидравлические потери (потери напора), имеющие место при движении жидкости. Эти потери в зна­чительной степени зависят от того, будет ли режим движения в потоке турбулентным или ламинарным.

Наличие того или иного режима в трубопроводе обусловливается соотношением трех факторов, входящих в формулу безразмерного критерия Рейнольдса 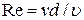, где v — средняя скорость движения жидкости; d — диаметр трубопровода;  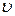— коэффициент кинематиче­ской вязкости.

При изучении режимов движения жидкости следует уяснить раз­личия в структуре потоков. Нужно знать формулу числа Рейнольдса и его критическое значение, отчетливо представлять его физический смысл.

В гидравлике широко применяется метод моделирования, когда исследуется не само явление или установка, а их модель, обычно меньших размеров. Основой моделирования является теория гидродинамического подобия.

Для установившегося движения однородных несжимаемых жидкостей необходимым и достаточным условием гидродинамического подобия является геометрическое, кинематическое и динамическое подобие потоков. Следует четко представлять содержание этих частич­ных критериев подобия. Для полного гидродинамического подобия необходима пропорциональность всех сил, действующих в потоке, но подобие по одним силам часто исключает подобие по другим силам. Поэтому считается достаточным получение приближенного подобия по силам, преобладающим в данном потоке. Критериями такого подобия являются критерий Рейнольдса (преобладание сил трения), критерий Фруда (силы тяжести), критерий Эйлера (силы давления).

Особое внимание следует обратить на критерий Рейнольдса. Он представляет собой отношение сил инерции к силам трения. Теперь можно более глубоко разобраться в физическом смысле числа, или критерия Рейнольдса: режимы движения жидкости и переход одного режима в другой объясняются преобладанием силы инерции или силы трения в потоке, т. е. величиной Rе. Как будет видно из дальнейшего, многие величины, характеризующие движение жидкости, могут быть представлены как функции Rе.

Литература: [1, с. 62—74]; [2, с. 73—87]; [3, с. 57—65]; [4, с. 90—94]; [5, с. 103—120]; [6, с. 21—28]; [8, с. 33—35, 64—67].

 

Вопросы для самопроверки

1. От каких характеристик потока зависит режим движения жид­кости? 2. В чем отличие турбулентного течения от ламинарного? 3. Поясните физический смысл и практическое значение критерия Рейнольдса. 4. Сформулируйте условия гидродинамического подобия потоков и гидравлических машин. 5. Объясните физический смысл критериев Рейнольдса, Фруда, Эйлера. В каких случаях должны применяться эти критерии?

Методические указания

В ламинарном потоке частицы жидкости движутся слоями с раз­личными скоростями параллельно оси трубы без перемешивания. В таком потоке касательные напряжения подчиняются закону Ньютона. Используя общий закон распределения касательных напряжений и за­кон Ньютона, можно получить дифференциальное уравнение, из которо­го строго математически выводятся основные закономерности ламинар­ного движения: распределение скоростей по живому сечению трубо­провода; максимальная и средняя скорости; коэффициент Кориолиса α; закон сопротивления трения (формула Пуазейля); коэффициент гид­равлического трения λ в формуле Дарси.

Теоретические результаты хорошо подтверждаются опытом для потоков, в которых отсутствует теплообмен с окружающей средой.

Из формулы Пуазейля следует, что потери напора на трение по длине трубопровода пропорциональны средней скорости потока и коэффициенту кинематической вязкости жидкости.

Литература: [1, с. 75-94]; [2, с. 88-107]; [3, с. 65-74]; [4, с. 94—98]; [5, с. 187—225]; [6, с. 111 — 121]; [8, с. 35—37].

 

Вопросы для самопроверки

1. Укажите закон распределения касательных напряжений в ци­линдрическом трубопроводе. Для каких режимов этот закон действи­телен? 2. Изобразите эпюру скоростей в цилиндрическом трубопро­воде при ламинарном движении жидкости. Каково соотношение между средней и максимальной скоростями? 3. От каких параметров потока зависят потери на трение по длине при ламинарном движении жид­кости? 4. Каковы особенности движения жидкости в начальном участ­ке ламинарного течения? Как определить длину этого участка и по­тери напора в нем? 5. Каковы особенности движения жидкости в плос­ких и цилиндрических зазорах?

Методические указания

Турбулентный поток характеризуется беспорядочным, хаотичным движением частиц жидкости. Из-за сложности явлений до сих пор не создано достаточно удовлетворительной теории турбулентного дви­жения, которая непосредственно вытекала бы из основных уравнений гидродинамики и хорошо подтверждалась опытом (как для ламинар­ного движения). Поэтому все выводы и расчетные соотношения полу­чены экспериментально и в результате теоретического исследования упрощенных моделей турбулентного течения.

Прежде всего, следует уяснить механизм турбулентного переме­шивания и пульсации скоростей. Далее рассмотрите структуру и физи­ческую природу касательных напряжений, которые определяются как сумма напряжений, вызванных действием сил вязкости и обусловлен­ных турбулентным перемешиванием. Определение последних основано на полуэмпирических теориях Прандтля и Кармана, получивших даль­нейшее развитие в трудах советских ученых.

Потери на трение по длине определяются по формуле Дарси, ко­торая может быть получена из соображений размерности.

Центральным вопросом темы является определение коэффициента гидравлического трения λ в формуле Дарси. В общем случае коэффи­циент λ является функцией числа Рейнольдса Rе и относительной шеро­ховатости k / d:

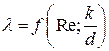                                             ,                                         (3)

где k — абсолютная шероховатость; d — диаметр трубы.

Наиболее полно зависимость (3) раскрывается графиком Нику­радзе, который получен экспериментально на трубах с искусственной зернистой равномерной шероховатостью. На графике можно выделить пять зон, каждая из которых характеризуется определенной внутрен­ней структурой потока и в соответствии с этим определенной зависи­мостью λ от Re и k / d.

1. Зона изменения Rе от 0 до 2320. Ламинарный режим потока. Здесь 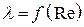. По Пуазейлю,

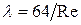                                             .                                                   (4)

2. Зона изменения Rе от 2320 до ~4000. Неустойчивая зона пере­межающейся турбулентности, когда на отдельных участках возникают области турбулентного режима, которые разрастаются, а затем исчезают и снова появляются. Изменение структуры потока сопровождается колебаниями величины λ. Зона не рекомендуется для применения в гидравлических системах.

3. Зона чисел Rе от ~4000 до ~10d / k. Поток характеризуется турбулентным ядром и пристенным (пограничным) ламинарным слоем, который затапливает шероховатости внутренней поверхности трубы, ввиду чего коэффициент λ не зависит от k / d и зависит только от Rе. Здесь трубы работают как «гидравлически гладкие». Для этой зоны, по Блазиусу,

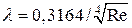                                                                                     (5)

4. Зона, в которой 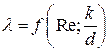. Пределы зоны определяются соотношением 10d / k<Rе<(500d)/ k. Переходная зона к «гидравличе­ски шероховатым» трубам. Пристенный ламинарный слой равен (или меньше) высоте выступов шероховатости.

5. Зона больших чисел Rе>(500d)/ k и, следовательно, интенсив­ной турбулентности. Трубы «гидравлически шероховатые». Коэффици­ент λ не зависит от Rе и является функцией только k / d.

Как показали более поздние исследования, результаты экспери­ментов Никурадзе для «гидравлически шероховатых» труб нельзя пере­нести на трубы с естественной шероховатостью. Оказалось, что в четвертой и пятой зонах общий характер зависимости (3) сохраняет­ся, но вид кривых на графике для различных типов шероховатостей получается различным, т. е. на λ влияет не только величина k / d, но и характер шероховатости стенок труб. Для реальных технических труб с естественной шероховатостью для определения λ в четвертой зоне может быть рекомендована формула Альтшуля

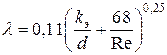                                      ,                                      (6)

а для пятой зоны — формула Шифринсона

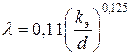                                                                                 (7)

Здесь k _э — эквивалентная абсолютная шероховатость, т. е. такая равно­мерная зернистая шероховатость Никурадзе, которая при расчетах дает такой же коэффициент λ, как и естественная шероховатость.

Отметим, что при малых Rе (<10d / k) формула (6) переходит в формулу (5) для гидравлически гладких труб, а при больших Rе (>500d / k) обращается в формулу (7) для вполне «гидравличе­ски шероховатых» труб.

Вместо расчетных формул (5), (6) и (7) для определения λ можно пользоваться графиком Г. А. Мурина.

Литература: [1, с. 95—106]; [2, с. 108—127]; [3, с. 74—82]; [4, с. 98—111]; [5, с. 226—265]; [6, с. 121 — 130]; [8, с. 37—38].

 

Вопросы для самопроверки

1. В чем отличие турбулентного течения от ламинарного? 2. Чем отличается распределение скоростей в цилиндрическом трубопроводе при ламинарном и турбулентном режимах движения жидкости? При каком режиме имеет место большая неравномерность скоростей и по­чему? 3. Объясните понятие «гладкие» и «шероховатые» поверхности. Может ли одна и та же труба быть «гидравлически гладкой» и «гид­равлически шероховатой»? В каком случае? 4. Объясните основные линии и зоны сопротивления на графике Никурадзе. 5. Какова зави­симость между потерей напора и средней скоростью течения жидкости в различных зонах и линиях на графике Никурадзе? 6.От каких факторов зависит коэффициент гидравлического трения при турбулент­ном течении и по каким формулам его можно определить? 7. Каковы особенности расчета потерь на трение по длине для некруглых трубо­проводов?

Методические указания

Местные сопротивления представляют собой короткие участки трубопроводов, на которых происходят изменения величины и направ­ления скоростей потока, вызванные изменением размеров и формы сечения трубопровода, а также направления его продольной оси. По­тери энергии в местных сопротивлениях, отнесенные к единице веса протекающей жидкости, называются местными потерями напора. Поте­ри в местных сопротивлениях делятся на потери трения и вихревые потери. Следует рассмотреть, как эти факторы проявляются в конкрет­ных местных сопротивлениях.

В общем случае коэффициент местного сопротивления 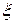 (в фор­муле для определения потерь в местных сопротивлениях) зависит от формы местного сопротивления, относительной шероховатости стенок, распределения скоростей в граничных сечениях потока перед местным сопротивлением и после него и от чисел Рейнольдса. Следует уяснить, как эта общая зависимость конкретизируется для различных зон тур­булентного течения и при ламинарном течении. Отметим, что в техни­ческих установках в большинстве случаев имеет место турбулентный режим, соответствующий пятой зоне квадратичного сопротивления, где коэффициент  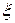не зависит от Rе и где проявляется автомодаль­ность. Если в трубопроводе до и после местного сопротивления имеет место ламинарный режим (жидкости с повышенной кинематической вязкостью), то в местных сопротивлениях, как правило, возникает тур­булентное течение.

Весьма существен вопрос о взаимном влиянии местных сопротив­лений. Простое суммирование потерь в местных сопротивлениях (так называемый принцип наложения потерь) дает правильные результаты, если сопротивления расположены друг от друга на расстоянии, пре­вышающем длину взаимного влияния, составляющую (30—40)d.

Литература: [1, с. 107—121]; [2, с. 128—146]; [3, с. 82—87]; [4, с. 111-117]; [5, с. 148-186]; [6, с. 139-150]; [8, с. 42-46].

 

Вопросы для самопроверки

1. Какие сопротивления называются местными? 2. По какой фор­муле определяются потери, вызванные местными сопротивлениями? 3. Как определить потерю напора при внезапном расширении трубо­провода? 4. В каком сечении берется средняя скорость, входящая в формулу потерь? 5. В чем принцип наложения потерь? 6. Как опреде­ляется коэффициент сопротивления системы трубопроводов (суммар­ный коэффициент сопротивления)?

Методические указания

Отверстие называется малым, если можно пренебречь изменением давления по его площади. Насадками называются небольшие по длине трубы ~ l=(3...6)d, присоединенные к таким отверстиям. Прежде всего, следует уяснить характер и особенности движения жидкости в процессе истечения (сжатые струи, образование вакуума).

В гидравлике истечения через отверстия и насадки есть много общего. Скорость истечения и вытекающий расход рассчитываются по общим формулам, выведенным на основе уравнения Бернулли, при­чем потери при истечении определяются как местные потери. Общими являются также гидравлические характеристики (коэффициенты рас­хода, скорости, сжатия, сопротивления).

Следует знать физический смысл коэффициентов сжатия, скорости и расхода, зависимость их числовых значений от типа и формы от­верстий и насадков и от критерия Рейнольдса. Нужно также обра­тить внимание на то, что при Re>10⁵  влияние сил вязкостного тре­ния на коэффициенты истечения практически отсутствует (квадратическая зона сопротивления). При этом коэффициенты истечения зави­сят только от формы отверстий и насадков. Это позволяет с успехом использовать отверстия с острой кромкой и с насадками в качестве измерителей расхода.

При истечении при переменном напоре (опорожнение сосудов) расчетными являются формулы для определения времени опорожне­ния.

Литература: [1. с. 122—136]; [2. с. 147— 185]; [3, с. 108—118]; [4, с. 146—162]; [5, с. 121—145]; [6, с. 171 — 177]; [8, с. 57—62].

 

Вопросы для самопроверки

1. Как связаны между собой коэффициенты сопротивления, сжа­тия, скорости и расхода? Поясните физический смысл этих коэффи­циентов. 2. В каком случае сжатие струи называется неполным, не­совершенным? Как неполнота и несовершенство сжатия влияют на коэффициент расхода? 3. Как рассчитываются затопленные отверстия и насадки? 4. Какое влияние оказывает вязкость жидкости при истече­нии из отверстий и насадков? 5. Как изменяются расход и скорость при истечении жидкости через цилиндрический насадок по сравнению с истечением ее из круглого отверстия того же диаметра и под тем же напором? 6. Чем отличается «насадок» от «трубы»? 7. В чем особен­ности истечения жидкости из большого отверстия по сравнению с исте­чением ее из малого отверстия?

Методические указания

Для гидравлического расчета трубопроводов применяются урав­нение Бернулли, формулы для определения потерь напора на трение по длине ив местных сопротивлениях, уравнение постоянства расхода.

Для нахождения различных гидравлических характеристик трубо­проводов применяются расчетные таблицы. К числу основных гидрав­лических характеристик относится расходная характеристика. В зависимости от гидравлической схемы работы и от методов гидравлического расчета различают трубопроводы короткие и длинные, простые и сложные, разветвленные и замкнутые, с транзитными и путевыми расходами жидкости. Следует уяснить различие между пере­численными типами трубопроводов и особенности их гидравлических расчетов. Все случаи расчета простых трубопроводов сводятся к трем типовым задачам по определению: 1) расхода, 2) напора, 3) диаметра трубопровода. Следует знать методику решения этих задач.

При расчете сложных трубопроводов составляется система урав­нений, которые устанавливают связь между размерами труб, расхода­ми жидкости и напорами. Эта система состоит из уравнений балан­са расходов для каждого узла и уравнений баланса напоров (урав­нений Бернулли) для каждой ветви трубопровода.

Литература: [1, с. 137—152]; [2. с. 204—225]; [3, с. 87—89]; [4, с. 117-140]; [5, с. 225-301]; [8, с. 48-52].

 

Вопросы для самопроверки

1. Какие трубопроводы называются короткими и длинными, прос­тыми и сложными? В чем особенности гидравлического расчета таких трубопроводов? 2. Изложите методику решения трех типовых задач расчета простого короткого трубопровода. 3. Какова особенность рас­чета трубопроводов с параллельным соединением линий? 4. Чем отлича­ется определение диаметра магистрального трубопровода и его от­ветвлений при расчете тупиковой водопроводной сети? 5. Что такое сифон и каковы особенности его гидравлического расчета? 6. В чем особенность расчета трубопроводов с насосной подачей жидкости?

Методические указания

Интегрирование дифференциального уравнения неустановившегося движения жидкости в напорном трубопроводе в предположении, что трубы обладают абсолютно жесткими стенками, а жидкость несжимае­ма, приводит к уравнению Бернулли с инерционным членом. Инерцион­ный член учитывает напор, затраченный на преодоление локальных сил инерции, т. е. сил инерции, обусловленных ускорением (или замедле­нием) всего объема жидкости в трубопроводе. В случае плавно изме­няющегося движения локальные ускорения определяются по изменению средних скоростей в сечениях потока. Для параллельно-струйного дви­жения (трубопровод постоянного сечения) локальное ускорение в каж­дый момент времени одинаково для всех сечений потока, т. е. жидкость условно представляется как твердое тело.

Если ускорения в потоке достаточно велики, то предположение о неупругости системы становится неприемлемым. Учет упругих свойств жидкости и стенок трубопровода приводит к рассмотрению процесса распространения вдоль трубопровода упругих волн деформации и свя­занных с ними волн резкого повышения и понижения давления, при­водит к явлению гидравлического удара.

Гидравлическим ударом называется повышение или понижение дав­ления в напорном трубопроводе, вызванное изменением во времени (в некотором сечении трубопровода) скорости движения жидкости. Явление гидравлического удара было теоретически и экспериментально изучено в конце XIX в. Н. Е. Жуковским в связи с многочисленными авариями московского водопровода.

Гидравлический удар чаще всего возникает в случае быстрого закрытия или открытия затвора, управляющего потоком в трубопро­воде. Различают прямой удар, когда время закрытия затвора меньше фазы гидравлического удара (время пробега ударной волны от затвора к резервуару и обратно), и непрямой удар, при котором время за­крытия затвора больше фазы гидравлического удара.

Формула Н. Е. Жуковского 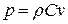 дает зависимость величины ударного повышения давления р от плотности жидкости ρ, скорости распространения ударной волны С, уменьшения скорости в трубе перед краном вследствие его закрытия v. Формула применима для расчета прямого и непрямого удара и учитывает как сжатие жидкости, так и растяжение стенок трубы при ударном повышении давления.

После уяснения физической сущности гидравлического удара и ме­тодов его расчета следует рассмотреть меры борьбы с ним.

Литература: [1, с. 153—164]; [2. с. 186—203]; [3. с. 99—106]; [4. с. 140—146]; [5. с. 305—378]; [8, с. 52—57].

 

Вопросы для самопроверки

1. Напишите формулу для определения инерционного напора. Объясните физический смысл входящих в нее величин. 2. Как изменится положение пьезометрической линии для трубы с постоянным диаметром при возникновении положительного и отрицательного локального уско­рения? 3. Что называется прямым и непрямым гидравлическим уда­ром? Что называется фазой гидравлического удара? Как она влияет на повышение давления при гидравлическом ударе? 4. Что такое ско­рость распространения ударной волны? От каких величин она зависит? 5. Чем гасится колебательный процесс, имеющий место при гидрав­лическом ударе? 6. Как можно уменьшить или предотвратить ударное повышение давления? 7. Что называется отрицательным гидравличе­ским ударом и когда он может возникнуть?

Методические указания

Настоящий раздел необходим для понимания принципа действия гидравлических машин, изучаемых во второй части курса. Следует хорошо разобраться в физической и механической сущности активного и реактивного взаимодействия между струей и твердой преградой, и сопротивлении твердых тел, движущихся в жидкости.

Литература: [1, с. 165—171]; [3, с. 118—128]; [4, с. 102—174]; [5, с. 376—406]; [8, с. 62—63].

Вопросы для самопроверки

1. Сформулируйте теорему об изменении количества движения. 2. Чему равна реактивная сила взаимодействия между струей и твер­дым телом? 3. Чему равно реактивное давление струи на плоскую стенку? на ковшеобразную стенку?

 

РАЗДЕЛ А. ЛОПАСТНЫЕ НАСОСЫ

 

Методические указания

Насосом называется гидравлическая машина, преобразующая механическую энергию двигателя в энергию перекачиваемой жидкости. В гидравлическом двигателе происходит преобразование энергии пото­ка жидкости в механическую энергию на выходном валу двигателя. Все типы насосов, несмотря на многообразие их конструктивных форм, по принципу действия, т.е. по способу передачи жидкости ме­ханической энергии, делятся на две группы: динамические (лопастные) и объемные (насосы вытеснения). К первым относятся центро­бежные, диагональные, осевые, вихревые насосы; ко вторым — порш­невые и роторные насосы.

При изучении этого раздела студент должен усвоить общую клас­сификацию насосов, их специфические особенности и область приме­нения.

При рассмотрении основных параметров насосов следует обратить внимание на определение напора, его физический смысл и действитель­ную размерность, надо также понять различие между полезной и за­траченной мощностями, разобраться в физическом смысле коэффициен­та полезного действия.

Литература: [1, с. 172—177]; [2, с. 226—227]; [4, с. 204—214]; [6. с. 183—184]; [9, с. 138—141].

 

Вопросы для самопроверки

I. Расскажите о принципе действия динамических и объемных насосов. 2. Как определяется напор действующего насоса по показа­ниям приборов и по элементам насосной установки? 3. Как определяет­ся полезная и затраченная мощность насоса? 4. Что представляет со­бой полный коэффициент полезного действия насоса?

 

Методические указания

Работа лопастных насосов основана на силовом взаимодействии лопастей с обтекающим их потоком. При вращении рабочего колеса в потоке жидкости возникает разность давлений по обе стороны каж­дой лопатки (подъемная сила). Силы давления лопастей на поток создают вынужденное вращательное и поступательное движения жид­кости, увеличивая ее давление и скоростной напор, т.е. механическую энергию.

Приращение энергии потока жидкости в лопастном колесе (напор насоса) зависит от сочетания скоростей протекания потока, частоты вращения колеса, его размеров, формы лопаток, т.е. от сочетания конструкции, размеров, частоты вращения и подачи насосов. Таким образом, главная особенность и отличие лопастных насосов от объем­ных состоят в том, что напор и подача у этих насосов взаимосвязаны, а подача непрерывна.

Созданная еще в середине XVIII в. Л. Эйлером приближенная струйная теория лопастных машин до настоящего времени является основой для их расчета. Сложность гидродинамических явлений, кото­рые возникают при протекании жидкости в рабочих органах насоса, привела к теоретической модели идеального рабочего колеса с беско­нечным числом бесконечно тонких лопастей. На основе струйной теории Л. Эйлером получено основное уравнение лопастных насосов, дающее зависимость теоретического напора от треугольников скоростей на выходе и входе рабочего колеса. С целью удовлетворительного согласования теории с данными опыта в формулу полезного (дейст­вительного) напора вводятся поправки на конечное число лопаток и на гидравлические потери. Следует обратить внимание на вывод ос­новного уравнения, которое может быть получено из уравнения Бернулли для относительного движения или из теоремы моментов коли­чества движения.

Различают теоретические и действительные характеристики ло­пастных насосов. Теоретические характеристики получаются в резуль­тате анализа основного уравнения лопастных насосов. Из-за слож­ности протекания жидкости через рабочие органы насоса точную взаи­мосвязь основных параметров работы насоса удается получить только экспериментально. В результате испытаний насосов получают их дейст­вительные характеристики — кривые зависимости напора, подачи, за­траченной мощности, КПД и частоты вращения насоса. Характеристики дают достаточно полное представление об эксплуатационных качест­вах насосов и позволяют решать вопросы, связанные с их эксплуата­цией и проектированием.

Студенту необходимо уяснить методику получения рабочих и уни­версальных характеристик, их использование для определения опти­мальных режимов работы действующих насосов, для выбора новых на­сосов, определения режимов совместной работы на общую сеть, а также для определения условий работы при изменении частоты вращения и размеров насоса.

При создании новых образцов лопастных машин проводятся их лабораторные исследования и доводка на моделях. Для перехода от данных, полученных на моделях, к натурным насосам используется общая теория гидродинамического подобия потоков в применении к ло­пастным машинам. Следует уяснить условия применимости теории по­добия к лопастным насосам, а также усвоить формулы пересчета основных параметров насосов при изменении размеров и частоты вращения.

При проектировании насосов одни и те же значения подачи и на­пора могут быть получены в насосах с различной частотой вращения. При этом конструктивный тип рабочего колеса и всей проточной час­ти насоса будет также различен. Для характеристики конструктивного типа насосов служит коэффициент быстроходности (удельная частота вращения), который определяет область применения насосов. Студенту следует знать, по какой формуле вычисляется коэффициент быстро­ходности, на какие типы подразделяются лопастные насосы в зависи­мости от его значения. Коэффициент быстроходности зависит не только от частоты вращения, но и от напора и подачи насоса. По­этому не всегда насосы с большей частотой вращения имеют больший коэффициент быстроходности.

Отрицательное влияние на работу центробежных насосов оказывает кавитация, возникающая в результате снижения давления при входе жидкости на рабочее колесо центробежного насоса ниже дав­ления парообразования. Студент должен знать физическую сущность влияния кавитации и меры, необходимые для избежания этого вред­ного явления.

Необходимо знать и уметь пользоваться формулой для определе­ния допустимой высоты всасывания центробежного насоса, определять навигационный запас по формуле Руднева.

Литература: [1, с. 177—254]; [2, с. 228—269]; [4, с. 226—257]; [6, с. 184—216]; [9, с. 141-186].

 

Вопросы для самопроверки

1. Начертите схему и объясните принцип действия одноступенча­того центробежного насоса. 2. Приведите параллелограммы скоростей на входе и выходе из рабочего колеса и поясните их. 3. Напишите ос­новное уравнение центробежных насосов Эйлера, поясните его вывод и физический смысл. 4. В чем заключаются соотношения подобия (про­порциональности) для лопастных машин? Для каких целей они при­меняются? 5. Что называется рабочей и универсальной характеристи­ками центробежных насосов? 6. На какие виды делятся лопастные насосы по быстроходности? 7. Как найти подачу и напор (рабочую точку) при работе одного и двух центробежных насосов на сеть? При­ведите соответствующие графики и характеристики. 8. Что такое осе­вое давление, как оно возникает и каковые меры его устранения (урав­новешивания)? 9. Какова физическая сущность явления кавитации в лопастных машинах. 10. Как влияет кавитация на работу центробежных насосов и каковы меры борьбы с ней? 11. Укажите методы регулирова­ния подачи центробежных насосов и расскажите об их физической сущности.

 

Вихревые и струйные насосы

Схема вихревого насоса, принцип действия, характеристика, об­ласти применения. Схема струйного насоса, принцип действия, области применения.

 

Методические указания

Рабочее колесо вихревого насоса имеет радиальные или наклонные лопатки и помещается в цилиндрическом корпусе с малыми торцевыми зазорами. Рабочий процесс вихревых насосов аналогичен центробеж­ным, однако имеет некоторые особенности. Напор вихревых насосов в 3...7 раз больше напора центробежных при тех же размерах и час­тоте вращения. Насосы имеют малый коэффициент быстроходности (6...40 об/мин) и применяются для больших напоров и малых расхо­дов. Они обладают способностью самовсасывания и могут перекачивать смеси жидкости и газа.

К струйным относятся насосы, рабочий процесс которых основан на эжектирующем действии струи рабочей жидкости (воды, газа, пара, воздуха). Насосы могут перекачивать воду, пульпу, нефть и другие жидкости, а также газы. Применяются для нагнетания (инжекторы), отсасывания (эжекторы) и вообще для перемещения жидкости (эле­ваторы). Ввиду сложности процессов расчет струйных насосов бази­руется главным образом на результатах экспериментов.

Нужно подробно рассмотреть рабочий процесс, характеристики, конструкции, способы регулирования и области применения вихревых и струйных насосов.

Литература: [I, с. 270—290]; [2, с. 269—271]; [4, с. 273—274]; [9, с. 220—224].

 

Вопросы для самопроверки

1. Начертите схемы вихревого и струйного насосов и расскажите о принципе их действия. 2. Какими достоинствами и недостатками обладают вихревые и струйные насосы? Какова область их примене­ния? 3. От чего зависит подача струйных насосов и как определяется их коэффициент полезного действия?

Общие понятия

Назначение и область применения гидродинамических передач. Принцип действия и классификация. Рабочая жидкость.

 

Методические указания

Гидродинамические передачи предназначены для передачи механи­ческой энергии с вала двигателя на вал приводной машины.

В практике эксплуатации машин-орудий все чаще требуется ис­кусственное приспособление характеристики двигателей к характерис­тикам приводных машин. С этой целью для изменения как частоты вращения, так и крутящего момента на валу приводной машины по сравнению с частотой вращения и крутящими моментами на валу дви­гателя применяются гидродинамические передачи.

Основными элементами гидродинамической передачи являются: рабочее колесо центробежного насоса — источник гидравлической энергии; рабочее колесо радиально-осевой или осевой гидротурбины — гидравлический двигатель; рабочая жидкость, а также реактор (на­правляющий аппарат), питающие и отводящие устройства.

В проточной части гидродинамической передачи при взаимодейст­вии лопастных систем с рабочей жидкостью происходит преобразова­ние механической энергии ведущего вала (двигателя) в механическую энергию рабочей жидкости, которая в свою очередь превращается в механическую энергию ведомого вала (приводной машины). По прин­ципу действия гидродинамические передачи делятся на два вида: гидро­динамические трансформаторы крутящего момента и гидродинамиче­ские муфты (сцепления). Следует рассмотреть ценные свойства гидро­динамических передач, которые определили применение их в различных областях техники.

В гидродинамических передачах в качестве рабочей жидкости применяются минеральное масло, вода, синтетические жидкости. Не­обходимо ознакомиться с требованиями, предъявляемыми к рабочим жидкостям, их физическими характеристиками, эксплуатационными свойствами, областью применения.

Литература: [1, с. 291-307]; [3, с. 230-232]; [6, 379-382]; [8. с. 68—80]; [9, с. 249—252].

 

Вопросы для самопроверки

1. Каковы назначение и область применения гидродинамических передач? На каких машинах и установках они применяются? Приведите примеры. 2. Изобразите принципиальные схемы гидротрансформатора и гидромуфты и поясните принцип их действия. 3. Каковы достоинства и недостатки гидродинамических передач? 4. Какие требования предъ­являются к рабочим жидкостям?

 

Гидродинамические муфты

Устройство и рабочий процесс. Основные параметры, уравнения и характеристики. Совместная работа гидромуфты с двигателем. Ре­гулирование гидромуфт.

 

Методические указания

Гидродинамическая муфта состоит из двух основных элементов: насосного и турбинного колес, которые крепятся соответственно на ведущем и ведомом валах. Замыкающий кожух, как правило, кре­пится к фланцу насосного колеса. Лопатки рабочих колес в большин­стве случаев плоские; радиальные. При вращении насосного колеса возникает силовое взаимодействие лопастей с обтекающим их потоком. При этом в потоке создается приращение момента количества движе­ния жидкости. Из насосного колеса жидкость поступает в турбинное колесо, где момент количества движения жидкости уменьшается, за счет чего на турбинном колесе возникает крутящий момент. Так как в гидромуфте отсутствуют устройства, способные изменить момент ко­личества движения жидкости в круге циркуляции, то увеличение мо­мента количества движения в насосном колесе всегда равно его умень­шению в турбинном колесе. Следовательно, если не учитывать меха­нические потери и потери трения о воздух, которые обычно малы, то в гидромуфте крутящий момент с ведущего вала на ведомый пере­дается без изменения.

Рабочий процесс в гидромуфте изложен здесь схематизировано. При его изучении следует рассмотреть треугольники скоростей на входе и выходе насосного и турбинного колес, проанализировать уравнения моментов количества движения. Следует уяснить, почему крутящий момент может передаваться, только когда частота вращения ведомого вала меньше частоты вращения ведущего (передаточное отношение меньше единицы), почему КПД гидромуфты равен передаточному отношению.

Оценка энергетических и эксплуатационных качеств гидромуфт мо­жет быть проведена с помощью характеристик. Различают внешние (моментные), универсальные и приведенные характеристики. Следует знать методику построения характеристик и уметь ими пользоваться при изучении работы гидромуфты в системе силовой трансмиссии.

Высокие эксплуатационные качества гидромуфт (гашение крутиль­ных колебаний и пульсаций крутящего момента, благоприятные ус­ловия запуска двигателя, ограничение передаваемого крутящего момента и пр.) определяется особенностями рабочего процесса и конст­руктивными особенностями гидромуфт.

Двигатель в сочетании с гидромуфтой представляет собой сило­вой агрегат, более полно удовлетворяющий требованиям приводной машины. Следует уяснить методику определения размеров гидромуф­ты (активного диаметра), методику построения выходной характерис­тики агрегата «двигатель — гидромуфта» и уметь пользоваться ею для анализа совместной работы гидромуфты с двигателем.

В эксплуатационной практике часто возникает необходимость из­менять частоту вращения ведомого вала гидромуфты, не изменяя пе­редаваемый крутящий момент, т. е. необходимость в регулировании гидромуфты. В зависимости от конструкции и назначения гидромуфт применяются различные способы их регулирования. Студенту необходи­мо знать наиболее распространенные способы регулирования, их физи­ческую сущность, достоинства и недостатки.

Литература: [1, с. 307-323]; [2, с. 339-345]; [3, с. 232-256]; [6, с. 382—390]; [8, с. 307—339]; [9, с. 252—255].

 

Вопросы для самопроверки

1. Поясните принцип и особенности работы гидромуфты. 2. При­ведите уравнение моментов для гидромуфты и поясните его. 3. Укажите соотношения подобия (пропорциональности). Для каких целей приме­няются эти соотношения? 4. Каковы преимущества и недостатки при­менения гидромуфты в системе силового привода? 5. Поясните метод построения выходной характеристики агрегата «двигатель — гидромуф­та». 6. Ответьте на 4-й вопрос, используя выходную характеристику агрегата с гидромуфтой. 7. Каково назначение регулирования гидро­муфты? Какие вам известны способы регулирования гидромуфты?

 

 

Методические указания

Гидротрансформатор отличается от гидромуфты тем, что в его проточной части кроме насосного и турбинного колес установлен не­подвижный реактор (направляющий аппарат). Лопастное колесо ре­актора, отклоняя своими лопатками жидкость изменяет момент коли­чества движения потока. Поэтому в гидротрансформаторе крутящие моменты на ведущем и ведомом валах не равны друг другу. Следовательно, гидротрансформаторы в отличие от гидромуфт являются пре­образователями крутящего момента.

Реактор размешается либо за турбинным колесом, либо за на­сосным. Как правило, имеется только одно насосное колесо. В зави­симости от степени трансформации крутящего момента гидротрансфор­маторы могут быть с одной или несколькими ступенями турбинных колес (не более трех) и могут иметь несколько реакторов. Разнообразие конструктивных схем позволяет строить гидротрансформаторы с различ­ными свойствами и характеристиками и подбирать их для эффективной работы в конкретных условиях силового привода.

К числу основных внешних параметров гидротрансформатора от­носятся крутящие моменты на ведущем и ведомом валах и на реакторе, передаточное отношение, КПД, коэффициент трансформации момен­тов. Функциональное графическое изображение этих параметров дает характеристики гидротрансформаторов. Различают внешние (моментные), универсальные и приведенные характеристики. Форма кривых на характеристиках зависит от профилирования лопаток рабочих колес, от количества и размещения рабочих колес в проточной части.

В зависимости от формы кривой крутящего момента на ведущем валу различают прозрачные и непрозрачные внешние (моментные) характеристики. Выбор гидротрансформаторов с различной прозрачно­стью характеристик диктуется условиями их работы: преобладанием требований надежности или экономичности силового привода.

Следует разобраться в методике построения характеристик, про­анализировать по характеристикам режимы работы гидротрансформа­торов при различных моментах на ведомом валу, которые определя­ются моментом сопротивления приводной машины, рассмотреть энерге­тические и эксплуатационные свойства гидротрансформаторов.

Гидротрансформатор обычно работает в системе силового при­вода. Экономичность и слаженность работы системы силового привода зависят от работы отдельных его элементов — двигателя, гидротранс­форматора и приводной машины и правильного согласования их друг с другом. Основой для согласования служат моментная характеристи­ка двигателя, приведенная характеристика гидротрансформатора и моментная характеристика приводной машины. Для согласования ха­рактеристик используются формулы подобия и уравнение момента гид­родинамических передач.

Следует рассмотреть методику выбора размера гидротрансформа­тора (активного диаметра), построения выходной характеристики агре­гата «двигатель — гидротрансформатор» и уметь ими пользоваться для анализа работы гидротрансформатора в системе силового при­вода.

В комплексных гидротрансформаторах реактор размещается на муфте свободного хода и при некоторых режимах может вращаться вместе с рабочими колесами. Следует рассмотреть назначение таких гидротрансформаторов, их характеристики и эксплуатационные свой­ства.

Литература: [1, с. 323-335]; [2, с. 339-345]; [3, с. 232-238; 256—259]; [6, с. 390-398]; [8, с. 340-348]; [9, с. 255-258].

 

Вопросы для самопроверки

1. Поясните принцип действия и особенности работы гидротранс­форматора. 2. Чем отличаются прозрачные характеристики гидро­трансформатора от непрозрачной? Для каких условий работы они при­меняются? 3. Поясните метод выбора размеров гидротрансформатора и согласование характеристик элементов силового привода. 4. Каковы конструктивная схема, моментная характеристика и назначение комплексного гидротрансформатора? б. Какие применяются способы ре­гулирования гидротрансформаторов?

 

Общие положения

Объемные насосы, принцип действия, общие свойства и классифи­кация.

 

Методические указания

В объемных насосах передача механической энергии жидкости осуществляется изменением объемов их рабочих камер. Объемные насо­сы делятся на классы:

1) поршневые — с возвратно-поступательным движением вытеснителя (поршня или плунжера) и клапанным рас­пределением жидкости;

2) роторные — с вращательным движением вытеснителей или замыкателей (например, поршней плунжеров, зубьев шестерен, лопаток или пластин) и с бесклапанным распределением жидкости.

В отличие от лопастных насосов в объемных насосах жидкости сообщается потенциальная энергия давления при практически неиз­менной кинетической энергии жидкости. В этих насосах подача и на­пор независимы друг от друга, насосы характеризуются неравномер­ностью подачи и пульсацией давлений.

Литература: [1, с. 336—342]; [2. с. 272-274]; [3. с. 155-157]; [4, с. 204—214]; [6, с. 256-272]; [8, с. 81-90]; [9, с. 5—7].

 

Вопросы для самопроверки

1. Расскажите о принципе действия объемных насосов. 2. Приведи­те примеры объемных насосов и укажите элементы, присущие объем­ным насосам всех типов. 3. Каковы преимущества и недостатки, присущие объемным насосам всех типов?

 

Методические указания

Поршневой насос представляет собой гидравлическую машину, в которой преобразование механической энергии двигателя в механиче­скую энергию перемещаемой жидкости осуществляется при помощи поршня или плунжера, совершающего возвратно-поступательное дви­жение в цилиндре. Поршневые насосы принадлежат к классу объемных насосов. Они классифицируются по кратности действия, устройству поршня, расположению цилиндров, способу соединения поршня с дви­гателем, по быстроходности (числу двойных ходов), по развиваемому давлению. Студент должен знать принцип действия насосов, уметь изобразить и пояснить принципиальные схемы насосов одинарного, двойного, дифференциального действия и др.

Подача поршневых насосов пропорциональна их размерам (объ­ему, вытесняемому поршнем при его движении на нагнетание), а также скорости движения поршня (числу двойных ходов — или числу оборотов в единицу времени). Напор поршневых насосов не связан с подачей и зависит от сопротивлений (геодезический напор, гидравли­ческие сопротивления), которые он должен преодолевать.

Одной из основных особенностей поршневых насосов является неравномерная подача жидкости по времени. Студент должен знать способ построения графиков мгновенной подачи и уметь вывести чис­ловые значения коэффициента неравномерности подачи для насосов различной кратности действия. Следует рассмотреть влияние клапан­ного распределения жидкости на характеристики и свойства поршне­вых насосов.

Для улучшения равномерности подачи на всасывающем и напор­ном патрубках насоса устанавливаются воздушные колпаки. При рас­смотрении работы воздушных колпаков необходимо понять, почему ус­тановка колпака на всасывающем патрубке позволяет увеличить вы­соту всасывания и число двойных ходов насоса, а установка колпака на напорном патрубке сглаживает неравномерность подачи жидкости к потребителю.

Важной характеристикой работы насоса является индикаторная диаграмма, представляющая собой кривую изменения давления в ка­мере насоса за один двойной ход поршня. Индикаторная диаграмма позволяет судить о качестве насоса, влиянии воздушных колпаков на процессы всасывания и нагнетания, дает возможность установить наличие! тех или иных нарушений в работе насоса, позволяет уточнить баланс мощности и КПД в насосе.

Литература: [1, с. 343—354); [2, с. 274—276]; [3, с. 157—166]; [4, с. 214—226]; [6, с. 272—289]; [8, с. 115—117]; [9, с. 8—49].

                

Вопросы для самопроверки

1. Приведите схемы и объясните принцип действия поршневых насосов одинарного, двойного, дифференциального действия. 2. От чего зависит и по каким формулам определяется производительность насо­сов различной кратности действия? Что такое объемный КПД насо­са? 3. Приведите графики мгновенной подачи поршневых насосов оди­нарного и двойного действия; объясните метод их построения и гид­равлическую сущность; укажите способы уменьшения неравномерности подачи. 4. Изобразите индикаторную диаграмму поршневого насоса и объясните ее. В чем отличие действительной индикаторной диаграммы от идеальной. 5. От чего зависит и как определяется высота всасыва­ния поршневых насосов? Укажите способы увеличения высоты всасы­вания. 6. Каковы преимущества и недостатки поршневых насосов по сравнению с центробежными? 7. Как регулируется подача поршневых насосов и каковы правила их пуска?

 

Методические указания

Роторными называются объемные насосы вращательного движения, содержащие статор, ротор и замыкатели, герметично соприкасающиеся со статором и ротором и разделяющие приемную камеру от нагнета­тельной. По конструкции роторные насосы разделяют на роторно-поршневые (радиальные и аксиальные), пластинчатые (шиберные, шестеренные, винтовые). Эти насосы широко используются в объемных гидравлических приводах. Роторные насосы обратимы, т. е. могут работать в качестве насосов и гидромоторов, имеют бесклапанное распре­деление жидкости и потому выполняются быстроходными, имеют мень­шую неравномерность подачи, чем поршневые насосы, могут быть вы­полнены с регулированием и реверсированием подачи (роторнопоршневые насосы и шиберные простого действия).

Роторные насосы, так же как и поршневые, не могут работать с закрытой задвижкой и, как правило, снабжаются предохранитель­ным клапаном, разгружающим насос в случае перегрузки. Студенту необходимо разобраться в принципе действия и устройстве перечис­ленных типов роторных насосов. Следует знать область их применения, принцип действия, кинематическую схему, уметь объяснить конструк­тивную схему, знать формулы для определения подачи насоса и рабо­чего объема и способы регулирования подачи, характеристики.

Обращенные роторные насосы являются гидромоторами враща­тельного действия. Так же как и насосы, они могут быть регулируе­мыми и нерегулируемыми, реверсивными и нереверсивными.

При изучении роторных гидромоторов следует усвоить принцип действия и устройство, расчетные формулы для определения крутя­щего момента, мощности, частоты вращения. Следует обратить вни­мание на способы изменения (регулирования) этих параметров в слу­чае нерегулируемых и регулируемых гидромоторов.

Литература: [1, с. 354—403]; [2, с. 276—301]; [3. с. 166—172, 175—184]; [4, с. 257—271, 308—309]; [6, с. 289—316]; [7, с. 126— 244]; [8, с. 90—114, 119-162]; [9, с. 113—137].

Вопросы для самопроверки

1. Приведите конструктивные схемы и объясните принцип дейст­вия радиально- и аксиально-поршневых, пластинчатых (шиберных), шестеренных и винтовых насосов. 2. Напишите формулы для опреде­ления подачи роторных насосов и объясните их. Изменением каких параметров осуществляется регулирование подачи насоса? 3. Каковы достоинства и недостатки роторных насосов? 4. Укажите область при­менения роторных насосов. 5. На схемах роторно-поршневых гидро­моторов рассмотрите кинематическую цепочку трансформации усилий на поршнях, создаваемых рабочей жидкостью, и механический момент на валу гидромотора. 6. От каких параметров зависят развиваемые на валу роторных гидромоторов крутящий момент, мощность и частота вращения? Приведите соответствующие формулы для каждого типа гидромотора и поясните их. 7. Расскажите о принципе действия и конструктивных особенностях высокомоментных гидромоторов;

 

Гидроцилиндры

Силовые гидроцилиндры, их назначение и устройство. Поворот­ные гидроцилиндры.

 

Методические указания

Силовые гидравлические цилиндры являются гидравлическими дви­гателями возвратно-поступательного действия, работающими по прин­ципу обращенных поршневых насосов. В отличие от последних сило­вые гидроцилиндры не имеют клапанов. Студенту необходимо рассмот­реть конструктивные схемы гидроцилиндров одностороннего и двустороннего действия и телескопических, усвоить расчетные формулы для определения усилия на штоке, скорости движения поршня, потребной подачи >жидкости, развиваемой мощности с учетом полного и частных КПД гндроцилиндра.

Литература: [1, с. 403—410]; [3, с.'172—175]; [4, с. 307—308]; [7, с. 318—328]; [8, с. 162—176].

 

Вопросы для самопроверки

1. Приведите схемы силовых гидроцилиндров одностороннего и двустороннего действия и поясните их. 2. Как определить потребную подачу для гидроцилиндров одностороннего и двустороннего действия? Как влияет объемный КПД на подачу? 3. От каких параметров гидроцилиндров зависят развиваемые мощность и усилие на штоке? Приведите соответствующие формулы и поясните их.

 

Основные понятия и элементы гидропривода

Принцип действия объемного гидропривода. Классификация объ­емных гидроприводов по характеру движения выходного звена и дру­гим признакам. Основные элементы гидропривода.

 

Методические указания

Объемный гидропривод предназначен для передачи при помощи объемных гидромашин механической энергии двигателя к исполнитель­ным механизмам с преобразованием скоростей и сил или моментов.

Объемный гидропривод содержит объемный насос (источник гид­равлической энергии), объемные гидромоторы (приемники гидравличе­ской энергии или исполнительные механизмы), гидроаппаратуру (уст­ройства или механизмы, предназначенные для передачи энергии, управ­ления и регулирования).

В зависимости от типа гидродвигателя (силовой гидроцилиндр или роторный гидромотор) различают гидроприводы возвратно-посту­пательного и вращательного движения выходного звена. Схема гидропривода может быть открытой (с аккумулирующим рабочую жидкость баком) и закрытой (бак отсутствует, давление в системе больше атмо­сферного). Закрытая схема не применяется при наличии гидроци­линдров.

Литература: [I. с. 411—412]; [2, с. 302—305]; [3, с. 141 — 155]; [4, с. 290—296]; [6, с. 354—360]; [7, с. 8—12]; [с. 68—80]

 

Вопросы для самопроверки

1. Из каких основных частей состоит объемный гидропривод? При­ведите одну из известных конструктивных схем и поясните ее. 2. Что такое открытая и закрытая схемы объемного гидропривода? Приведите схемы, объясните принцип действия и укажите преимущества и не­достатки. 3. Укажите достоинства и недостатки объемного гидро­привода.

 

Методические указания

Распределительные устройства предназначены для направления и распределения потока рабочей жидкости от насоса к гидромоторам и отвода от них отработавшей жидкости на слив.

Различают пробковые, золотниковые и клапанные распределитель­ные устройства. Наиболее распространены золотниковые распредели­тельные устройства, так как они сравнительно просты в изготовлении, компактны, надежны в работе, позволяют распределять большие по­токи жидкости. По функциональным признакам клапаны делятся на предохранительные, обратные, редукционные.

Для регулирования объемного гидропривода применяются дроссе­ли, представляющие собой регулируемое сопротивление, площадь проходного отверстия которого можно изменять в процессе работы гидропривода. В зависимости от вида проходного отверстия дроссели де­лятся на игольчатые, щелевые, канавочные и пластинчатые.

Следует знать принцип действия и конструктивные особенности механизмов, а также их место и условия работы в общей схеме гидропривода. Следует изучить условные обозначения всех элементов объемного гидропривода.

Литература: [1, с. 418-458, 472-499]; [2, с. 317-334]; [3, с. 184-211]; [4, с. 309-318]; [7, с. 329-454]; [8, с. 194-248].

                               

Вопросы для самопроверки

1. Приведите конструктивную схему золотникового распределителя и его условное изображение по ГОСТу и поясните, как осуществляется подача рабочей жидкости к гидромотору. 2. Поясните принцип дей­ствия и конструкцию клапанов различного назначения. Приведите фор­мулы для их расчета. 3. По какой формуле определяется расход ра­бочей жидкости через дроссель? При помощи каких устройств обеспе­чивается постоянство перепада давления на дросселе? 4. Для каких целей в системах гидропривода применяются фильтры и гидроаккуму­ляторы?

 

Методические указания

Для изменения частоты вращения вала роторного гидромотора или скорости перемещения поршня силового гидроцилиндра применяют дроссельное или объемное регулирование.

Дроссельное регулирование осуществляется регулируемым сопро­тивлением (дросселем), которое устанавливается на входе, на выходе или параллельно гидромотору. В первом и втором случаях часть жидкости от насоса идет на слив через переливной клапан, давление за насосом определяется настройкой клапана, а насос всегда работает с максимальной подачей. В третьем случае давление за насосом оп­ределяется нагрузкой на гидромотор, клапан работает как предохра­нительный, и только тогда, когда давление превысит допустимый пре­дел, потребляемая мощность будет пропорциональна нагрузке. Таким образом, третий случай более экономичен.

Все три схемы расположения дросселя не обеспечивают постоян­ства скорости при изменении нагрузки, так как при этом перепад давления на дросселе не остается постоянным. Для создания «жест­кой» характеристики, когда требуется, чтобы скорость не зависела ОТ нагрузки, вместе с дросселем применяются регуляторы перепада Давления на дросселе (регуляторы скорости).

Объемное регулирование осуществляется изменением рабочего объ­ема насоса или гидромотора или обоих вместе. Регулирование высоко­качественное, происходит практически без потерь, но для его осуществ­ления необходимы сложные по конструкции и дорогие в изготовлении регулируемые гидромашины.

Следует рассмотреть основные схемы с дроссельным и объемным регулированием, разобраться в их работе и взаимодействии узлов и ме­ханизмов, уяснить преимущества и недостатки и область применения.

Литература: [1, с. 412—417]; [2, с. 302—309]; [3, с. 211—230]; [4, с. 297—306, 333—357]; [6, с. 360—379]; [8, с. 249—282].

 

Вопросы для самопроверки

1. Какими способами осуществляется бесступенчатое регулирова­ние частоты вращения или перемещения рабочего органа гидропри­вода? 2. Каковы особенности дроссельного регулирования при различ­ном расположении дросселя в схеме гидропривода? 3. Укажите отно­сительные преимущества и недостатки дроссельного и объемного ре­гулирования. В каких случаях они применяются? 4. По конкретным схемам гидропривода с объемным и дроссельным регулированием рас­скажите о взаимодействии всех элементов системы в процессе регу­лирования.

 

Следящий гидропривод

Назначение, принципы действия, схема и область применения сле­дящего гидропривода.

 

Методические указания

Следящим гидроприводом, или гидроусилителем, называется устройство, в котором исполнительный двигатель (выход) автомати­чески и непрерывно воспроизводит движение задающего устройства (входа) при требуемом усилении выходной мощности двигателя за счет использования энергии подаваемой жидкости. Принцип действия гидроусилителя основан на том, что изменение положения задающего устройства (ручки управления или элемента автоматики) приводит к рассогласованию системы, а вызванное им действие исполнительного двигателя устраняет рассогласование, приводя выходное звено к поло­жению задающего устройства. Различают следящий привод без об­ратной связи (разомкнутый) и с обратной связью (замкнутый), прерывистого (импульсного) и непрерывного (пропорционального) деист.. вия.

Следует рассмотреть конкретные схемы следящих гидроприводов различного типа, конструктивные схемы механизмов и устройств, со­ставляющих гидропривод, область применения, преимущества и недостатки по сравнению, например, с электрическими следящими систе­мами.

Литература: [1, с. 459-471]; [2, с. 309—318]; [7, с. 455-512].

 

Вопросы для самопроверки

1. Для каких целей применяется следящий гидропривод? 2. Из каких механизмов и устройств состоит следящий гидропривод? 3. По конкретной схеме следящего гидропривода расскажите о принципе его работы, устройстве отдельных элементов, его характеристике.

  

 

КОНТРОЛЬНЫЕ ЗАДАНИЯ

В зависимости от специальности и учебного плана контрольное задание может состоять из одной, двух или трех контрольных работ, в каждую из которых входит определенное количество контрольных задач (табл. 1).

Одна контрольная работа выполняется студентами-заочниками специальностей «Технология и комплексная механизация подземной разработки месторождений полезных ископаемых» (0202); «Технология и комплексная механизация открытой разработки месторождений по­лезных ископаемых» (0209).

Две контрольные работы выполняются студентами-заочниками следующих специальностей: «Технология и комплексная механизация разработки торфяных месторождений» (0203), «Обогащение полезных ископаемых» (0204), «Машины и оборудование нефтяных и газовых промыслов» (0508); «Автоматизация и комплексная механизация ма­шиностроения» (0636); «Технология деревообработки» (0902).

Студенты-заочники специальностей «Судовые машины и механиз­мы» (0524) и «Лесоинженерное дело» (0901) выполняют три контроль­ные работы.

Номера контрольных задач выбираются согласно последней цифре шифра зачетной книжки студента (см. табл. 1), числовые значения указанных в задаче величин — по предпоследней цифре шифра зачет­ной книжки студента (табл. 2).

 

Таблица 1. Номера задач в контрольных работах

Последняя цифра шифра зач. книжки	При выполнении одной контрольной работы
0	1, 7, 10, 19, 22
1	2, 8, 11, 20, 23
2	3, 9, 12, 21, 24
3	4, 7, 13, 19, 25
4	5, 8, 14, 20, 26
5	6, 9, 15, 21, 27
6	1, 7, 16, 19, 22
7	2, 8, 17, 20, 23
8	4, 19, 18, 21, 24
9	6, 8, 13, 20, 24

ЗАДАЧИ

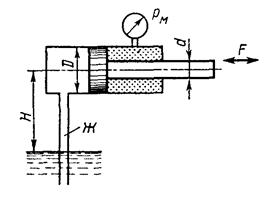
1. Определить величину и направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня нахо­дится воздух, слева от поршня и в резервуаре, куда опущен открытый конец трубы, — жидкость Ж (рис. 1). Показание пружинного мано­метра — р_м.

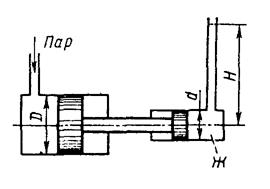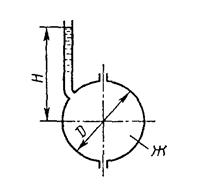
2. Паровой прямодействующий насос подает жидкость Ж на вы­соту Н (рис. 2). Каково абсолютное давление пара, если диаметр парового цилиндра D, а насосного цилиндра d? Потерями на трение пренебречь.

          Рис. 1                                                          Рис. 2

3. Определить силу прессования F, развиваемую гидравлическим прессом, у которого диаметр большего плунжера - D, диаметр меньшего плунжера – d. Больший плунжер расположен выше меньшего на величину Н; рабочая жидкость – Ж, усилие, приложенное к рукоятке, - R (рис. 3).

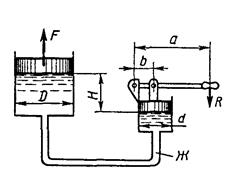
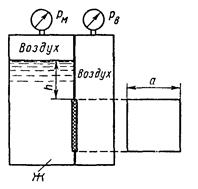
4. Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а, закрытое крышкой (рис. 4). Давление над жидкостью Ж в левой части резервуара определяется показаниями манометра p _м, давление воздуха в правой части – показания мановакуумметра. Определить величину и точку приложения результирующей силы давления на крышку.

Указание. Эксцентриситет e центра давления для результирующей силы может быть определен по выражению

,

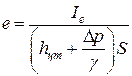где

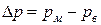
    Рис. 3                                                                       Рис. 4                     

5. Шар диаметром D наполнен жидкостью Ж. Уровень жидкости в пьезометре, присоединенном к шару, установился на высоте H от оси шара. Определить силу давления на боковую половину внутренней поверхности шара (рис. 5). Показать на чертеже вертикальную и го­ризонтальную составляющие, а также полную силу давления.

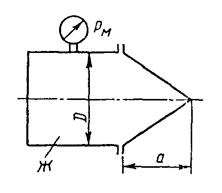6. Определить силу давления на коническую крышку горизонталь­ного цилиндрического сосуда диаметром D, заполненного жидкостью Ж (рис. 6). Показание манометра в точке его присоединения - p _м. Показать на чертеже вертикальную и горизонтальную составляющие, а также полную силу давления.

                Рис. 5                                                                       Рис. 6

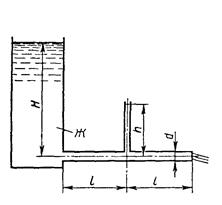
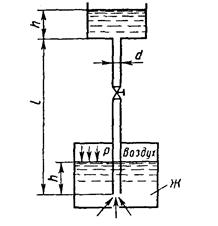
7. При истечении жидкости из резервуара в атмосферу по гори­зонтальной трубе диаметра d и длиной 2 l уровень в пьезометре, уста­новленном посередине длины трубы, равен h (рис. 7). Определить рас­ход Q и коэффициент гидравлического трения трубы λ, если статиче­ский напор в баке постоянен и равен Н. Построить пьезометрическую и напорную линии. Сопротивлением входа в трубу пренебречь.

8. Жидкость Ж подается в открытый верхний бак по вертикальной трубе длиной l и диаметром d за счет давления воздуха в нижнем замкнутом резервуаре (рис. 8). Определить давление р воздуха, при котором расход будет равен Q. Принять коэффициенты сопротивления: вентиля 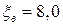; входа в трубу 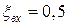; выхода в бак 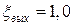. Экви­валентная шероховатость стенок трубы  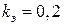мм.

           Рис.7                                                                     Рис.8

9. Поршень диаметром D движется равномерно вниз в цилиндре, подавая жидкость Ж в открытый резервуар с постоянным уровнем (рис. 9). Диаметр трубопровода d, его длина l. Когда поршень нахо­дится ниже уровня жидкости в резервуаре на Н=0,5 м, потребная для его перемещения сила равна F. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометри­ческую линии для трубопровода. Коэффициент гидравлического трения трубы принять 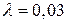. Коэффициент сопротивления входа в трубу 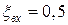. Коэффициент сопротивления выхода в резервуар .

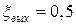10. Определить диаметр трубопровода, по которому подается жид­кость Ж с расходом Q, из условия получения в нем максимально возможной скорости при сохранении ламинарного режима. Темпера­тура жидкости t=20°С.

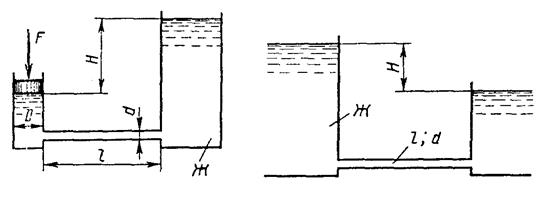
                  Рис. 9                                                  Рис. 10

11. При ламинарном режиме движения жидкости по горизонталь­ному трубопроводу диаметром d=30 см расход равнялся Q, а паде­ние пьезометрической высоты на участке длиной l составило h. Опре­делить кинематический и динамический коэффициенты вязкости пере­качиваемой жидкости.

12. По трубопроводу диаметром d и длиной l движется жид­кость Ж (рис. 10). Чему равен напор H, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учиты­вать. Температура жидкости t=20ºС.

Указание. Воспользоваться формулой для потерь на трение при ламинарном режиме (формула Пуазейля).

13. На поршень диаметром D действует сила F (рис. 11). Опре­делить скорость движения поршня, если в цилиндре находится вода, диаметр отверстия в поршне d, толщина поршня a. Силой трения поршня о цилиндр пренебречь, давление жидкости на верхнюю плос­кость поршня не учитывать.

14. Определить длину трубы l, при которой расход жидкости из бака будет в два раза меньше, чем через отверстие того же диамет­ра d. Напор над отверстием равен Н. Коэффициент гидравлического трения в трубе принять 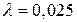 (рис. 12).

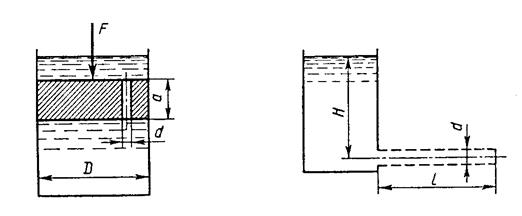
           Рис. 11                                                  Рис. 12      

15. Определить длину трубы l, при которой опорожнение цилиндрического бака диаметром D на глубину H будет происходить в два раза медленнее, чем через отверстие того же диаметра d. Коэффициент гид­равлического трения в трубе принять 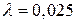 (рис. 12).

Указание. В формуле для определения времени опорожнения бака коэффициент расхода µ выпускного устройства определяется его конструкцией. Для трубы

.

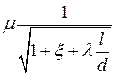где 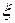  — суммарный коэффициент местных сопротивлений.

16. Определить диаметр горизонтального стального трубопрово­да d длиной l=20 м, необходимый для пропуска по нему воды в коли­честве Q, если располагаемый напор равен H. Эквивалентная шеро­ховатость стенок трубы k=0,15 мм.

Указание. Для ряда значений d и заданного Q определяется ряд значений потребного напора H _п. Затем строится график H _п = f ( d ), и по заданному H определяется D.

17. Из бака А, в котором поддерживается постоянный уровень, вода протекает по цилиндрическому насадку диаметром d в бак В, из которого сливается в атмосферу по короткой трубе диаметром D, снабженной краном (рис. 13). Определить наибольшее значение коэф­фициента сопротивления крана 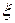, при котором истечение из насадка будет осуществляться в атмосферу. Потери на трение в трубе не учи­тывать.

18. При внезапном расширении трубопровода скорость жидкости в трубе большего диаметра равна v. Отношение диаметров труб D / d=2 (рис. 14). Определить h — разность показаний пьезометров.

                 Рис. 13                                                          Рис. 14

19. Горизонтальная труба служит для отвода жидкости Ж в коли­честве Q из большого открытого бака (рис. 15). Свободный конец трубы снабжен краном. Определить ударное повышение давления в трубе перед краном, если диаметр трубы d, длина l, толщина стенки 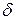, материал стенки — сталь. Кран закрывается за время t _зак по закону, обеспечивающему линейное уменьшение скорости жидкости в трубе перед краном в функции времени.

20. Вода в количестве Q перекачивается по чугунной трубе диа­метром d, длиной l с толщиной стенки δ. Свободный конец трубы снаб­жен затвором. Определить время закрытия затвора при условии, чтобы повышение давления в трубе вследствие гидравлического удара не превышало 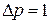МПа. Как повысится давление при мгновенном закрытии затвора?

21.Определить время закрытия задвижки, установленной на сво­бодном конце стального водопровода диаметром D, длиной l, с толщи­ной стенки δ, при условии, чтобы максимальное повышение давления в водопроводе было в три раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия задвиж­ки повышение давления распространится до сечения, находящегося на расстоянии 0,7 l от задвижки?            

22. Центробежный насос производительностью Q работает при час­тоте вращения n (рис. 16). Определить допустимую высоту всасывания, если диаметр всасывающей трубы d, а ее длина l. Коэффициент кави­тации n в формуле Руднева принять равным С. Температура воды t=20°С. Коэффициент сопротивления колена 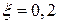. Коэффициент сопротивления входа в трубу 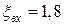. Эквивалентная шероховатость стеной трубы k _э=0,15 мм.

         Рис. 15                                           Рис. 16

23. Центробежный насос подает воду в количестве Q из колодца в открытый напорный бак по трубе диаметром d на геодезическую высоту Н. Определить коэффициент быстроходности и коэффициент полезного действия насоса, если мощность на валу насоса N_e, частота вращения n, а суммар­ный коэффициент сопротивления системы (сети) .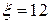

24. Вода перекачивается насосом I из откры­того бака в расположенный ниже резервуар В, где поддерживается постоянное давление р_в, по трубопроводу общей длиной l и диаметром d. Разность уровней воды в баках h (рис. 17). Определить напор, создаваемый насосом для по­дачи в бак В расхода воды Q. Принять суммар­ный коэффициент местных сопротивлений 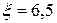. Эквивалентная ше­роховатость стенок трубопровода k _э=0,15 мм.

25. Определить производительность и напор насоса (рабочую точку) при подаче воды в открытый резервуар из колодца на геоде­зическую высоту H по трубопроводу диаметром d, длиной l с коэффи­циентом гидравлического трения λ=0,03 и эквивалентной длиной мест­ных сопротивлений l _экв=8 м.

Как изменяется подача и напор насоса, если частота вращения рабочего колеса уменьшится на 10%?  

Данные, необходимые для  построения характеристики Q —Н центробежного насоса:

Q	0	0,2Q0	0,4Q0	0,6Q0	0,8Q0	1,0Q0
H	1,0H0	1,05H0	1,0H0	0,88H0	0,65H0	0,35H0

26. Два одинаковых насоса работают параллельно и подают воду в открытый резервуар из колодца на геодезическую высоту Н по трубопроводу диаметром d, длиной l, с коэффициентом гидравлического трения 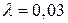 и суммарным коэффициентом местных сопротивлений 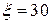. Определить рабочую точку (подачу и напор) при совместной работе насосов на сеть. Как изменятся суммарная подача и напор, если частота вращения рабочего колеса одного из насосов увеличится на

10%? (Данные, необходимые для построения характеристик Q - H те же, что и в задаче 25).

Рис. 17

27. Два одинаковых насоса работают последовательно и подают воду в открытый резервуар из колодца на геодезическую высоту Н_г. Определить рабочую точку (подачу и напор) при совместной работе насосов на сеть, если коэффициент сопротивления сети (системы) - 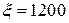, а диаметр трубопровода - d. Как изменятся суммарный напор и подача, если частота вращения рабочего колеса одного из насосов увеличится на 12%? (Данные, необходимые для построения характеристик Q - H те же, что и в задаче 25).

28. Определить средний объемный коэффициент полезного действия, максимальную теоретическую подачу и степень неравномерности подачи поршневого насоса двойного действия с диаметром цилиндра D, ходом поршня S и диаметром штока d при n двойных ходах в минуту, заполняющего мерный бак емкостью W в течение t _с.

29. Поршневой насос двойного действия подает воду в количестве Q из колодца в открытый резервуар на геодезическую высоту Н_г по трубопроводу длиной l, диаметром d; коэффициент гидравлического трения 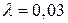 и суммарный коэффициент местных сопротивлений 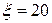. Определить диаметр цилиндра и мощность электродвигателя, если отношение длины хода поршня к его диаметру S / D=1; число двойных ходов в минуту n, отношение диаметра штока к диаметру поршня d / D=0,15; объемный коэффициент полезного действия 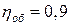; полный коэффициент полезного действия .

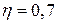30. Поршневой насос простого действия с диаметром цилиндра D, ходом поршня S, числом двойных ходов в минуту n и объемным КПД 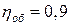 подает рабочую жидкость в систему гидропривода. При какой частоте вращения должен работать включенный параллельно шестеренный насос с начальным диаметром шестерен d _н, шириной шестерен b, числом зубьев z=30 и объемным КПД 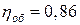, чтобы количество подаваемой жидкости удвоилось?

31. Силовой гидравлический цилиндр (рис. 18) нагружен силой F и делает n двойных ходов в минуту. Длина хода поршня S, диаметр поршня D, диаметр штока d. Определить давление масла, потребную подачу и среднюю скорость поршня. Механический КПД гидроцилиндра 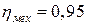, объемный КПД .

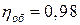32. Перемещение поршней гидроцилиндров с диаметром D=25см осуществляется подачей рабочей жидкости (v=1,5 см²/с, 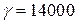Н/м³) по трубам 1 и 2 одинаковой эквивалентной длины l=20 м и диаметром d=5 см (рис. 19). Определить силу F ₂, при которой скорость перемещения второго поршня была бы в два раз больше скорости первого поршня. Расход магистрали – Q, первый поршень нагружен силой F ₁.

Указание. На перемещение поршней затрачивается одинаковый ударный напор (считая от точки А).

               Рис.18                                                          Рис. 19

33. Перемещение поршней гидроцилиндров с диаметром D=20 см, нагруженных силами F ₁ и F ₂, осу­ществляется подачей минерального масла по трубам 1 и 2 с одинако­выми диаметрами d=4 см (рис. 19). Суммарный коэффициент сопротив­ления первого трубопровода 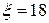. Каким должен быть суммарный ко­эффициент сопротивления второго трубопровода, чтобы при расходе Q в магистрали скорости поршней бы­ли одинаковыми?

Указание. На перемещение поршней затрачивается одинаковый суммарный напор, считая от точ­ки А.

34. Определить полезную мощность насоса объемного гидропри­вода, если внешняя нагрузка на поршень силового гидроцилиндра F, скорость рабочего хода v, диаметр поршня D ₁, диаметр штока D ₂ (рис. 20). Механический коэффициент полезного действия гидроци­линдра 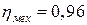, объемный коэффициент полезного действия гидро­цилиндра 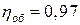. Общая длина трубопроводов системы l; диаметр трубопроводов d; суммарный коэффициент местных сопротивлений 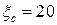. Рабочая жидкость в системе — спиртоглицериновая смесь ( 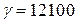Н/м3; v=1,2 см²/с).

Указание. Напор насоса затрачивается на перемещение порш­ня, нагруженного силой F, и на преодоление гидравлических потерь в трубопроводах системы.

35. Определить рабочий напор и подачу насоса объемного гидро­привода, если усилие на штоке силового гидроцилиндра F, ход порш­ня S, число двойных ходов в минуту n, диаметр поршня D ₁, диаметр штока D ₂, механический коэффициент полезного действия гидроци­линдра 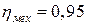, объемный коэффициент полезного действия 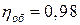. Общая длина трубопроводов системы с учетом эквивалентной длины местных сопротивлений l, диаметр трубопроводов d (рис. 20). Рабочая жидкость в системе — трансформаторное масло ( 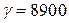Н/м³, v=9,0см²/с).

Указание. Напор насоса затрачивается на перемещение поршня, нагруженного силой F, и на преодоление гидравлических потерь в трубо­проводах системы.

                                            Рис. 20

36. Построить график изменения скорости перемещения поршня силового гидроцилиндра в зависимости от угла 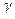 наклона шайбы регу­лируемого аксиально-поршневого насоса (рис. 21). Пределы изменения угла 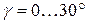. Параметры гидроцилиндра: диаметр поршня D₁, диа­метр штока D₂=0,6. Параметры насоса: z=7, n=800 об/мин, диаметр цилиндров d, диаметр окружности центров цилиндров 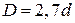. Объемные потери не учитывать.

37. В объемном гидроприводе насос соединен с гидромотором двумя трубами с эквивалентной длиной l и диаметром d (рис. 22). Определить мощность, теряемую в трубопроводе, и перепад давления на гидромо­торе, если полезная мощность насоса N _п, а расход жидкости Q. Рабочая жидкость — трансформаторное масло.

                 Рис. 21                                                    Рис. 22

38. Определить силу F, которую нужно приложить к хвостовику клапана распределительного устройства объемного гидропривода для отрыва его от седла, если усилие затяжки пружины F _пр, давление в по­лости подвода жидкости к клапану р₁, в полости отвода жидкости р₂ (рис. 23). Силы трения покоя и массу клапана не учитывать.

39. Определить силу предварительного натяжения пружины дифференциального предохранительного (переливного) клапана объемного гидропривода, при которой клапан сработает и откроет доступ маслу из системы, как только давление в системе достигнет величины р_с. Диаметры поршней D ₁ и D ₂; диаметр их общего штока d.     

                 Рис. 23                                                 Рис. 24

40. Пользуясь характеристикой гидромуфты, определить расчетный и максимальный моменты, передаваемые ею, а также передаточное отношение, КПД и скольжение при этих режимах, если активный диаметр гидромуфты – D, частота вращения ведущего вала – n ₁, рабочая жидкость – трансформаторное масло. Как изменяются передаваемые крутящий момент и мощность, если частоту вращения ведущего вала увеличить в полтора раза?

Характеристика гидромуфты

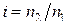
	0	0,2	0,4	0,6	0,8	0,9	1,0
λ·10-7, мин2/м	60	56,5	51	43	32	24	0

41. Пользуясь характеристикой, приведенной в задаче 40, определить активный диаметр и построить внешнюю (моментную) характеристику гидромуфты, предназначенной для работы с асинхронным электродвигателем, развивающим максимальный крутящий момент М_д.макс. при частоте вращения n _д. Рабочая жидкость – минеральное масло.

Указание. Активный диаметр может быть определен по уравнению моментов совмещением режимов гидромуфты при i=0 и электродвигателя при М_д.макс..

42. Пневматический силовой цилиндр нагружен полезной силой F_n. Длина хода поршня - S, избыточное давление в сети - р, масса подвижных частей - m. Определить диаметр пневмоцилиндра, общие усилия на поршень, скорость перемещения поршня, время его перемещения за один двойной ход, число двойных ходов в минуту, объемный расход воздуха и мощность, развиваемую поршнем пневмоцилиндра.

 

Таблица 2. Числовые значения величин
№задачи	Наиме­нование величин и единицы	Предпоследняя цифра шифра
		1	2	3	4	5	6	7	8	9	0
1	Ж	Вода	Керосин	Бензин	Масло трансформаторное	Нефть	Масло турбинное	Глицерин	Спирт	Керосин	Бензин
	р., МПа*	0,02	0,08	0,07	0,08	0,05	0,10	0,02	0,02	0,10	0,05
		(вак.)	(изб.)	(абс.)	(абс.)	(вак.)	(абс.)	(вак.)	(изб.)	(абс.)	(изб.)
	Н, м	5	6	7	8	6	5	5	. 8	7	6
	D,MM	100	200	300	120	140	160	180	200	180	160
	d,MM	50	100	140	60	70	80	90	100	90	80
2	Ж	Нефть	Бензин	Керосин	Вода	Масло трансфарматорное	Глицерин.	Вода	Керосин	Масло турбинное	Бензин
	Н,м	10	20	30	40	30	20	10	50	45	30
	D,MM	300	200	100	300	140	160	180	200	180	160
	d,MM	150	100	50	150	70	90	80	90	10О	90
3	Ж	Масло трансформаторное	Вода	Глицерин	Вода	Масло турбинное	Масло трансформаторное	Вода	Масло турбинное	Вода	Глицерин
	R,H	50	100	150	200	250	200	150	100	50	100
	Н,м	2	1	1.5	2	3	1,5	2	3	1	1,5
	D,мм	500	600	700	600	500	400	350	400	300	200
	d, мм	120	150	180	150	120	100	90	100	75	50
	a,мм	700	700	1000	700	800	500	600	650	500	400
	b,мм	70	80	100	80	70	60	55	55	45	45
4	Ж	Вода	Бензин	Керосин	Вода	Масло трансформаторное	Глицерин	Нефть	Керосин	Масло турбинное	Бензин
	Р., МПа	0,08	0,09	0.07	0,08	0,05	0,09	0,10	0,03	0,10	0,05
		(изб.)	(абс.)	(абс.)	(изб.)	(изб.)	(абс.)	(абс.)	(изб.)	(абс.)	(изб.)
	Рв, МПа	0,01	0,01	0,02	0,02	0,03	0,03	0,01	0,01	0,02	0,02
		(вак.)	(изб.)	(абс.)	(изб.)	(вак.)	(изб.)	(вак.)	(изб.)	(вак.)	(изб.)
	а, мм	200	300	400	100	200	300	200	100	400	200
	h,MM	500	3000	1300	600	500	400	500	300	600	300

 

*Здесь и далее в табл.2 показание пружинного манометра рм, МПа; (вак.) – вакуум; (изб) - избыточное давление; (абс.) – абсолютное давление

 

 

Продолжение таблицы 2.

5	Ж	Бензин	Масло турбинное	Керосин	Вода	Глицерин	Масло трансформаторное	Вода	Керосин	Бензин	Нефть
	H,м	3	4	5	6	5	4	6	5	7	8
	D,мм	500	600	700	600	500	400	500	600	700	400
6	р., МПа	0,5	0,4	0,3	0,8	0,4	0,2	0,6	0,4	0,7	0,6
		(изб.)	(абс.)	(абс.)	(изб.)	(изб.)	(абс.)	(изб.)	(изб.)	(абс.)	(абс.)
	D,мм	1000	1500	2000	2500	2000	1500	1000	1500	2000	2500
	а, мм	700	900	1200	1500	1200	900	700	1000	1300	1500
7	H, м	10	10	7	8	7	9	10	9	8	7
	h, м	4,5	4,5	3	3,5	3	4	4,5	4	3,5	3
	/l,м	46	4,5	3	6	4	4	5,2	6,7	4,65	2
	d, мм	300	30	30	50	40	30	35	50	40	20
8	ж	Вода	Масло трансформаторное	Бензин	Керосин	Глицерин	Вода	Масло	Вода	Бензин	Глицерин
	О.л/с	4	8	0,7	1,5	2,5	10	6	7,5	8	6
	/, м	6	8	10	6	8	10	12	8	6	15
	d., мм	50	70	20	40	40	80	60	70	70	60
9	Ж	Вода	Керосин	Бензин	Масло трансформаторное	Вода	Масло турбинное	Глице­рин	Нефть	Бензин	Керосин
	F, Н	12400	27700	16700	12400	22000	5500	3100	1370	16700	8550
	D, мм	180	270	210	180	240	120	90	60	210	150
	d, мм	60	90	70	60	80	40	30	20	70	50
	/, м	18	27	21	18	24	12	9	6	21	15
10	Ж	Керосин	Бензин	Вода	Глицерин	Масло индустриальное	Вода	Масло трансформаторное	Бензин	Вода	Керосин
	Q,,л/с	0,72	0,21	0,29	251,3	14,4	0,29	8,66	0,21	0,29	0,72
11	Q. м3/с	0,259	0,285	0,306	0,330	0,352	0,376	0.400	0,424	0,447	0,470
	1, см	259	315	366	407	446	179	224	264	300	334
	h" см	30	40	50	60	70	30	40	50	60	70
12	Ж	Керосин	Масло веретен­ное	Вода	Масло веретенное	Керосин	Бензин	Вода	Керосин	Вода	Масло трансформаторное
	d ,мм	20	50	10	60	30	10	8	25	12	80
	l, мм	500	20	400	34	1710	745	203	990	685	225
13	F,H	4· 104	9· 104	7· 104	11· 104·	3· 104	7· 104	20· 104	2, 104	1· 104	2 · 104
	D.MM	200	300	250	300	200	150 .	350	200	200	250
	d,MM	10	15	12	14	16	10	15	12	14	16
	a, мм	45	60	55	50	70	15	20	20	25	30
14	Н,.м	6	5	4	5	6	5	4	8	7	6
	.d, мм	30	50	70	90	70	50	40	60	80	70
15	Н,.м	6	7	8	4	5	6	5	4	5	6
	.d, мм	70	30	50	70	90	70	50	40	60	80
16	Q,,л/с	2,5	3,1	3,8	4,4	5,0	5,6	6,2	7,0	7,5	8,1
	Продолжение таблицы 2
	H,м	3,4	5,2	7,.5	10	13,5	17	21	25	30	35
17	d,мм	15	20	25	30	35	30	25	20	15	20
	D,мм	19	25	31	38	44	37	31	25	18,5	25
	h,CM	35	40	45	50	55	52	42	38	36	40
	Н, см	98	110	125	140	154	145	128	105	100	112
18	и, м/с	2	2,5	3,0	1.5	2,3	2,8	1,6	3,5	3,2	3,0
19	Ж	Бензин	Вода	Масло трансформаторное	Бензин	Глицерин	Керосин	Нефть	Масло трансформаторное	Масло трансформаторное	Вода
	Q,,л/с	0,2	10	0,5	0,3	0,2	0,2	0,2	0,1	0,5	15
	d, мм	16	55	22	16	16	18	16	10	20	70
	l, м	20	1000	50	25	20	25	25	10	50	1500
	б, мм	2	3	2	2	2	3	2	2	2	3
	t зак, с	0,5	2,0	0,7	0,8	0,6	0,7	0,6	0,2	0,6	2,0
20	Q, м3/мин	0,352	1,41	3,18	5,66	8,85	12,7	8,85	5,66	3,18	1,41
	d, мм	50	100	150	200	250	300	250	200	150	100
	1, м	1200	1400	1600	2000	1500	1100	1300 '	1500	1700	1200
	б, мм	7	8,5	9,5	10,5	11,5	12,5	11,5	10,5	9,5	8,5
21	d, мм	100	150	200	250	300	250	200	150	100	50
	1, м	1900	1700	1850	1750	1450	1900	1600	1800	1500	2000
	б, мм	7	8	8	10	12	11	10	9	8	6
22	Q. л/с	15	25	35	62	30	22	14	100	53	32
	d., мм	100	125	150	200	150	125	100	250	200	150
	/.м	15	18	12	15	14	13	17	16	20	15
	n,об/мин	2860	2850	2740	1470	2500	2890	1475	1450	1500	2000
	С	1000	1100	1200	800	1000	900	1200	800	900	1000
23	Q. л/с	15	25	36	63	36	25	15	25	36	15
	H, м	10	8	9	20	15	12	10	5	8	16
	d, мм	100	125	150	200	150	125	100	125	150	100
	/V,, кВт	2,3	3,2	5,0	17,3	7,7	4,4	2,3	2,3	4,6	3,4
	n,об/мин	3000	2500	2000	1500	3000	3000	2000	2800	3000	2700
24	р„МПа	0,17	0,075	0,18	0,18	0,08	0,02	0,02	0,025	0,03	0,09
		(абс.)	(изб.)	(абс.)	(абс.)	(изб.)	(вак.)	(изб.)	(вак.)	(вак.)	(абс.)
	/, м	90	1.12	225	180	135	113	90	225	180	135
	d, мм	100	125	250	200	150	125	100	250	200	150
	h, м	2,0	2,5	3,0	3,5	4,0	1.0	5,0	0,5	0	2,0
	Q, л/с	15	25	98	63	36	24	14	100	62	35
25	H„м	30	45	6	30	30	60	60	6	15	15
	d, мм	200	100	250	100	50	80	100	200	70	300
	/, м	6	25	40	15	60	7	36	8	12	280
	Qо, мэ/с	0,7	0,1	0,3	0,1	0,01	0,1	0,1	0,3	0,03	0,3
	Но, м	100	150	20	100	100	200	200	20	50	50
26	Нr, м	24	30	^^^=*г- 45	40	60	30	25	40	50	60
	d, мм	180	185	180	180	200	170	130	170	190	250
	/, м	185	190	185	190	210	175	125	175	200	260
	Qо, мэ/с	0.05	0.06	0,07	0,065	0,10	0,05	0,025	0,06	0,08	0,15
	Но, м	80	100	150	130	200	100	80	140	160	200
27	Нr, м	60	24	30	45	40	60	30	25	40	50
	d, мм	260	187	195	190	190	210	180	135	180	200
	Qо, мэ/с	0,15	0,05	0,06	0,07	0,065	0,10	0,05	0,025	0,06	0,08
	Но, м	200	80	100	150	130	200	100	80	140	160
28	D, мм	200	300	250	100	200	300	160	250	300	280
	Продолжение таблицы 2
	S, мм	150	250	200	60	250	300	100	250	350	250
	d, мм	50	75	62,5	25	50	75	40	62,5	75	70
	n, об/мин	50	60	70	60	80	60	50	' 75	60	90
	W, мэ	0,52.	1,45	1,13	0,077	0,86	3,5	0,2	1,76	3,7	3,0
	t, с	80	50	60	100	50	100	80	70	90	80
29	Q, л/с	30	50	65	150	200	150	100	60	120	200
	Hr, м	10	15	20	15	10	25	20	30	35	25
	l, м	20	25	30	35	40	35	30	25	20	40
	d, мм	100	150	200	250	300	250	200	150	250	300
	n, об/мин	100	90	80	70	60.	90	80	70	60	100
30	D,мм	80	90	100	110	120	70	90	100	110	80
	S,мм	200	260	160	220	180	240	280	300	320	340
	n, ход/мин	60	75	50	65-	55	70	80	85	90	95
	dн, мм	64	72	80	88	96	56	72	80	88	64
	b, мм	50	65	40	55	45	60	70	75	80	85
31	F,  Н	90 000	80 000	70 000	60 000	50 000	60 000	70 000	80 000	90 000	100 000
	S, см	100	115	120	100	110	105	120	130	105	112
	n , об	12	10	20	11	10	20	25	20	10	15
	D, мм	145	150	130	120	110	120	130	140	145	155
	d, мм	50	50	45	40	40	40	45	45	50	'52
32	F1,H.	5500	8250	11000	13750	16500	4130	6900	9600	12400	15 100
	Q, л/с	6	9	12	15	18	4,5	7,5	10,5	13,5	16,5
33	F1,H	7000	9500	12000	10 500	12400	20 700	20 500	20 700	28100	30700
	F2, Н	3230	1350	5250	2140	2 000	8000	5400	3000	8000	7000
	Q, л/с	12	14	16	18	20	22	24	2б	28	30
34	F,Н	50 000	60 000	70 000	80000	90 000	100 000	90000	80000	70 000	6О000
	v, см/c	4	9,5	12,5	8,6	3,5	5,6	3,4	11	8	5,3
	D1, мм	110	120	130	138	145	155	145	138	130	120
	D2, мм	3б	40	44	46	48	52	48	4б	43	40
	1, м	10	15	12	10	8	14	12	10	8	12
	d,мм	15	20	25	22	14	20	15	25	20	15
35	F,Н	60000	70 000	80000	90 000	100 000	90 000	80000	70000	60 000	50000
	S,мм	150	120	220	100	112	105	130	150	145	120
	п,об/мин	lО,6	20	10	10	15	10	20	25	20	10
	D1, мм	120	130	138	145	155	145	138	130	120	110
	D2, мм	40	43	4б	48	52	48	46	44	40	36
	l,, м	25	20	22	25	18	16	20	24	30	20
	d, мм	15	20	25	15	20	14	22	25	20	15
36	D1,мм	95	135	175	225	275	112	210	255	325	235
	d,мм	20	25	30	35	40	22	34	38	45	36
37	N1,кВт	5	6	7,5	10	12	14	5	10	8	10
	Q,л/с	0,5	0,62	0,75	0,98	1,24	1,4	0,5	1,0	0,76	1,06
	l,м	36	40	44	50	56	60	36	50	44	52
	d,мм	18	20	22	250	28	30	18	25	22	26
38	Fпр,Н	300	350	400	250	420	320	300	350	400	450
	p1,МПа	0,6	0,7	0,8	0,5	0,85	0,65	0,6	0,7	&0	0,85
	p2,МПа	0,4	0,5	0,6	0,3	0,55	0,35	0,3	0,4	0,6	0,65
	D1,мм	50	55	45	40	50	56	48	50	55	45
	D2,мм	40	45	35	30	40	45	з8	42	45	35
	d,мм	10	12	11	10	12	11	12	10	12	11
39	pc,МПа	0,255	0,315	0,4	0,52	0,71	0,52	0,4	0,315	0,255	1,0
	D1,мм	100	90	80	70	6О	70	80	90	100	50
	Продолжение таблицы 2
	D2,мм	50	45	40	35	30	35	40	·45	50	25
	d,мм	25	20	20	18	10	lб	15	20	25	12
40	D,см	440	420	500	450	440	430	420	460	480	500
	n1,об/мин	1500	2000	1500	1200	2200	1800	1400	1000	1300	lБОО
41	Mд.макс, H*m	300	350	250	400	300	350	250	400	270	280
	nд,об/мин	2200	1100	1100	2200	1100	2200	2200	2200	1100	2200
42	Fn,Н	14500	1500	1400	14800	16000	17000	17500	15200	18 000	15800
	S,мм	200	220	240	250	300	180	300	280	240	200
	Pизб,МПа	0,45	0.45	0,5	0,45	0,55	0,4	0,6	0,58	0,45	0,5
	m,кг	80 ·10000	85·10000	75·10000	78·10000	90·10000	70·10000	74·10000	85·10000	70·10000	82·10000

 

 

 

ПРИЛОЖЕНИЕ

 

1. Удельный вес y и плотность p жидкостей при t =20 C
Наименование	y, Н/м2	p,кг/м3
Бензин авиационный	7250 .. 7350	739…751
Вода пресная	9790	998,2
Глицерин безводный	12260	1250
Керосин	7770…8450	792…840
Масло касторовое	9250	970
Масло минеральное	8600..8750	877…892
Нефть	8340…9320	850…950
Ртуть	132900	13547
Спирт этиловый безводный	7740	789,3
Масло трансформаторное	8870…8960	904…915
Масло турбинное	9200…9300	940…952

 

 

2. Кинематический коэффициент вязкости жидкостей v при t =20С
Жидкость	V,см2/с	Жидкость	v, см2/с
Бензин авиационный	0,0073	Глицерин	8,7
Керосин Т-1	0,025	Воздух	0,149
Вода	0,010	Масло трансформаторное	0,3
Ртуть	0,0016	Масло индустриальное	0,5

 

 

Дата: 2019-03-05, просмотров: 287.

Механика жидкости и газа     МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ   для студентов-заочников инженерно-технических специальностей высших учебных заведений     ИЗДАНИЕ ЧЕТВЁРТОЕ   Москва «Высшая школа» 1990 УДК 621.226 Гидравлика: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений /И.А. Гилинский. – 4-е изд.– М.: Высш.шк. ,1990. – 62 с.: ил. Общие методические указания   В первой части курса — гидравлика — изучаются законы равно­весия и движения жидкости, рассматриваются способы применения этих законов к решению практических инженерных задач. Во второй и третьей частях — лопастные гидромашины и гидродинамические передачи, объемные насосы и гидравлические приводы — изучаются устройство и принцип действия, теория и элементы расчета насосов, гидравлических приводов и передач, в которых жидкость служит носи­телем механической энергии. При изучении материала по учебнику, студент должен особое внимание обратить на проработку основных положений темы (раздела), используя для этой цели методические указания, основное предназна­чение которых — облегчить студенту работу с книгой. Методические указания к каждой теме (разделу) заканчиваются вопросами для самопроверки, охватывающими наиболее существенные положения учебного материала. Курс целесообразно изучать последовательно по темам (разделам), руководствуясь программой и методическими указаниями. Сначала следует изучить теоретическую часть раздела, затем решить и проана­лизировать приведенные в учебнике и задачниках примеры и задачи с решениями. После этого необходимо ответить на вопросы для самопроверки. Учебный материал можно считать проработанным и усво­енным только при условии, если студент умеет правильно применить теорию для решения практических задач. Существенное значение имеет правильный выбор учебника. Не следует одновременно пользоваться несколькими учебниками. Один из учебников, рекомендуемый в списке учебной литературы, должен быть принят в качестве основного. Другие учебники и учебные пособия используют в том случае, если прорабатываемый раздел отсутствует или недостаточно подробно изложен в основном учебнике.                                               ЛИТЕРАТУРА                                                          Основная 1. Гидравлика, гидравлические машины и гидравлические приводы/Башта Т. М., Руднев С. С., Некрасов Б. Б. и др. М., 1982. 2. Некрасов Б. Б. Гидравлика и ее применение на летательных аппаратах. М., 1967. 3. Гидравлика и гидропривод/Гейер В.Т., Дулин В.С., Боруменский А.Г., Заря А.Н. М., 1970. 4. Осипов П.Е. Гидравлика и гидравлические машины. М., 1965. 5. Сборник задач по машиностроительной гидравлике/Под ред. И.И. Куколевского и Л.Г. Подвидза. М., 1981. 6. Лабораторный курс гидравлики, насосов и гидропередач/Под ред. С.С. Руднева и Л.Г. Подвидза. М., 1974. Дополнительная 7. Башта Т.М. Машиностроительная гидравлика: Справочное пособие. М., 1971. 8. Ковань П.В. Гидропривод горных машин. М., 1967. 9. Ибатулов К.А. Гидравлические машины и механизмы в нефтянности. М., 1972.                                     МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ТЕМАМ И РАЗДЕЛАМ КУРСА ЧАСТЬ I. ГИДРАВЛИКА   Основные свойства жидкости Определение жидкости. Силы, действующие на жидкость. Давление в жидкости. Сжимаемость. Закон Ньютона для жидкостного трения. Вязкость. Поверхностное натяжение. Давление насыщенного пара жидкости. Растворение газов в жидкости. Модель идеальной жидкости. Неньютоновские жидкости. Методические указания По своим физическим свойствам жидкости занимают промежуточ­ное положение между твердыми телами и газами. Жидкость мало изменяет свой объем при изменении давления или температуры, в этом отношении она сходна с твердым телом. Жидкость обладает текучестью, благодаря чему она не имеет собственной формы и принимает форму того сосуда, в котором находится. В этом отношении жидкость отличается от твердого тела и имеет сходство с газом. Свойства жидкостей и их отличие от твердых тел и газов обуславливаются молекулярным строением. Следует уяснить, каким образом особенности молекулярного строения влияют на физические свойства жидкости. Покоящаяся жидкость подвержена действию двух категорий внешних сил: массовых и поверхностных. Массовые силы пропорциональны массе жидкости или для однородных жидкостей – ее объему. Внешние поверхностные силы непрерывно распределены по граничной поверх­ности жидкости. Следует знать, какие силы относятся к массовым (объемным) и к поверхностным силам, какие силы называются внеш­ними и какие внутренними. В покоящейся жидкости может существовать только напряжение сжатия, т. е. давление. Необходимо чётко представлять разницу между понятиями среднего гидростатического давления, гидростатического давления в точке, выраженных в единицах напряжения, и понятием суммарного гидростатического давления на поверхность, выраженного в единицах силы. В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (на­пример, плотность). Студенту нужно уметь определять основные физи­ческие характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капель­ных жидкостей: сжимаемость, тепловое расширение, вязкость и др. Вязкостью называется свойство жидкости оказывать сопротивление относительному перемещению слоев, вызывающему деформацию сдвига. Это свойство проявляется в том, что в жидкости при ее движении возникает сила сопротивления сдвигу, называемая силой внутреннего трения. При прямолинейном слоистом движении жидкости сила внут­реннего трения Т между перемещающимися один относительно другого слоями с площадью соприкосновения S определяется законом Ньютона:                                или .                      (1)                                                            Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свой­ствами жидкости и ее температурой. Как видно из (1), сила Т и каса­тельное напряжение  пропорциональны градиенту скорости u и по нор­мали n к поверхности трения , который представляет собой изменение скорости жидкости в направлений нормали на единицу длины нормали. Жидкости, для которых зависимость изменения каса­тельных напряжений от скорости деформации отличается от закона Ньютона (1), называются неньютоновскими или аномальными жид­костями. Учет сил вязкости значительно осложняет изучение законов дви­жения жидкости. С другой стороны, капельные жидкости незначи­тельно изменяют свой объем при изменении давления и температуры. В целях упрощения постановки задач и их математического решения создана модель идеальной жидкости. Идеальной жидкостью называется воображаемая жидкость, которая характеризуется полным отсутствием вязкости и абсолютной неизменяемостью объема при изменении давления и температуры. Переход от идеальной жидкости к реальной осуществляется введением в конечные расчетные формулы поправок, учитывающих влияние сил вязкости и полученных, главным образом, опытным путем. При изучении гидродинамики следует проследить осо­бенности перехода от идеальной жидкости к реальной. В гидравлике жидкость рассматривается как сплошная среда (континуум), т.е. среда, масса которой распределена по объему непрерывно. Это позволяет рассматривать все характеристики жид­кости (плотность, вязкость, давление, скорость и др.) как функции координат точки и времени, причем в большинстве случаев эти функции предполагаются непрерывными. Литература: [1, с. 8—15]; [2, с: 9—18]; [3, с. 9—17]; [14, с. 9—14]; [6, с. 4—12]; [8, с. 5-10].   Вопросы для самопроверки 1. В чем отличие жидкостей от твердых тел и газов? 2. Какова взаимосвязь между плотностью и удельным весом жидкости? Укажите их единицы. 3. Что называется коэффициентом объемного сжатия жид­кости? Какова его связь с модулем упругости? 4. Что называется вязкостью жидкости. В чем состоит закон вязкого трения Ньютона? 5. В чем принципиальная разница между силами внутреннего трения в жидкости и силами трения при относительном перемещении твердых тел? 6. Какова связь между динамическим и кинематическим коэффи­циентами вязкости? Укажите их единицы. 7. Укажите свойства идеаль­ной жидкости. С какой целью в гидравлике введено понятие об идеаль­ной жидкости? В каких случаях при практических расчетах жидкость можно считать идеальной?   Гидростатика Свойства давления неподвижной жидкости. Уравнение Эйлера равновесия жидкости. Интегрирование уравнения Эйлера. Поверхности равного давления. Свободная поверхность жидкости. Основное уравнение гидростатики. Закон Паскаля. Приборы для измерения давления. Сила давления жидкости на плоские и криволинейные стенки. Закон Архимеда. Плавание тел. Относительный покой жидкости. Методические указания Два свойства гидростатического давления обусловлены тем, что покоящаяся жидкость не воспринимает касательных и усилий. Знание этих свойств позволяет понять форму статического силового воздействия жидкости. Наиболее общими уравнениями гидростатики являются дифференциальные уравнения Эйлера, устанавливающие и поверхностными силами, действующими в жидкости. При изучении этих уравнений следует усвоить физический смысл всех входящих в них величин. Эти уравнения позволяют просто и быстро решать задачи как в случае абсолютного покоя жидкости, когда на жидкость из массовых сил действует только сила тяжести, так и в случае относительного покоя, когда к силе тяжести присоединяются силы инерции. В случае действия на жидкость одной лишь силы тяжести интегрирование урав­нений Эйлера дает основное уравнение гидростатики                                                 р2=р1+ γh ,                                                     (2) где р1 и р2 —давления в точках 1 и 2; h — глубина погружения точки 2 относительно точки 1; — удельный вес жидкости; h — весо­вое давление столба жидкости глубиной h. В зависимости от способа отсчета различают абсолютное, избыточ­ное (манометрическое) и вакуумметрическое давление. Следует знать взаимосвязь этих величин. В уравнении (2) точка 1 может лежать на свободной поверхности жидкости. При этом весовое давление h будет избыточным давлением только в том случае, когда давление на свободную поверхность равно атмосферному давлению. Весьма важными понятиями в гидравлике являются пьезометрическая высота и гидростатический напор. Пьезометрическая высота выражает в метрах столба жидкости избыточное (или абсолютное) давление в рассматриваемой точке жидкости. Гидростатический напор равен сумме геометрической z и пьезометрической р/γ высот. Для всех точек данного объема покоящейся жидкости гидростатический напор относительно выбранной плоскости сравнения есть постоянная величина. Воздействие жидкости на плоские и криволинейные поверхности наглядно отражается эпюрами давления. Площадь (объем) эпюры дает величину силы давления, а центр тяжести этой площади (объема) — точку приложения силы давления. Аналитическое рассмотрение задачи позволяет получить весьма простые расчетные формулы. В случае плоской поверхности любой формы величина силы гидростатического давления равна смоченной площади этой поверхности, умноженной на гидростатическое давление в центре тяжести площади. Точка приложения силы гидростатического давления (центр давления) лежит всегда ниже центра тяжести (за исключением давления на горизонтальную плоскость, когда они совпадают). Следует указать, что формула для определения координаты центра давления дает точку приложения силы только гидростатического давления без учета давления на свободную поверхность (см. вывод формулы в любом учебнике гидравлики).  Для криволинейных цилиндрических поверхностей обычно опреде­ляют горизонтальную и вертикальную составляющие полной силы гидростатического давления. Определение вертикальной составляющей связано с понятием «тела давления», которое представляет собой действительный или воображаемый объем жидкости, расположенный над цилиндрической поверхностью. Линия действия горизонтальной составляющей проходит через центр давления вертикальной проекции криволинейной поверхности, а линия действия вертикальной состав­ляющей — через центр тяжести тела давления. При изучении этого раздела студенту полезно рассмотреть несколь­ко конкретных примеров построения тел давления для цилиндриче­ских поверхностей, определить самостоятельно вертикальную и гори­зонтальную составляющие силы давления, точки их приложения результирующую силу. Необходимо рассмотреть давление жидкости на стенки труб и резервуаров н расчетные формулы для определения толщины их стенок. Литература: [1, с. 16—39]; [2, с. 19—47]; [3, с, 17—34]; [4, с. 15—60]; [5, с. 7—103]; [6 с. 12—16]; [8, с. 10—22]   Вопросы для самопроверки 1. Каковы свойства гидростатического давления? 2. Объясните физический смысл величин, входящих в дифференциальные уравнения равновесия жидкости Эйлера. 3. Что такое поверхность равного давле­ния и каковы ее форма и уравнение при абсолютном покое жидкости, в случае движения сосуда по горизонтальной плоскости с ускорением, при вращении сосуда вокруг вертикальной оси? 4. Как формулируется закон Паскаля и какова его связь с основным уравнением гидроста­тики? 5. Приведите примеры гидравлических установок, действие кото­рых основано на законе Паскаля. 6. Каковы соотношения между абсо­лютным давлением, избыточным и вакуумом? Что больше: абсолютное давление, равное 0,12 МПа, или избыточное, равное 0,06 МПа? 7. Чему равна пьезометрическая высота (в метрах водяного столба) для атмо­сферного давления? 8. Почему центр давления всегда находится ниже центра тяжести смоченной поверхности наклонной плоской стен­ки? 9. Сформулируйте закон Архимеда. В каких случаях положение судна будет остойчивым и неостойчивым? Кинематика и динамика жидкости Виды движения жидкости. Основные понятия кинематики жид­кости: линия тока, трубка тока, струйка, нормальное сечение, расход. Поток жидкости. Средняя скорость. Уравнение расхода. Дифферен­циальные уравнения движения идеальной жидкости. Уравнение Бернулли для установившегося движения идеальной жидкости. Геометрическое и энергетическое толкование уравнения Бернулли. Уравнение Бернулли для потока вязкой жидкости. Коэффициент Кориолиса. Общие сведения о гидравлических потерях. Виды гидравлических потерь. Трубка Пито, водомер Вентури. Методические указания Одним из основных уравнений гидродинамики является уравнение постоянства расхода (уравнение неразрывности), которое для плавно изменяющегося и параллельностройного движения может быть пред­ставлено в виде v·S= const (вдоль потока), откуда для двух сечений 1 и 2 получим v1/v2= S 2 / S 1, т.е. средние скорости потока обратно пропорциональны площадям живых сечений. Следует уяснить, что уравнение постоянства расхода справедливо только при соблюдении ряда допущений, на которых основан логиче­ский вывод этого уравнения. Дифференциальные уравнения движения идеальной жидкости Эй­лера дают общую зависимость между скоростями и ускорениями движущихся частиц жидкости и силами, действующими на эти частицы. Интегрирование этих уравнений для элементарной струйки идеальной жидкости приводит к основному уравнению гидродинамики — уравне­нию Бернулли, которое можно получить также и непосредственно, при­менив к бесконечно малому объему жидкости теоремы механики, например теорему живых сил. Уравнение Бернулли представляет собой частный случай закона сохранения энергии. Все члены уравнения Бернулли отнесены к единице веса жидкости, поэтому все виды энергии в этом уравнении имеют линейную размерность. При рассмотрении уравнения Бернулли для простейшего случая движения элементарной струйки невязкой (идеаль­ной) жидкости следует уяснить геометрический и физический (энер­гетический) смысл уравнения в целом и его отдельных членов, а также обратить внимание на условия применимости уравнения Бернулли к элементарной струйке. При распространении уравнения Бернулли для элементарной струй­ки на поток реальной жидкости возникает ряд трудностей, которые пре­одолеваются введением соответствующих ограничений и поправок. Уравнение Бернулли составляется для двух живых сечений потока, в которых течение параллельностройное или плавно изменяющееся. Живые сечения здесь плоские, поэтому отсутствуют ускорения вдоль живых сечений, а из массовых сил действует только сила тяжести. Следовательно, в этих сечениях (участках) справедливы законы гид­ростатики, в частности постоянство гидростатического напора для всех точек живого сечения относительно любой плоскости сравнения. Между плавно изменяющимися течениями (участками) потока, связанными уравнением Бернулли, поток может быть и резко изменяющимся. При определении кинетической энергии потока по средней скорости в данном сечении вводится поправка в виде коэффициента Кориолиса α, учи­тывающего неравномерность распределения скоростей по живому се­чению. При решении практических инженерных задач уравнение Бернулли и уравнение постоянства расхода используются совместно. При этом они составляют систему из двух уравнений, позволяющую решать задачи с двумя неизвестными. Если для струйки идеальной жидкости уравнение Бернулли пред­ставляет собой закон сохранения механической энергии, то для потока реальной жидкости дно является уравнением баланса энергии с учетом гидравлических потерь. Гидравлическими потерями называется работа сил трения, затраченная на перемещение единицы веса жидкости из одного сечения в другое. Энергия потока, израсходованная на работу сил трения, превращается в тепловую энергию и рассеивается в про­странстве. Литература: [1, с. 40—61]; [2, с. 48—72]; [3. с. 37—57]; [4, с. 61—87]; [6, с. 16—21]; [8, с. 23—32].   Вопросы для самопроверки 1. Дайте определение и приведите примеры основных видов дви­жения жидкости: установившегося и неустановившегося, напорного и безнапорного, равномерного и неравномерного, медленно изменяю­щегося. 2. Что такое линия тока, трубка тока и элементарная струйка? 3. При каких условиях сохраняется постоянство расхода вдоль потока? 4. Укажите физический смысл величин, входящих в дифференциальные уравнения гидродинамики Эйлера. 5. Объясните геометрический и физи­ческий смысл понятий: геодезический, пьезометрический и гидравли­ческий уклоны. Может ли быть отрицательным гидравлический уклон? пьезометрический уклон? 6. Когда линия полной энергии и пьезометри­ческая линия параллельны? Когда в направлении движения жидкости эти линии сближаются и когда удаляются одна от другой? 7. Какие существуют ограничения в применении уравнения Бернулли? 8. К каким выражениям приводится уравнение Бернулли в случаях: а) неподвиж­ной жидкости; б) равномерного движения в горизонтальном трубо­проводе; в) истечения жидкости из сосуда через круглое небольшое отверстие. 9. Каковы причины возникновения потерь напора при движении вязкой жидкости? Дайте определение понятию «гидравличе­ские потери напора».