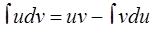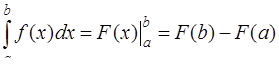
| 1. | 
| 8. |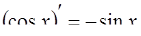 
|
| 2. |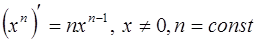 
| 9. |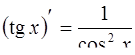 
|
| 3. |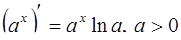 
| 10. |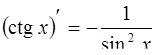 
|
| 4. |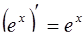 
| 11. | 
|
| 5. |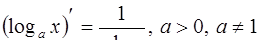 
| 12. |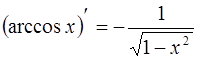 
|
| 6. |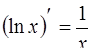 
| 13. |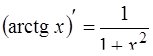 
|
| 7. |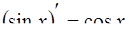 
| 14. |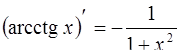 
|
Здесь 
.
Приложение 5
ТАБЛИЦА интегралов
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
| 1. |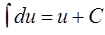 
| 10. |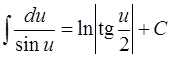 
|
| 2. |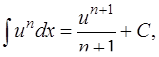  
| 11. |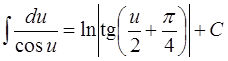 
|
| 3. |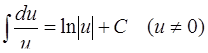 
| 12. |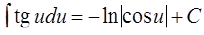 
|
| 4. |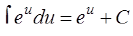 
| 13. |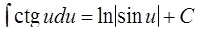 
|
| 5. |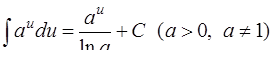 
| 14. |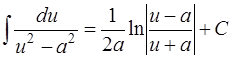 
|
| 6. |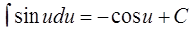 
| 15. |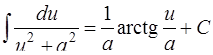 
|
| 7. |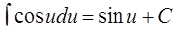 
| 16. |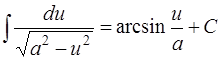 
|
| 8. |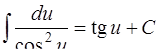 
| 17. |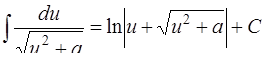 
|
| 9. |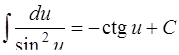 
| ||
| Формула интегрирования по частям: Формула Ньютона–Лейбница: | |||
Некоторые тригонометрические формулы
; 
; 
;
;
;
.
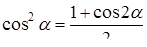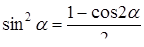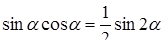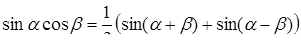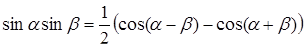Ряды
Необходимый признак сходимости ряда: Если ряд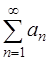 
сходится, то 
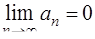(если же 
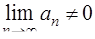, то ряд расходится).
Радикальный признак Коши: Если для положительного ряда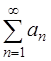 
существует предел 
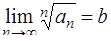, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b = 1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Признак Даламбера: Если для положительного ряда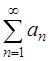 
существует предел 
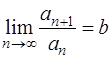, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b = 1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Предельный признак сравнения: Если существует конечный и отличный от нуля предел 
то положительные ряды 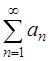и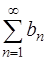 
одинаковы в смысле сходимости.
Обобщенный гармонический ряд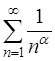 
1) сходится при 
;
2) расходится при ( здесь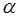 
– действительное число).
Признак Лейбница для знакочередующихся рядов: Ряд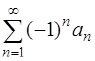 
сходится, если выполняются два условия:
1) 
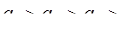; 2)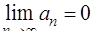 
.
Радиус сходимости R степенного ряда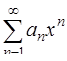 
, 
.
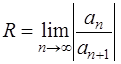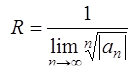Дифференциальные уравнения
Линейное дифференциальное уравнение первого порядка
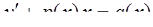
решается методом Бернулли с помощью подстановки
, 
.
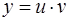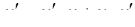Однородное дифференциальное уравнение первого порядка
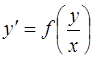
решается с помощью замены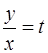 
, 
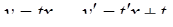
При решении однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами
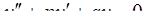
составляется характеристическое уравнение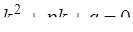 
.
При этом общее решение имеет вид
1) 
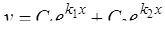, если корни k1 и k2 действительны и различны (дискриминант D > 0, 
);
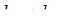2) 
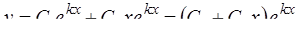, если корни k1 и k2 действительные и равные (D = 0, k1 = k2);
3) 
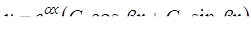, если корни k1 и k2 комплексные (D < 0, 
).
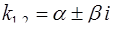Приложение 6
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
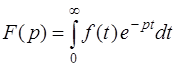(или коротко: 
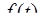l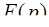 
,
где 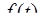– функция-оригинал, 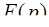– ее изображение)
ТАБЛИЦА ОРИГИНАЛОВ И ИХ ИЗОБРАЖЕНИЙ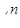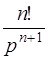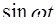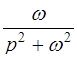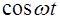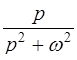
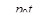 l  ,
|  l  ,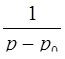
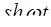|  l  ,
|
 l  ,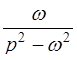
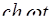|  l  ,
|  l  .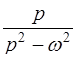
|
Замечание. На самом деле здесь перечислены изображения элементарных функций, умноженных на единичную функцию Хевисайда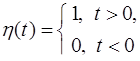 
, которую обычно не пишут. Сама же функция Хевисайда имеет изображение 
.
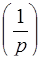Теорема Бореля: f ( t )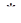 
g ( t ) l F ( p ) ·G ( p )
Дифференцирование оригинала:
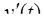 l  ,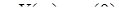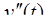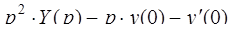
|
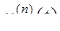 l 
|
| … |
 l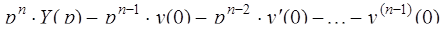 
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособ. для втузов. – СПб: «Специальная Литература», 1998. 446 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2004. 404 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2004. 479 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособ. для втузов: В 2 ч. Ч. Ι. 5–е изд., испр. – М.: Высш. шк., 1998. 304 с.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособ. для втузов: В 2 ч. Ч. ΙΙ. 5–е изд., испр. – М.: Высш. шк., 1998. 416 с.
6. Евдокимов М.А., Лиманова Л.В. Интегральное исчисление и его приложения: Учебник – Самара: Самар. гос. техн. ун-т, 2008. – 168 с.
7. Задачи и упражнения по математическому анализу. Под ред. Б. Демидовича. М.: Интеграл-пресс,1997.416 с.
8. Квальвассер В.И., Фридман М.И. Теория поля. Теория функций комплексного переменного. Операционное исчисление. М.: Высшая школа, 1967. 240 с.
9. Краснов М.И., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981. 256 с.
10. Кручкович Г.И., Мордасова Г.М. Сборник задач и упражнений по специальным главам высшей математики. М.: Высшая школа, 1970. 511 с.
11. Кузнецов В.А., Самарин Ю.П. Математика-8 для студентов вузов. Теория вероятностей: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2001.131 с.
12. Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного переменного. М.: Лань, 2002. 688 с.
13. Мартыненко В.С. Операционное исчисление. Киев: Высшая школа, 1990. 359 с.
14. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1. – М.: Интеграл–ПРЕСС, 2004.
15. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.2. – М.: Интеграл–ПРЕСС, 2002.
16. Самарин Ю.П., Сахабиева Г.А. Математика-2 для студентов вузов. Линейная алгебра и аналитическая геометрия: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2000. 96 с.
17. Самарин Ю.П., Сахабиева Г.А. Математика-3 для студентов вузов. Введение в математический анализ: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2000. 45 с.
18. Самарин Ю.П., Сахабиева Г.А. Математика-4 для студентов вузов. Дифференциальное исчисление: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2000. 84 с.
19. Самарин Ю.П., Сахабиева Г.А. Математика-5 для студентов вузов. Интегральное исчисление для функции одной переменной: Учеб. пособ. - Самара: Самар. гос. техн. ун-т, 2000. 54 с.
20. Самарин Ю.П., Сахабиева Г.А. Математика-6 для студентов вузов. Кратные, криволинейные и поверхностные интегралы; элементы теории поля: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2000. 61 с.
21. Самарин Ю.П., Сахабиева Г.А. Математика-7 для студентов вузов. Ряды: Учеб. пособ. – Самара: Самар. гос. техн. ун-т, 2000. 72 с.
22. Сборник задач по математике. Болгов В.А., Демидович Б.П., Ефимов А.В. и др.; М.: Наука, 1993. 480 с.
23. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. М.: Физматлит: Лаб.знаний.Т.1.2003.679 с.
ОГЛАВЛЕНИЕ
ГЛАВА 1
Дата: 2019-03-05, просмотров: 213.
