Операционное исчисление,
Теория вероятностей
Теория функций комплексной переменной
Рассматриваются следующие задачи: действия с комплексными числами; решение уравнений с комплексной переменной; интегрирование функции комплексной переменной.
Задача 77. Представить в тригонометрической и показательной форме число 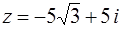 .
.
Решение. Число задано в алгебраической форме и в общем случае имеет вид
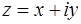 .
.
Здесь х и у – соответственно действительная и мнимая части комплексного числа z, а i – мнимая единица (i2 = −1).
Число z изображается на комплексной плоскости точкой с координатами х и у (рис. 7).

Рис.7
Алгебраическая, тригонометрическая и показательная формы связаны соотношениями
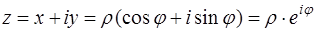 ,
,
где 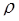 – модуль комплексного числа z (радиус-вектор, соединяющий начало координат с точкой z);
– модуль комплексного числа z (радиус-вектор, соединяющий начало координат с точкой z); 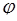 – аргумент комплексного числа z (угол между осью Ох и радиус-вектором
– аргумент комплексного числа z (угол между осью Ох и радиус-вектором 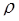 ).
).
При этом
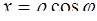 ,
, 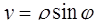 .
.
С другой стороны,
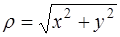 ,
, 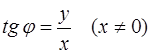 .
.
В силу многозначности 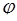 будем рассматривать только его главное значение из промежутка
будем рассматривать только его главное значение из промежутка 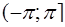 , используя соотношение
, используя соотношение
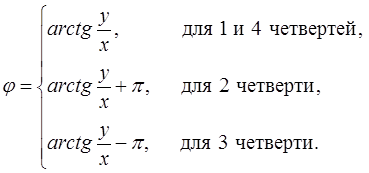 .
.
Для 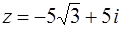 имеем
имеем
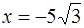 ,
, 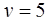 ,
,
поэтому
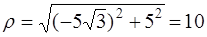 .
.
Так как
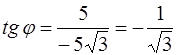
и число z расположено во второй четверти (рис. 8), получим
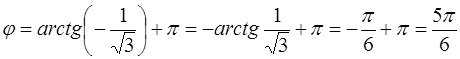 .
.
Тогда
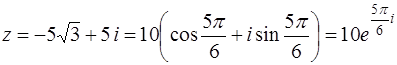 .
.

Рис. 8
Задача 78. Представить в тригонометрической и показательной форме число 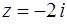 .
.
Решение. Здесь х = 0, у = −2 (см. задачу 77), поэтому 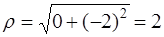 . Построив
. Построив 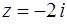 (рис. 9), определим
(рис. 9), определим 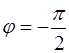 (формула
(формула 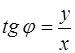 неприменима, так как х = 0).
неприменима, так как х = 0).
Рис. 9
Итак,
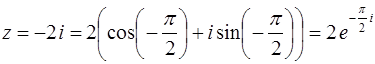 .
.
Задача 79. Вычислить 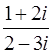 .
.
Решение. Выполнить действия с комплексными числами − значит представить результат в алгебраической, тригонометрической или показательной формах (см. задачу 77). В данном случае получим алгебраическую форму вида 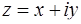 , для чего умножим числитель и знаменатель дроби на комплексно сопряженное к знаменателю число (
, для чего умножим числитель и знаменатель дроби на комплексно сопряженное к знаменателю число ( 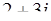 ). В результате получим
). В результате получим
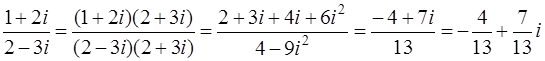 .
.
Задача 80. Вычислить 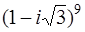 .
.
Решение. Возвести комплексное z число в степень n можно по формуле Муавра
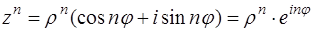 ,
,
где 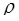 и
и 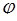 − соответственно модуль и аргумент комплексного числа z.
− соответственно модуль и аргумент комплексного числа z.
Найдем 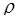 и
и 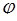 (см. задачу 77). Так как х = 1,
(см. задачу 77). Так как х = 1, 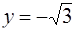 , получим
, получим
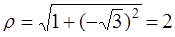 .
.
Поскольку число z расположено в четвертой четверти (рис. 10), имеем
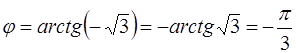 .
.

Рис. 10
Тогда
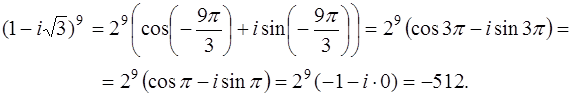
Задача 81. Решить уравнение 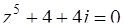 .
.
Решение. Преобразуем уравнение к виду
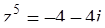 .
.
Тогда
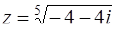
и, значит, следует применить формулу Муавра извлечения корня степени n из комплексного числа
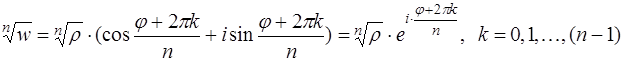 .
.
Здесь 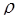 и
и 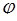 − соответственно модуль и аргумент подкоренного выражения z.
− соответственно модуль и аргумент подкоренного выражения z.
Находим 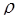 и
и 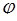 для числа
для числа 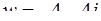 (см. задачу 77):
(см. задачу 77):
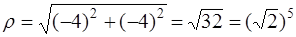 .
.
Так как число w расположено в третьей четверти (рис. 11), то
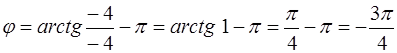 .
.
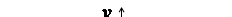
Рис. 11
Далее получаем
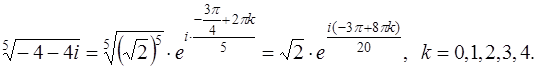
Задача 82. Вычислить 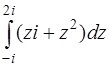 .
.
Решение. Поскольку i − число ( 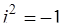 ), а
), а
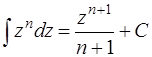 ,
,
имеем
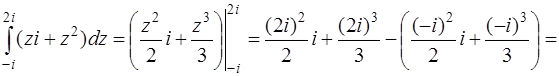
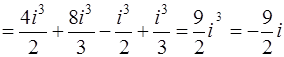 .
.
Операционное исчисление
Рассматриваются задачи: нахождение изображения по заданному оригиналу; нахождение оригинала по заданному изображению, нахождение изображения свертки с применением теоремы Бореля; решение дифференциальных уравнений операционным методом.
Задача 83. Найти изображение F ( p ) для функции-оригинала
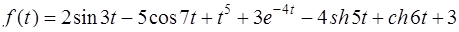 .
.
Решение. Функция-оригинал f ( t ) и ее изображение F ( p ) связаны соотношением
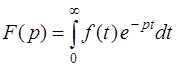 (или коротко:
(или коротко: 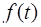 l
l 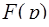 ).
).
Применение этого равенства приводит к известным формулам изображений элементарных функций, согласно которым
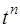 l
l 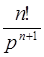 ,
, 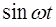 l
l 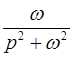 ,
, 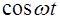 l
l 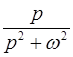 ,
,
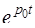 l
l 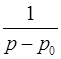 ,
, 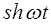 l
l 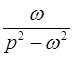 ,
, 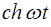 l
l 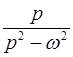 .
.
Замечание. На самом деле здесь перечислены изображения элементарных функций, умноженных на единичную функцию Хевисайда 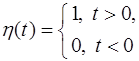 , которую обычно не пишут. Сама же функция Хевисайда имеет изображение
, которую обычно не пишут. Сама же функция Хевисайда имеет изображение 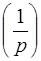 .
.
Так как изображение суммы оригиналов равно сумме изображений, получаем
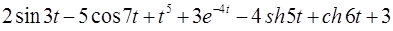 l
l
l 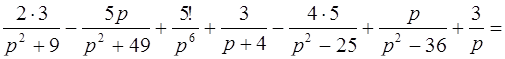
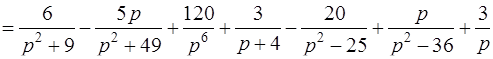 .
.
Задача 84. Найти изображение F ( p ) для функции-оригинала
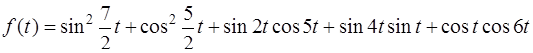 .
.
Решение. Преобразуем f ( t ) с помощью формул элементарной математики [приложение 5]:
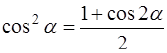 ,
, 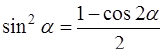 ,
,
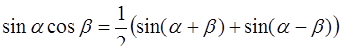 ,
,
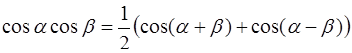 ,
,
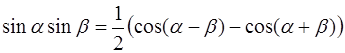 .
.
В результате получим
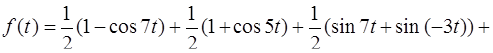
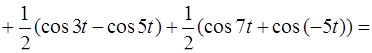
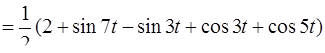 .
.
Теперь можно применить формулы изображений элементарных функций [приложение 6]. Имеем
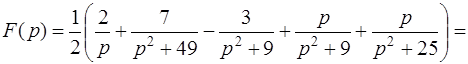
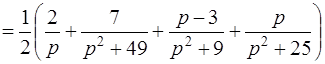 .
.
Задача 85. Найти функцию-оригинал f ( t ) по заданному изображению
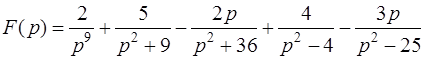 .
.
Решение. Воспользуемся формулами связи функций-оригиналов и их изображений [приложение 6]. Получим
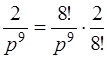 l
l 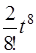 ,
, 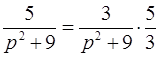 l
l 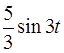 ,
, 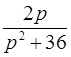 l
l 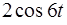 ,
, 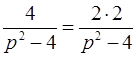 l
l 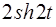 ,
, 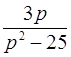 l
l 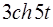 .
.
Окончательно имеем
 .
.
Задача 86. Найти изображение свертки функций:
1) 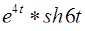 ; 2)
; 2) 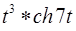 ; 3)
; 3) 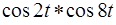 .
.
Решение. Согласно теореме Бореля свертка (обозначается 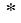 ) функций f ( t )
) функций f ( t ) 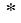 g ( t ) имеет изображением функцию F ( p ) ·G ( p ) (здесь
g ( t ) имеет изображением функцию F ( p ) ·G ( p ) (здесь 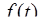 l
l 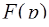 ,
, 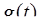 l
l 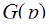 ). Значит, для получения искомого изображения достаточно перемножить изображения каждой из свертываемых функций. Используя формулы изображений элементарных функций [приложение 6], получим
). Значит, для получения искомого изображения достаточно перемножить изображения каждой из свертываемых функций. Используя формулы изображений элементарных функций [приложение 6], получим
1) 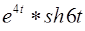 l
l 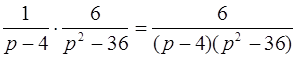 ;
;
2) 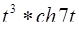 l
l 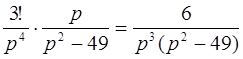 ;
;
3) 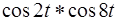 l
l 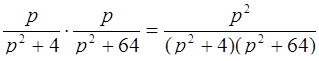 .
.
Задача 87. Средствами операционного исчисления решить дифференциальное уравнение
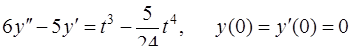 .
.
Решение. Считая искомую функцию y ( t ) функцией-оригиналом, обозначим ее изображение Y ( p ) и найдем изображения левой и правой частей дифференциального уравнения. Согласно формуле дифференцирования оригинала
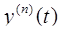 l
l 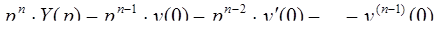
и с учетом нулевых начальных условий получим
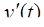 l
l 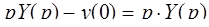 ,
,
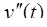 l
l 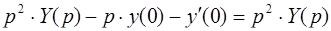 .
.
Так как 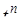 l
l 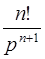 [приложение 6], для правой части имеем
[приложение 6], для правой части имеем
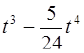 l
l 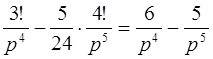 .
.
В результате дифференциальное уравнение, записанное в изображениях, примет вид
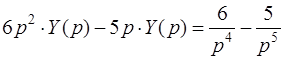 .
.
Решаем его относительно 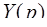 :
:
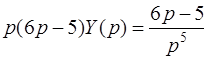 , т.е.
, т.е. 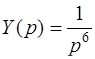 .
.
Возвращаясь от изображения Y ( p ) к оригиналу y ( t ), получим искомое решение дифференциального уравнения
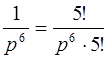 l
l 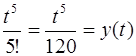 .
.
Теория вероятностей
Рассматриваются задачи по темам: алгебра событий; формула полной вероятности; дискретная случайная величина и ее характеристики; непрерывная случайная величина и ее характеристики; распределения случайной величины: биномиальное, нормальное.
Задача 88. Три стрелка стреляют по мишени с вероятностями попадания 0,8, 0,9 и 0,7 соответственно. Найти вероятность того, что при одном залпе в мишень
а) попадут все три стрелка; б) не попадет ни один;
в) попадет ровно один стрелок; г) попадет хотя бы один стрелок.
Решение. Обозначим А1, А2 и А3 − попадания в мишень первым, вторым и третьим стрелками соответственно, а 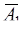 ,
, 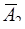 и
и 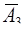 − непопадания для этих же стрелков. Так как произведение событий есть событие, состоящее в совместном появлении перемножаемых величин, то А1А2А3 означает три попадания, а
− непопадания для этих же стрелков. Так как произведение событий есть событие, состоящее в совместном появлении перемножаемых величин, то А1А2А3 означает три попадания, а 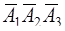 − три промаха.
− три промаха.
События А1, А2, А3 независимы (появление одного не влияет на вероятность появления другого), поэтому вероятность трех попаданий (случай а)) равна произведению вероятностей
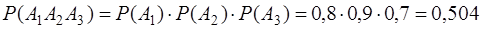 .
.
События А1 и 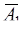 − противоположные события, значит удовлетворяют соотношению
− противоположные события, значит удовлетворяют соотношению
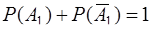 .
.
Но тогда 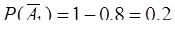 . Аналогично,
. Аналогично,
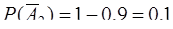 ,
, 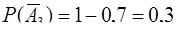 .
.
Таким образом, вероятность трех промахов (случай б)) равна
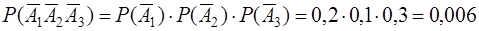 .
.
Рассмотрим случай в). Искомое событие − попадет ровно один стрелок − состоит в появлении одного из событий:
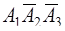 (первый попал в мишень, а второй и третий промахнулись),
(первый попал в мишень, а второй и третий промахнулись),
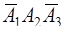 (второй попал, а два других промахнулись),
(второй попал, а два других промахнулись),
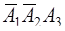 (третий попал, остальные − нет).
(третий попал, остальные − нет).
Так как событие, состоящее в появлении хотя бы одного из событий, есть их сумма, получим, что искомое событие равно
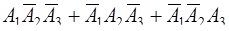 .
.
Слагаемые этой суммы − несовместные события (появление одного из них исключает появление другого), поэтому вероятность суммы равна сумме вероятностей. Следовательно, вероятность того, что попадет ровно один стрелок, равна
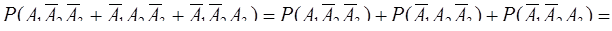
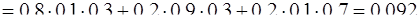 .
.
Рассматривая случай г), обозначим В − событие, состоящее в том, что в мишень попадет хотя бы один стрелок, т.е. при одном залпе будет от одного до трех попаданий. Если к событию В добавить событие, означающее все три промаха, получим полную группу событий с вероятностью, равной 1. Но тогда событие, означающее три промаха, есть 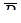 , а его вероятность уже найдена (случай б)).
, а его вероятность уже найдена (случай б)).
Итак,
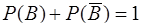 и
и 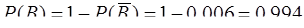 .
.
Задача 89. В ящике содержится 10 деталей, изготовленных на заводе №1, 15 деталей, изготовленных на заводе №2 и 20 деталей, изготовленных на заводе №3. Вероятности брака для трех заводов соответственно равны 0,1, 0,3 и 0,2. Найти вероятность того, что наудачу взятая деталь окажется бракованной.
Решение. Обозначим А − событие, состоящее в том, что взятая деталь бракованная. Возможны три предположения (гипотезы):
Н1 − деталь изготовлена на заводе №1,
Н2 − деталь изготовлена на заводе №2,
Н3 − деталь изготовлена на заводе №3.
Вероятности этих гипотез равны
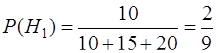 ,
, 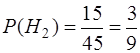 ,
, 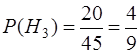 .
.
По формуле полной вероятности (с учетом всех гипотез)
 .
.
Здесь 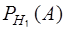 − вероятность того, что взятая деталь является бракованной при условии, что она изготовлена на заводе №1. Согласно условию задачи
− вероятность того, что взятая деталь является бракованной при условии, что она изготовлена на заводе №1. Согласно условию задачи 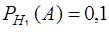 . Аналогично,
. Аналогично, 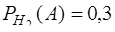 ,
, 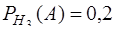 .
.
Но тогда
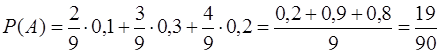 .
.
Задача 90. Дискретная случайная величина Х задана законом распределения
| Х | 1 | 3 |
| р | 0,8 | р2 |
Найти математическое ожидание M ( X ) и дисперсию D (Х) случайной величины Х.
Решение. Найдем р2 из условия
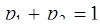 .
.
Получим
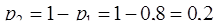 .
.
Для дискретной случайной величины
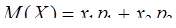 ,
, 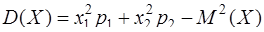 .
.
Поэтому
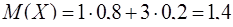 ,
,
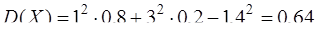 .
.
Задача 91. Дискретная случайная величина задана законом распределения
| Х | 1 | 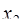
| 5 |
| р | р1 | 0,3 | 0,4 |
Найти х2, если М(Х) = 2,9.
Решение. Так как 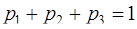 , то
, то
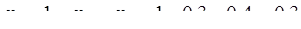 .
.
В формулу математического ожидания
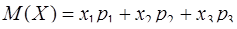
подставим известные значения и найдем х2
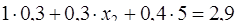 ,
,
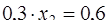 ,
,
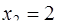 .
.
Задача 92. Задана плотность распределения f ( x ) непрерывной случайной величины Х:
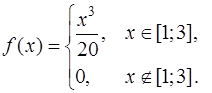
Найти 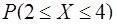 .
.
Решение. Вероятность попадания непрерывной случайной величины на отрезок [a , b] определяется формулой
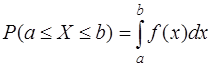 .
.
Поскольку на отрезке [2, 4] плотность распределения f ( x ) задана различными аналитическими выражениями, интеграл заменяется суммой интегралов и тогда
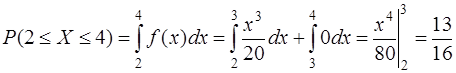 .
.
Задача 93. Непрерывная случайная величина Х задана функцией распределения 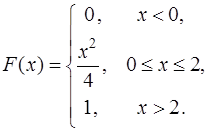
Найти М(Х), D(Х).
Решение. Найдем сначала плотность распределения f ( x ) непрерывной случайной величины Х по формуле
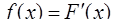 .
.
Получим
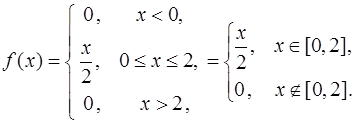
Математическое ожидание М(Х) и дисперсия D(Х) непрерывной случайной величины X вычисляются по формулам
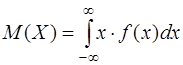 ,
, 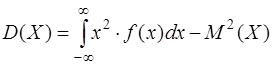 .
.
Получаем
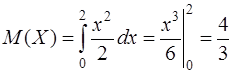 ,
,
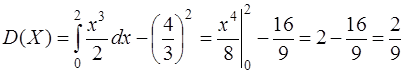 .
.
Задача 94. Случайная величина Х − число появлений события А в n испытаниях − распределена по биномиальному закону с математическим ожиданием М(Х) = 4 и дисперсией D(Х) = 3. Найти вероятность появления события А в каждом испытании.
Решение. Для случайной величины, распределенной по биномиальному закону, справедливы формулы
М(Х) = np, D(Х) = npq,
где р − вероятность появления события А в каждом испытании, а q – вероятность противоположного события, q =1 − p.
Имеем: np = 4, npq = 3.
Разделив второе равенство на первое, найдем q:
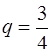 , отсюда
, отсюда 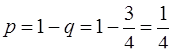 .
.
Задача 95. Найти дисперсию случайной величины Х − числа появлений события А в 20 независимых испытаниях, если вероятности появления события в каждом испытании одинаковы, а М(Х) = 2.
Решение. Так как испытания независимы, а вероятность появления события А в каждом испытании одинакова, то случайная величина распределена по биномиальному закону. Но тогда
М(Х) = np, D(Х) = npq.
Из первого равенства найдем
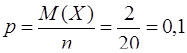 .
.
Тогда 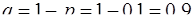 ,
,
значит, 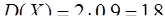 .
.
Задача 96. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами М(Х) = 2 см, D(Х) = 0,25 см2. Деталь считается годной, если ее диаметр не менее 1,5 см и не более 3 см. Определить процент годных и процент бракованных деталей.
Решение. Вероятность того, что непрерывная случайная величина Х, распределенная по нормальному закону, примет значение, принадлежащее отрезку 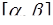 , равна
, равна
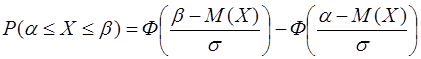 ,
,
где 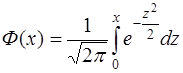 − функция Лапласа,
− функция Лапласа,
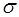 − среднее квадратическое отклонение (
− среднее квадратическое отклонение ( 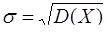 ).
).
Поэтому
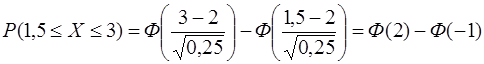
или, с учетом нечетности функции Лапласа,
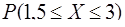
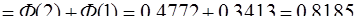
(значения функции Лапласа можно найти в таблице приложений – см. библ. список [2, 3]).
Полученный результат означает, что процент годных деталей составит 81,85%, бракованных − 18,15%.
Задача 97. Дальность полета снаряда распределена нормально с математическим ожиданием 200 м и средним квадратическим отклонением 10 м. Определить интервал, в который согласно «правилу 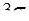 » попадет снаряд с вероятностью 0,9973.
» попадет снаряд с вероятностью 0,9973.
Решение. Если в формуле вероятности попадания нормально распределенной случайной величины на отрезок 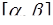 (см. задачу 96) принять
(см. задачу 96) принять 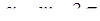 ,
, 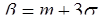 , окажется, что
, окажется, что
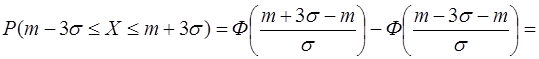
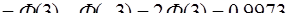 .
.
Это и есть «правило 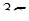 » − более 99,7% значений случайной величины попадут в интервал радиуса
» − более 99,7% значений случайной величины попадут в интервал радиуса 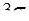 , симметричный относительно математического ожидания.
, симметричный относительно математического ожидания.
С учетом данных задачи получим
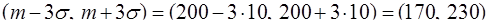 .
.
Приложение 1
Дата: 2019-03-05, просмотров: 317.