Рассматриваются следующие задачи: вычисление пределов, дифференцирование функций одной и нескольких переменных, приложения дифференциального исчисления к исследованию функций.
Задача 27. Вычислить 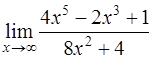 .
.
Решение. При 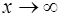 числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность
числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность 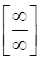 . Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:
. Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:
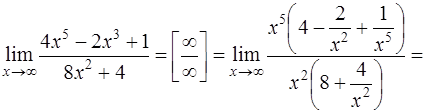
 .
.
При 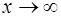 величины
величины 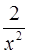 ,
, 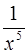 ,
,  стремятся к 0,
стремятся к 0,  , весь числитель стремится к
, весь числитель стремится к  , а знаменатель
, а знаменатель 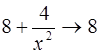 . Поэтому вся дробь стремится к
. Поэтому вся дробь стремится к  .
.
Таким образом,
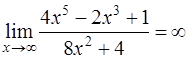
Задача 28. Вычислить 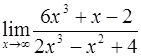 .
.
Решение. При 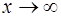 числитель и знаменатель стремятся к
числитель и знаменатель стремятся к 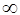 . Это неопределенность вида
. Это неопределенность вида 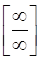 . Раскрываем ее (см. задачу 27):
. Раскрываем ее (см. задачу 27):

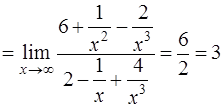 .
.
Задача 29. Вычислить 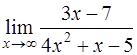 .
.
Решение. Поскольку числитель и знаменатель при  стремятся к
стремятся к 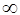 , имеем неопределенность
, имеем неопределенность 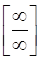 . Раскрываем ее (см. задачу 27):
. Раскрываем ее (см. задачу 27):
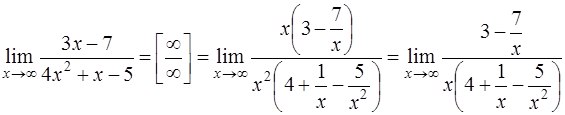 .
.
Так как при 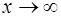 числитель стремится к 3, а знаменатель − к
числитель стремится к 3, а знаменатель − к  , то вся дробь стремится к 0 и
, то вся дробь стремится к 0 и
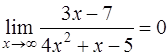 .
.
Замечание. Полученные в задачах 27-29 результаты можно обобщить следующим образом:
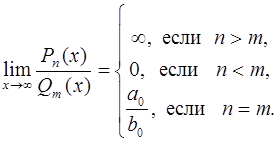
Здесь 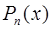 и
и 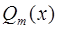 - многочлены степеней n и m соответственно, причем
- многочлены степеней n и m соответственно, причем
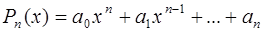 ,
, 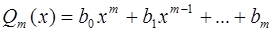 .
.
Это правило позволяет сразу получить результат, минуя вычисления, одним лишь сравнением старших степеней многочленов 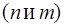 числителя и знаменателя (в задаче 27: 5>2, значит, предел равен
числителя и знаменателя (в задаче 27: 5>2, значит, предел равен 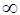 ; в задаче 28: 3 = 3, значит, предел равен
; в задаче 28: 3 = 3, значит, предел равен 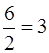 ; в задаче 29: 1 < 2, значит, предел равен 0).
; в задаче 29: 1 < 2, значит, предел равен 0).
Задача 30. Вычислить 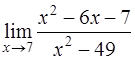 .
.
Решение. При 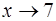 числитель и знаменатель дроби стремятся к 0. Это неопределенность вида
числитель и знаменатель дроби стремятся к 0. Это неопределенность вида  . Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7) (из-за которого и возникла неопределенность), получим
. Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7) (из-за которого и возникла неопределенность), получим
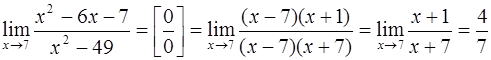 .
.
Задача 31. Вычислить 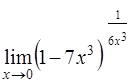 .
.
Решение. Так как при 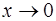 выражение
выражение  стремится к 1, а показатель степени
стремится к 1, а показатель степени 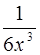 − к бесконечности, имеем неопределенность
− к бесконечности, имеем неопределенность 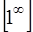 . Раскрываем ее с помощью второго замечательного предела
. Раскрываем ее с помощью второго замечательного предела
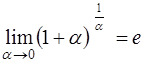 .
.
Считая  , достраиваем выражение до второго замечательного предела и получаем
, достраиваем выражение до второго замечательного предела и получаем
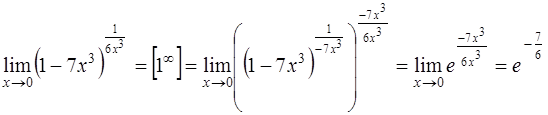 .
.
Задача 32. Вычислить 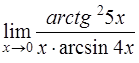 .
.
Решение. Поскольку при 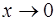 числитель и знаменатель дроби стремятся к 0, имеем неопределенность
числитель и знаменатель дроби стремятся к 0, имеем неопределенность  . Воспользовавшись формулами таблицы эквивалентности [приложение 4] для бесконечно малой величины
. Воспользовавшись формулами таблицы эквивалентности [приложение 4] для бесконечно малой величины 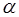 (
( 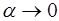 ):
):
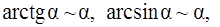
получим при 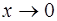 :
:
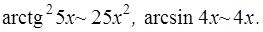
Заменяя числитель и знаменатель на эквивалентные бесконечно малые величины, найдем
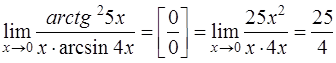 .
.
Задача 33. Вычислить 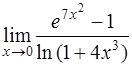 .
.
Решение. Имеем неопределенность 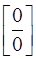 . Согласно формулам таблицы эквивалентности [приложение 4] для бесконечно малой величины
. Согласно формулам таблицы эквивалентности [приложение 4] для бесконечно малой величины 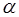 (
( 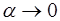 )
)
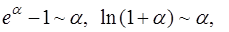
поэтому при 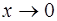 :
: 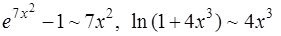 .
.
Тогда
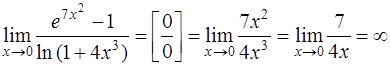 .
.
Задача 34. Найти 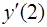 , если
, если  .
.
Решение. Применяя формулы дифференцирования суммы, произведения и частного [приложение 4]:
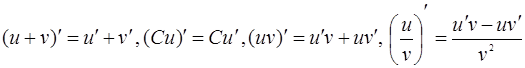 ,
,
где 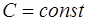 , имеем
, имеем

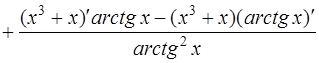
и далее, с учетом формул дифференцирования элементарных функций (2),(5), (13) [приложение 4]
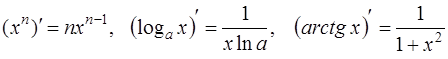
получим
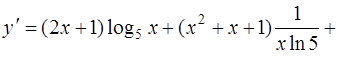
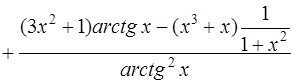 .
.
Подставим в производную х = 2:
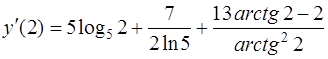 .
.
Задача 35. Для функции  найти
найти  .
.
Решение. Применим правило дифференцирования сложной функции: если 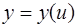 ,
, 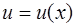 , то
, то 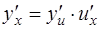 .
.
В данном случае 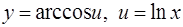 . Согласно формулам (12), (6) [приложение 4]
. Согласно формулам (12), (6) [приложение 4]
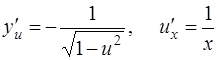 .
.
Тогда
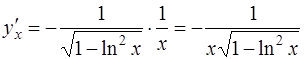 .
.
Задача 36. Для функции 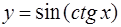 найти
найти  .
.
Решение. По правилу дифференцирования сложной функции  , где
, где 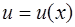 , имеем
, имеем 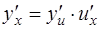 .
.
Так как 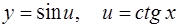 , применяем формулы (7), (10) [приложение 4] :
, применяем формулы (7), (10) [приложение 4] :
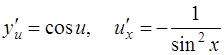 .
.
Окончательно,
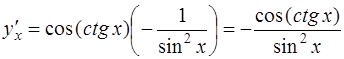 .
.
Задача 37. Дана функция 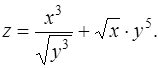 Найти ее частные производные
Найти ее частные производные 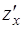 и
и  в точке
в точке 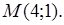
Решение. Преобразуем данную функцию к виду
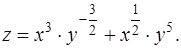
Вычислим частную производную 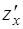 , используя формулу дифференцирования (2) [приложение 4]
, используя формулу дифференцирования (2) [приложение 4]

и считая у константой:
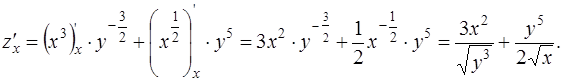
Подставив вместо х и у координаты точки 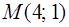 , получим
, получим
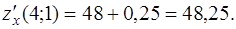
Найдем 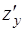 , считая х константой:
, считая х константой:
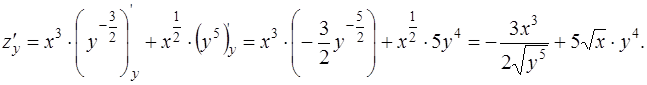
Подставляя координаты точки 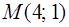 , получим
, получим

Задача 38. Найти интервалы возрастания и убывания функции  .
.
Решение. Функция y = f ( x ) возрастает, если 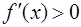 , и убывает, если
, и убывает, если 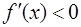 . Найдем
. Найдем  :
:
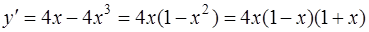 .
.
Определим знаки первой производной  и промежутки монотонности функции у
и промежутки монотонности функции у
| x | 
| −1 | 
| 0 | 
| 1 | 
|

| + | 0 | − | 0 | + | 0 | − |
| y |  
| 
| 
| 
|
Итак, функция возрастает на интервалах 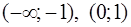 и убывает на интервалах
и убывает на интервалах 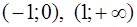 .
.
Задача 39. Найти интервалы выпуклости и вогнутости функции 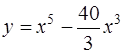 .
.
Решение. Функция выпукла, если 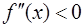 и вогнута, если
и вогнута, если 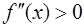 . Найдем
. Найдем 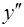 :
:
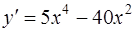 ,
,
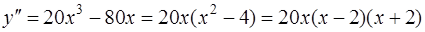 .
.
Определим знаки второй производной 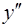 и промежутки выпуклости и вогнутости функции у
и промежутки выпуклости и вогнутости функции у
| x | 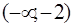
| −2 | 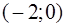
| 0 | 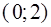
| 2 | 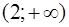
|
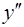
| − | 0 | + | 0 | − | 0 | + |
| y | 
| 
| 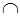
| 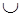
|
Таким образом, функция выпукла при 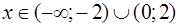 и вогнута при
и вогнута при 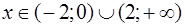 .
.
ГЛАВА 2
Интегралы, РЯДЫ,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Интегралы
Рассматриваются следующие задачи: вычисление неопределенного интеграла, определенного интеграла, вычисление площадей плоских фигур.
Задача 40. Вычислить интеграл 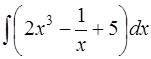 .
.
Решение. Воспользуемся основными свойствами неопределенного интеграла (интеграл от суммы равен сумме интегралов, а постоянный множитель можно выносить за знак интеграла) и применим формулы (2), (3) и (1) из таблицы интегралов [приложение 5]:
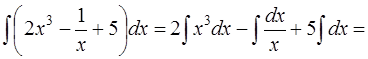
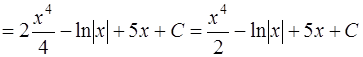 .
.
Задача 41. Вычислить интеграл  .
.
Решение. Данный интеграл является определенным. Для его вычисления необходимо воспользоваться формулой Ньютона–Лейбница [приложение 5]
 ,
,
где 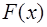 - какая-либо первообразная для непрерывной функции
- какая-либо первообразная для непрерывной функции 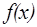 .
.
Тогда в соответствии с формулой (2) [приложение 5] имеем

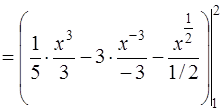
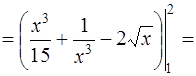
 .
.
Задача 42. Вычислить интеграл 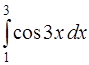 .
.
Решение. Интеграл можно свести к табличному (7) [приложение 5], если сделать замену переменной, приняв 3х = t. Дифференцируя обе части равенства, получим
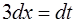 , или
, или 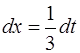 .
.
Так как интеграл определенный, необходимо также изменить пределы интегрирования. При этом получим
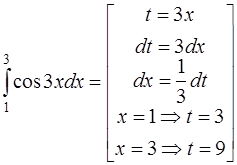 =
= 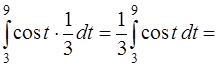
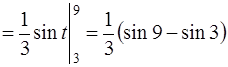 .
.
Замечание. Задачу можно было решить, используя правило: если
 , то
, то 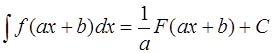 .
.
В данном случае так как
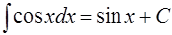 , то
, то  ,
,
Поэтому 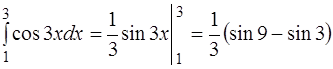 .
.
Задача 43. Вычислить интеграл 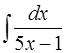 .
.
Решение. Интеграл можно свести к табличному (3) [приложение 5] , если выполнить замену: t = 5х – 1. Тогда
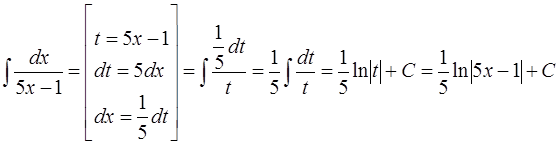 .
.
Задача 44. Вычислить интеграл 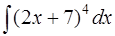 .
.
Решение. Интеграл можно свести к табличному (2) [приложение 5], если сделать замену переменной: t = 2х + 7.
Но можно использовать замечание к задаче 42. В этом случае поскольку  , имеем
, имеем
 .
.
Задача 45. Вычислить интеграл 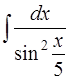 .
.
Решение. Интеграл можно свести к табличному (9) [приложение 5] с помощью замены t = х / 5:
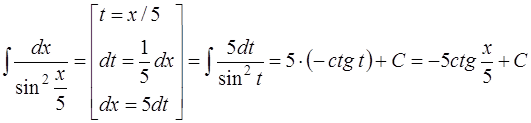 .
.
Задача 46. Вычислить интеграл  .
.
Решение. Интеграл можно свести к табличному (4) [приложение 5] заменой t = 6х. Так как интеграл определенный, изменяем и пределы интегрирования:
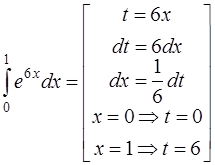 =
= 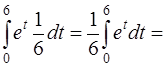
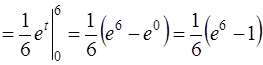 .
.
Задача 47. Вычислить интеграл 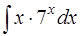 .
.
Решение. Интеграл относится к группе интегралов: 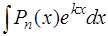 ,
,  ,
, 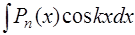 , где Pn(x) – многочлен степени п. Вычисление таких интегралов выполняется интегрированием по частям [приложение 5]
, где Pn(x) – многочлен степени п. Вычисление таких интегралов выполняется интегрированием по частям [приложение 5]

Если за и принять многочлен Pn(x), то в результате применения формулы интегрирования по частям интеграл упростится (уменьшится степень многочлена).
Обозначим 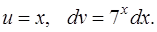 Найдем
Найдем 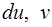 :
:

(формула интегрирования (5) [приложение 5]). Тогда
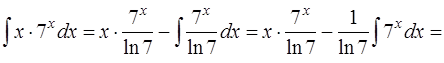
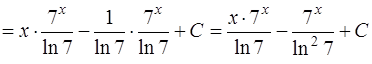 .
.
Задача 48. Вычислить интеграл 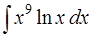 .
.
Решение. Этот интеграл относится к группе интегралов вида 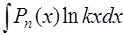 ,
, 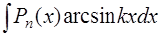 ,
, 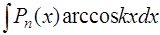 ,
, 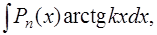
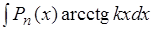 (Pn(x) – многочлен степени п) и вычисляется по формуле интегрирования по частям [приложение 5].
(Pn(x) – многочлен степени п) и вычисляется по формуле интегрирования по частям [приложение 5].
В результате применения этой формулы исходный интеграл упростится, если за и принимать функции 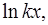

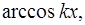
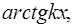
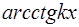 .
.
Итак, положим
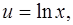
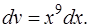
Тогда
 .
.
Получаем
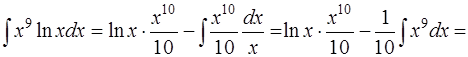
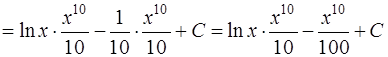 .
.
Задача 49. Вычислить интеграл 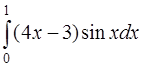 .
.
Решение. Для определенного интеграла также применима формула интегрирования по частям
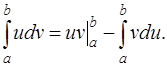
Положим 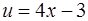 ,
, 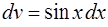 (см. задачу 47). Тогда
(см. задачу 47). Тогда
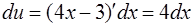 и
и 
(формула интегрирования (6) [приложение 5]).
Итак,
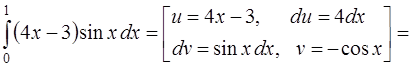
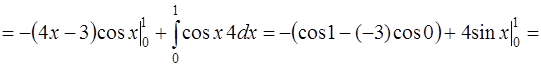
 .
.
Задача 50. Вычислить интеграл 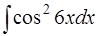 .
.
Решение. Это интеграл вида 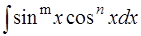 с чётными m и n (в данном случае
с чётными m и n (в данном случае 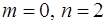 ) и вычисляется с помощью формул тригонометрии [приложение 5].
) и вычисляется с помощью формул тригонометрии [приложение 5].
Воспользуемся формулой понижения степени [приложение 5]
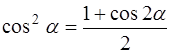 ,
,
получим

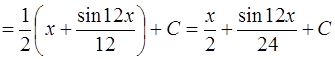
(формулы интегрирования (1), (7) [приложение 5]).
Задача 51. Вычислить 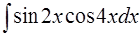 .
.
Решение. Применяя тригонометрическую формулу [приложение 5]
 ,
,
получим
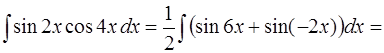
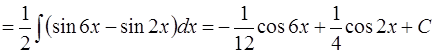
(формула интегрирования (6) [приложение 5]).
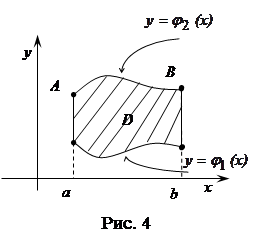
Задача 52. Вычислить площадь области D, ограниченной линиями  , y = x – 1, x = 0, x = 2.
, y = x – 1, x = 0, x = 2.
Решение. Площадь области D, ограниченной линиями  ,
,  , x = а, x = b (рис. 4), вычисляется по формуле
, x = а, x = b (рис. 4), вычисляется по формуле
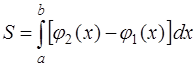 .
.
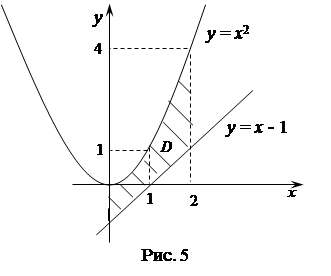
Построим заданную область D (рис. 5). Слева область ограничена прямой  , справа – прямой
, справа – прямой 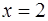 , снизу – прямой
, снизу – прямой  , сверху – параболой
, сверху – параболой  .
.
Подставляя все данные в формулу, найдем площадь области D:
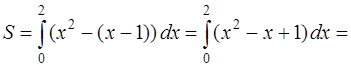
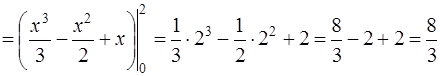 (кв. ед.)
(кв. ед.)
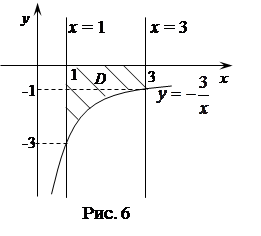 Задача 53. Вычислить площадь области D, ограниченной линиями
Задача 53. Вычислить площадь области D, ограниченной линиями 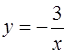 , y = 0, x = 1, x = 3.
, y = 0, x = 1, x = 3.
Решение. Построим заданную область D (рис. 6), ограниченную слева – прямой  , справа – прямой
, справа – прямой 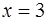 , снизу – параболой
, снизу – параболой 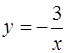 , сверху – прямой
, сверху – прямой 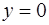 .
.
Подставляя все данные в формулу площади (см. задачу 52), получим
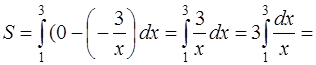
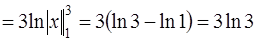 (кв. ед.)
(кв. ед.)
Ряды
Рассматриваются задачи о сходимости положительных, знакопеременных и функциональных рядов.
Задача 54. Исследовать на сходимость ряд 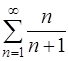 .
.
Решение. Необходимый признак сходимости ряда гласит [приложение 5 – РЯДЫ]: Если ряд 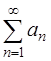 сходится, то
сходится, то 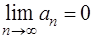 (если же
(если же 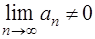 , то ряд расходится).
, то ряд расходится).
Здесь 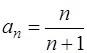 . Рассмотрим предел
. Рассмотрим предел
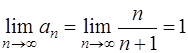 .
.
Предел не равен нулю, следовательно, ряд расходится.
Задача 55. Исследовать на сходимость ряд 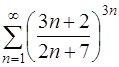 .
.
Решение. Используем радикальный признак Коши [приложение 5 – РЯДЫ]: Если для положительного ряда 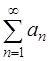 существует предел
существует предел
 , то
, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b = 1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Найдем предел
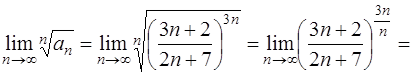
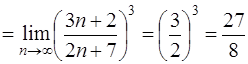 .
.
Найденный предел 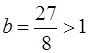 . Следовательно, данный ряд расходится.
. Следовательно, данный ряд расходится.
Задача 56. Исследовать на сходимость ряд  .
.
Решение. Используем признак Даламбера [приложение 5 – РЯДЫ]: Если для положительного ряда 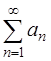 существует предел
существует предел
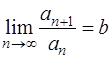 , то
, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b = 1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Здесь  ,
,  , тогда имеем
, тогда имеем
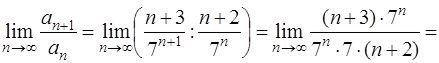
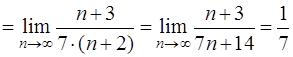 .
.
Найденный предел 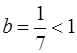 . Следовательно, данный ряд сходится.
. Следовательно, данный ряд сходится.
Задача 57. Исследовать на сходимость ряд 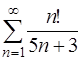 .
.
Решение. Применяем признак Даламбера (см. задачу 56). Здесь 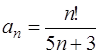 ,
, 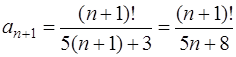 , поэтому
, поэтому
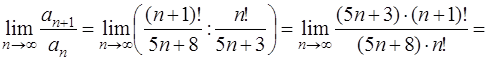
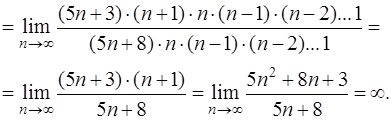
Найденный предел 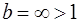 . Следовательно, ряд расходится.
. Следовательно, ряд расходится.
Задача 58. Исследовать на сходимость ряд 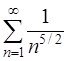 .
.
Решение. Ряд 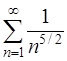 – это обобщенный гармонический ряд вида
– это обобщенный гармонический ряд вида 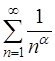 , где
, где 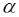 – действительное число. Известно, что такой ряд [приложение 5 – РЯДЫ]
– действительное число. Известно, что такой ряд [приложение 5 – РЯДЫ]
1) сходится при 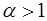 ;
;
2) расходится при 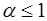 .
.
Так как в исходном примере 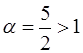 , то ряд сходится.
, то ряд сходится.
Задача 59. Исследовать на сходимость ряд  .
.
Решение. При исследовании сходимости ряда  можно воспользоваться предельным признаком сравнения положительных рядов [приложение 5 – РЯДЫ]: Если существует конечный и отличный от нуля предел
можно воспользоваться предельным признаком сравнения положительных рядов [приложение 5 – РЯДЫ]: Если существует конечный и отличный от нуля предел 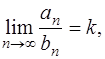 то положительные ряды
то положительные ряды 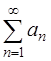 и
и 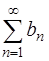 одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Для сравнения возьмем обобщенный гармонический ряд  . Он сходится (см. задачу 58). Применяя предельный признак сравнения, получим
. Он сходится (см. задачу 58). Применяя предельный признак сравнения, получим
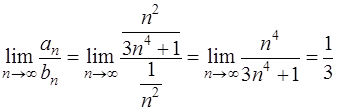 .
.
Так как предел  конечен и отличен от нуля, то ряд
конечен и отличен от нуля, то ряд 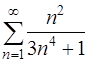 также сходится.
также сходится.
Задача 60. Исследовать на сходимость ряд 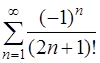 .
.
Решение. Этот ряд относится к знакочередующимся рядам вида
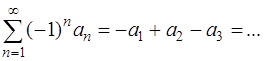 ,
,
где 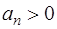 (n = 1, 2, 3…).
(n = 1, 2, 3…).
Cогласно признаку Лейбница [приложение 5 – РЯДЫ] такой ряд сходится, если выполняются два условия:
1) 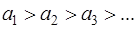 ; 2)
; 2) 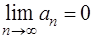 .
.
Для данного ряда имеем: 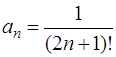 .
.
Условия теоремы выполнены:
1) 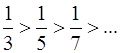 ; 2)
; 2) 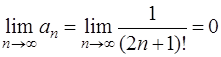 .
.
Следовательно, ряд 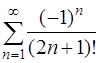 сходится.
сходится.
Рассматриваемый ряд является частным случаем знакопеременного (с произвольным чередованием знаков) ряда. Сходимость знакопеременного ряда может быть абсолютной или условной в зависимости от того, сходится или расходится соответствующий ряд из абсолютных величин членов знакопеременного ряда.
Пусть  – знакопеременный ряд. Если сходится ряд
– знакопеременный ряд. Если сходится ряд 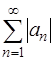 , составленный из модулей, то ряд
, составленный из модулей, то ряд  называется абсолютно сходящимся. Может оказаться, что ряд
называется абсолютно сходящимся. Может оказаться, что ряд 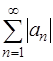 расходится, а ряд
расходится, а ряд  сходится. В этом случае ряд
сходится. В этом случае ряд  называется условно сходящимся.
называется условно сходящимся.
Итак, рассмотрим ряд, составленный из абсолютных величин членов данного ряда
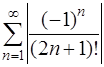 =
= 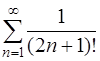 .
.
Он положительный. Исследуем его на сходимость по признаку Даламбера [приложение 5 – РЯДЫ].
Так как 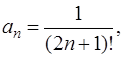
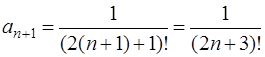 , получим
, получим
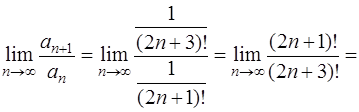
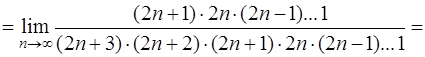
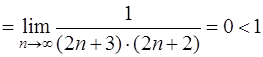 .
.
Тогда ряд 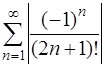 сходится, следовательно, ряд
сходится, следовательно, ряд 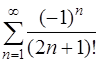 сходится абсолютно.
сходится абсолютно.
Задача 61. Исследовать на сходимость ряд 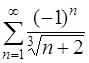 .
.
Решение. Для данного ряда выполняются условия признака Лейбница [приложение 5 – РЯДЫ]:
1)  2)
2) 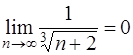 .
.
Значит, ряд сходится. Исследуя ряд на абсолютную сходимость (см. задачу 60), составим ряд из модулей
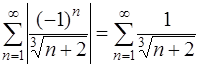 .
.
Для сравнения возьмем обобщенный гармонический расходящийся ряд 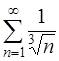 и воспользуемся предельным признаком сравнения [приложение 5 – РЯДЫ]:
и воспользуемся предельным признаком сравнения [приложение 5 – РЯДЫ]:
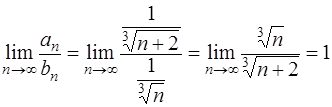 .
.
Так как предел конечен и отличен от нуля, то ряды
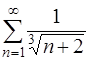 и
и 
ведут себя одинаково в смысле сходимости, т.е. ряд 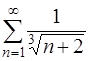 тоже расходится. Итак, ряд
тоже расходится. Итак, ряд 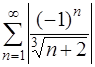 расходится, следовательно, ряд
расходится, следовательно, ряд 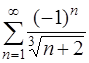 сходится условно.
сходится условно.
Задача 62. Исследовать на сходимость ряд  .
.
Решение. Если ряд 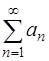 сходится, то
сходится, то 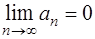 (см. задачу 54). Но
(см. задачу 54). Но 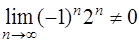 (этот предел не существует), поэтому ряд
(этот предел не существует), поэтому ряд  расходится.
расходится.
Задача 63. Исследовать на сходимость ряд 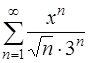 .
.
Решение. Ряд вида
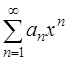 ,
,
где а0, а1, а2, …, а n, … – постоянные вещественные числа, называется степенным рядом. Степенной ряд – это частный случай функционального ряда 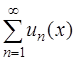 , то есть ряда, члены которого есть функции, зависящие от х.
, то есть ряда, члены которого есть функции, зависящие от х.
Для каждого степенного ряда существует положительное число R такое, что этот ряд абсолютно сходится, если 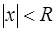 и расходится, если
и расходится, если 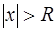 . Число R называется радиусом сходимости рассматриваемого ряда, а интервал (– R, R) – интервалом сходимости этого ряда.
. Число R называется радиусом сходимости рассматриваемого ряда, а интервал (– R, R) – интервалом сходимости этого ряда.
На концах интервала сходимости (в точках х = – R и х = R) степенной ряд может сходиться или расходиться. Это выясняется отдельно для каждого числового ряда, получающегося из степенного ряда в результате подстановки в него указанных значений.
Радиус сходимости R степенного ряда можно определить с помощью признака Даламбера или радикального признака Коши по формулам [приложение 5 – РЯДЫ]:
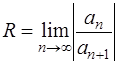 ,
, 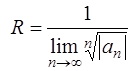 .
.
Найдем радиус сходимости для заданного ряда по первой формуле. Так как
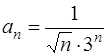 ,
, 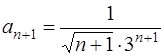 ,
,
получим
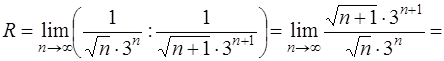
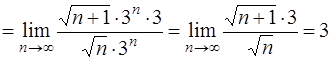 .
.
Следовательно, R = 3. Поэтому данный ряд абсолютно сходится в интервале (– 3; 3) и расходится вне отрезка [– 3; 3].
Исследуем сходимость ряда в точках х = 3 и х = – 3.
При х = 3 исходный ряд принимает вид
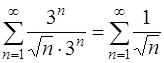 .
.
Это обобщенный гармонический расходящийся ряд ( 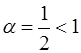 ) [приложение 5 – РЯДЫ]. Итак, при х = 3 заданный ряд расходится.
) [приложение 5 – РЯДЫ]. Итак, при х = 3 заданный ряд расходится.
При х = – 3 получаем знакочередующийся ряд
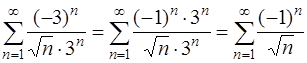 .
.
Рассмотрим для него выполнение условий теоремы Лейбница [приложение 5 – РЯДЫ]
1) 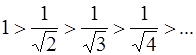 ; 2)
; 2) 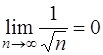 .
.
Условия выполняются, значит, ряд 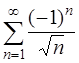 сходится.
сходится.
Следовательно, область сходимости исходного ряда [– 3; 3).
Задача 64. Исследовать на сходимость ряд 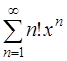 .
.
Решение. Этот ряд степенной. Будем искать радиус сходимости ряда по формуле
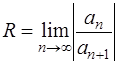 (см. задачу 63).
(см. задачу 63).
Так как 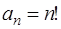 ,
, 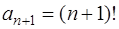 , то
, то
 .
.
Это означает, что областью сходимости ряда может быть только одна точка х = 0. Действительно, при х = 0 получим нулевой сходящийся ряд
0 + 0 + 0 + … .
Итак, ряд 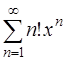 сходится в одной точке х = 0.
сходится в одной точке х = 0.
Задача 65. Исследовать на сходимость ряд 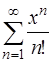 .
.
Решение. В соответствии с теорией, изложенной в задаче 63, будем искать радиус сходимости ряда по формуле
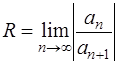 .
.
Так как 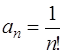 ,
, 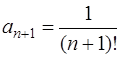 , то
, то
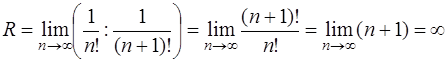 .
.
Следовательно, 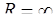 . Значит, ряд сходится при любых х и область сходимости ряда
. Значит, ряд сходится при любых х и область сходимости ряда 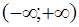 .
.
§ 3. Дифференциальные уравнения
Рассматриваются дифференциальные уравнения первого порядка (с разделяющимися переменными, однородные, линейные), однородные дифференциальные уравнения высших порядков с постоянными коэффициентами, задача Коши.
Задача 66. Найти общее решение дифференциального уравнения
 .
.
Решение. Уравнение, содержащее переменную, функцию этой переменной, а также производные этой функции, называется дифференциальным. Решить дифференциальное уравнение – значит найти функцию у(х), обращающую уравнение в тождество.
В данном уравнении можно разделить переменные, то есть с помощью преобразований сделать так, чтобы в одной части было выражение, зависящее только от х, а в другой – только от у. Такие уравнения называются дифференциальными уравнениями с разделяющимися переменными.
Перепишем уравнение, используя другое обозначение для производной: 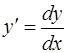 . Получим
. Получим
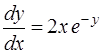 .
.
Разделим переменные, умножив уравнение на выражение 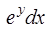 . Это приведет к равенству
. Это приведет к равенству
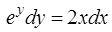 .
.
Проинтегрируем обе части полученного уравнения
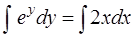 ,
,
вычислим интегралы с помощью формул интегрирования (4) и (2) [приложение 5]
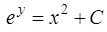
и выразим у 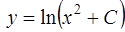 .
.
Получившееся выражение называется общим решением дифференциального уравнения.
Задача 67. Найти общее решение дифференциального уравнения
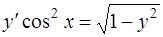 .
.
Решение. Данное дифференциальное уравнение также относится к уравнениям с разделяющимися переменными и решается аналогично задаче 66. Перепишем уравнение в виде
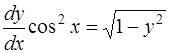 .
.
Разделим переменные, умножив обе части уравнения на  :
:
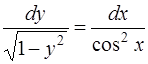 .
.
В результате вычисления интегралов
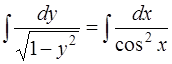
по формулам интегрирования (16) и (8) [приложение 5] получим
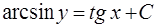 .
.
Тогда общее решение дифференциального уравнения будет иметь вид
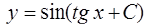 .
.
Задача 68. Найти общее решение дифференциального уравнения
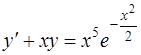 .
.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям первого порядка вида
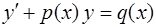 .
.
Такое уравнение можно решать методом Бернулли с помощью подстановки
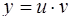 ,
,
где u(x) и v(x) – две неизвестные функции. Подставляя в исходное уравнение
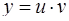 и
и 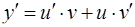 ,
,
получим
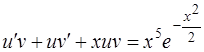 , или
, или 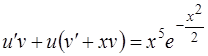 .
.
Так как одна из неизвестных функций может быть выбрана произвольно (поскольку лишь произведение uv должно удовлетворять исходному уравнению), возьмем в качестве v одно из частных решений уравнения
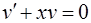 .
.
При этом исходное дифференциальное уравнение примет вид
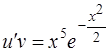 .
.
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные
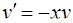 ,
,
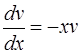 ,
, 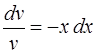 .
.
Интегрируя, находим
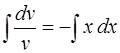 ,
,
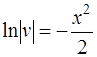 , или
, или 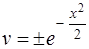
(формулы интегрирования (3), (2) [приложение 5]).
Взяв в качестве 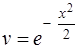 , преобразуем уравнение
, преобразуем уравнение 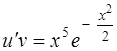 :
:
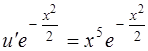 , откуда
, откуда 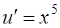 .
.
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и
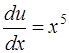 ,
, 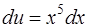 ,
,
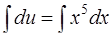 ,
, 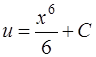
(формулы интегрирования (1), (2) [приложение 5]).
Возвращаясь к функции у, получим общее решение исходного дифференциального уравнения
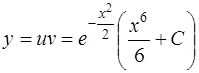 .
.
Задача 69. Найти общий интеграл дифференциального уравнения
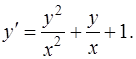
Решение. Данное уравнение относится к однородным дифференциальным уравнениям первого порядка вида 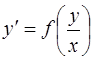 и решается заменой
и решается заменой 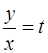 (здесь
(здесь  – новая функция), приводящей его к уравнению с разделяющимися переменными. Выполняя замену, получим
– новая функция), приводящей его к уравнению с разделяющимися переменными. Выполняя замену, получим
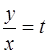 ,
, 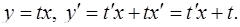
Исходное уравнение примет вид
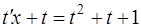 ,
,
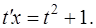
Разделяем переменные и интегрируем
 ,
, 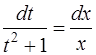 ,
,
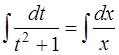 .
.
Согласно формулам интегрирования (15), (3) [приложение 5] имеем
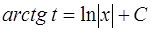 ,
,
Выполнив обратную замену, получаем решение исходного уравнения, записанное в неявном виде, то есть общий интеграл дифференциального уравнения
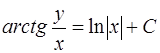 .
.
Задача 70. Найти общее решение уравнения 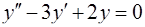 .
.
Решение. Данное дифференциальное уравнение относится к однородным линейным дифференциальным уравнениям второго порядка с постоянными коэффициентами
 .
.
Этому уравнению соответствует так называемое характеристическое уравнение
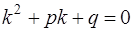 ,
,
от корней k1 и k2 которого зависит вид общего решения исходного дифференциального уравнения. При этом
1) если k1 и k2 – действительны и различны (дискриминант D > 0, 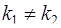 ), общее решение дифференциального уравнения имеет вид
), общее решение дифференциального уравнения имеет вид
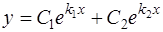 ,
,
то есть каждому корню 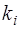 соответствует слагаемое вида
соответствует слагаемое вида 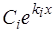 ;
;
2) если k1 и k2 – действительные и равные (дискриминант D = 0, k1 = k2 = k), общее решение дифференциального уравнения имеет вид
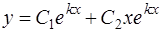 , или
, или 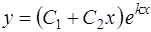 ;
;
3) если k1 и k2 – комплексные (дискриминант D < 0, 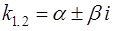 ) общее решение дифференциального уравнения в этом случае будет иметь вид
) общее решение дифференциального уравнения в этом случае будет иметь вид
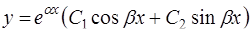 .
.
Составляя характеристическое уравнение для заданного дифференциального уравнения 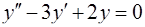 , получим
, получим
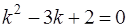 .
.
Оно имеет два различных действительных корня k1 = 1 и k2 = 2 (случай 1). Поэтому общее решение будет записано в виде
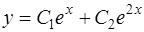 .
.
Задача 71. Найти общее решение уравнения 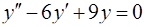 .
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
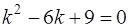 .
.
Оно имеет два равных корня k1 = k2 = 3 (случай 2). Поэтому общее решение есть
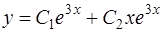 , или
, или 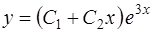 .
.
Задача 72. Найти общее решение уравнения 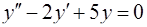 .
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
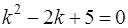 .
.
Дискриминант этого уравнения отрицательный (случай 3)
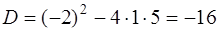 .
.
Это означает, что уравнение имеет комплексные корни
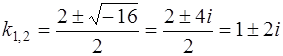 ,
,
где  – мнимая единица, такая, что
– мнимая единица, такая, что 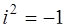 .
.
Так как 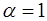 ,
, 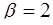 , общим решением будет
, общим решением будет
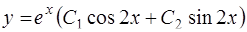 .
.
Задача 73. Найти общее решение уравнения 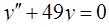 .
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
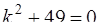 ,
,
откуда получаем: 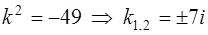 (корни комплексные – случай 3). Здесь
(корни комплексные – случай 3). Здесь 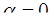 ,
,  , значит, общее решение имеет вид
, значит, общее решение имеет вид
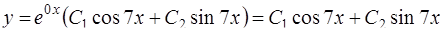 .
.
Задача 74. Найти общее решение дифференциального уравнения
 .
.
Решение. Данное уравнение является линейным однородным дифференциальным уравнением третьего порядка с постоянными коэффициентами и решается аналогично уравнениям второго порядка (см. задачу 70). Его характеристическое уравнение
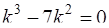 , или
, или
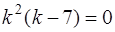 , откуда
, откуда
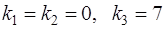 .
.
Паре корней 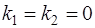 соответствует решение
соответствует решение
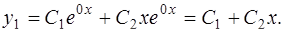
Корню 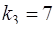 соответствует решение
соответствует решение
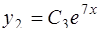 .
.
Общее решение исходного уравнения есть сумма полученных решений
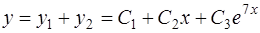 .
.
Задача 75. Найти частное решение дифференциального уравнения 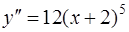 , удовлетворяющее условиям:
, удовлетворяющее условиям: 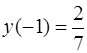 ,
, 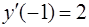 .
.
Решение. Дифференциальное уравнение вида

решается n–кратным последовательным интегрированием:
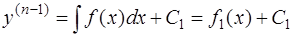 ,
,
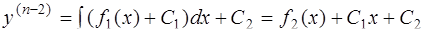 и т.д.
и т.д.
В данном случае 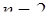 , поэтому интегрируем два раза. При этом получим (формула интегрирования (2) [приложение 5])
, поэтому интегрируем два раза. При этом получим (формула интегрирования (2) [приложение 5])
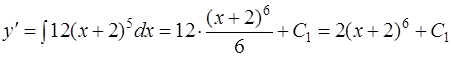 .
.
Подставив начальное условие 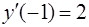 , найдем константу С1:
, найдем константу С1:
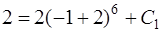 ,
, 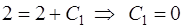 .
.
Тогда уравнение примет вид
 .
.
Еще раз проинтегрируем:
 .
.
Подставив начальное условие 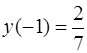 , найдем константу С2:
, найдем константу С2:
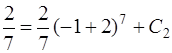 ,
, 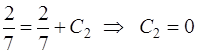 .
.
Значит, частное решение исходного дифференциального уравнения имеет вид
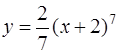 .
.
Задача 76. Найти частное решение уравнения  , удовлетворяющее условиям:
, удовлетворяющее условиям: 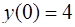 ,
, 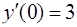 .
.
Решение. Данное дифференциальное уравнение решается аналогично задаче 75. Проинтегрировав первый раз, получим

(формула интегрирования (4) [приложение 5]).
Подставив начальное условие 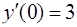 , найдем константу С1
, найдем константу С1
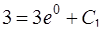 ,
, 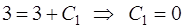 .
.
Уравнение примет вид
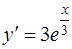 .
.
Еще раз проинтегрируем, получим
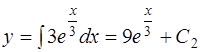 .
.
Подставив начальное условие 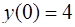 , найдем константу
, найдем константу 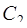 :
:
 ,
, 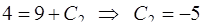 .
.
Итак, частное решение дифференциального уравнения имеет вид
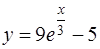 .
.
ГЛАВА 3
Дата: 2019-03-05, просмотров: 275.