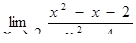Начала математического анализа»
| № |
Задания
Варианты ответов
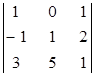
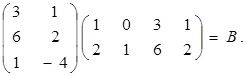 Найти сумму элементов третьего столбца матрицы В.
Найти сумму элементов третьего столбца матрицы В.
 .
.
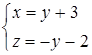
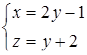
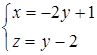

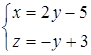
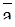 и
и 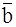 образуют угол
образуют угол 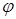 . Зная, что
. Зная, что 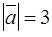 ,
, 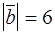 ,
, 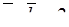 , найти
, найти 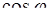 .
.
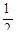
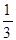
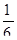
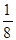
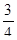
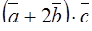 , если
, если 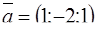 ,
, 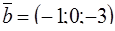 ,
, 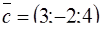 .
.
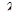 , при котором ортогональны векторы
, при котором ортогональны векторы 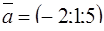 и
и 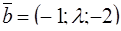 .
.
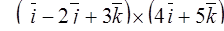
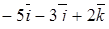

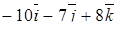
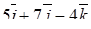
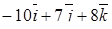
| 8. | Векторы 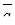 и и 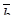 образуют угол образуют угол 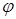 = = 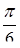 . Зная, что . Зная, что 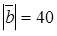 , , 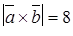 , найти , найти 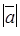 . .
| 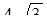
| 2 | 4 | 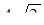
| 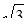
|
| 9. | Если плоскость 3x - By +6z -1=0 параллельна плоскости С x +10y +4z +7=0, то B + C = | 10 | -13 | 13 | 5 | -9 |
| 10. | Составить уравнение плоскости, проходящей через точку М(-1; 4; 5) перпендикулярно прямой 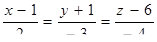
| 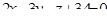
| 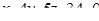
| 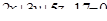
| 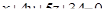
| 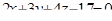
|
| 11. | Уравнение прямой, проходящей через точки А(2; -3; 5) и В(0; 4; -7), имеет вид | 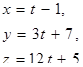
| 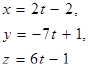
| 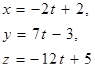
| 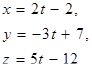
| 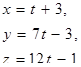
|
| 12. | Уравнение прямой, проходящей через точку
М(2; 4; -5) параллельно прямой 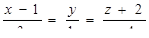
| 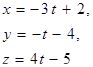
| 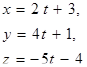
| 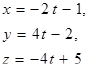
| 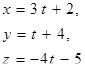
| 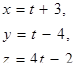
|
| 13. | Прямые  и и 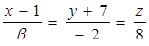 параллельны. Найти параллельны. Найти 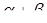 . .
| 18 | 9 | -9 | 5 | -18 |
| 14. | Определить, при каком 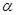 перпендикулярны прямые перпендикулярны прямые 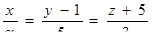 , , 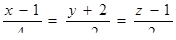 . .
| -1 | 1 | 2 | 3 | 5 |
| 15. | Вычислить 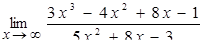
| 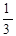
| 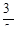
| 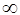
| 0 | 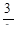
|
| 16. | Вычислить | 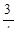
| 0 | 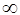
| 1 | 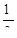
| |
| 17. | Вычислить 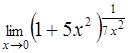
| 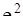
| 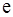
| 1 | 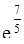
| 
| |
| 18. | Вычислить 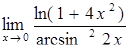
| 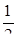
| 0 | 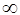
| 2 | 1 | |
| 19. | Вычислить 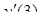 , если , если 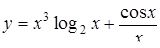
| 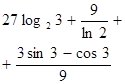
| 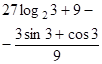
| 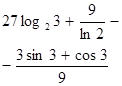
| 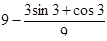
| 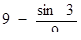
| |
| 20. | Для функции 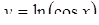 найти найти 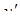
| 
| 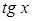
| 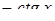
| 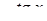
| 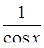
| |
| 21. | Для функции 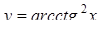 найти найти 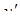 . .
| 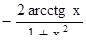
| 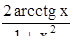
| 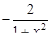
| 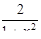
| 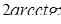
| |
| 22. | Найти интервалы убывания функции 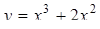
| 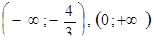
| 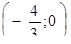
| 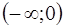
| 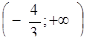
| 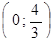
| |
| 23. | Найти интервалы вогнутости функции 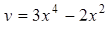
| 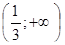
| 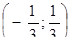
| 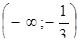
| 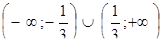
| 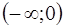
| |
Правильные ответы
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Ответ | 1 | 2 | 4 | 3 | 1 | 2 | 5 | 3 | 2 | 1 | 3 | 4 | 5 | 2 | 3 | 1 | 5 | 5 | 3 | 4 | 1 | 2 | 4 |
Приложение 2
Тренировочный тест к разделу « Интегралы, ряды, дифференциальные уравнения »
| № | |||
Задания
Варианты ответов
1
2
3
4
5
1.
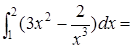
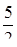
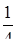


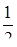
2.
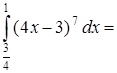
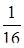
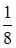
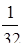
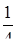
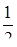
3.
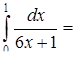
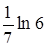
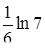
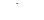
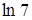
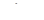
4.
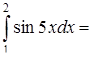
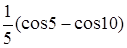
cos 5–cos 10
5(cos 5–cos 10)
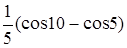
5(cos 10–cos 5)
5.
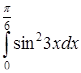 =
=
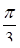
1
0
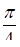
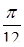
6.
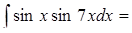
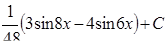
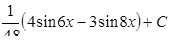
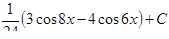
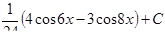
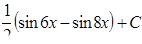
7.
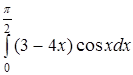 =
=
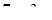

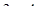
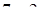
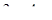
8.
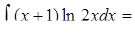
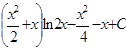
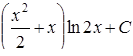
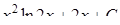
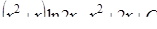
9.
Найти площадь области D,
ограниченной линиями: 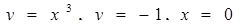 .
.
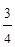
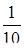
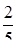
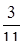
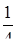
10.
Найти площадь области D,
ограниченной линиями: 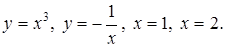
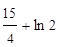
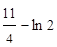
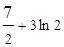
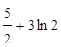
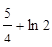
11.
Найти общее решение дифференциального уравнения
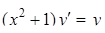 .
.

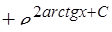
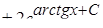
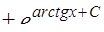

12.
Найти общее решение дифференциального уравнения
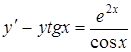 .
.
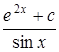
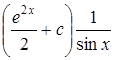
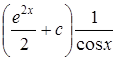
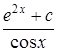
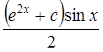
13.
Найти общий интеграл дифференциального уравнения
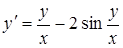 .
.

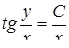
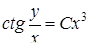
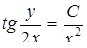
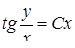
14.
Найти общее решение дифференциального уравнения
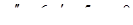
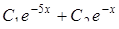
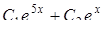
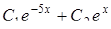

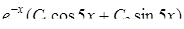
15.
Найти общее решение дифференциального уравнения
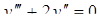
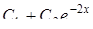
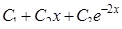
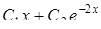
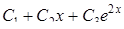

| 16. | Найти общее решение дифференциального уравнения 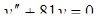
| 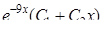
| 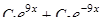
| 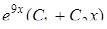
| 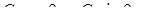
| 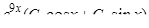
|
| 17. | Найти частное решение дифференциального уравнения 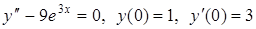
| 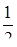 e3x e3x
| 3e3x | 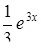
| e3x | 2e3x |
| 18. | Определить, какие ряды сходятся:
А) 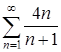 ; Б) ; Б) 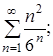 В) В) 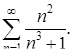
| А, Б | Б, В | Б | А, В | В |
| 19. | Определить, какие ряды сходятся:
А) 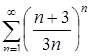 ; Б) ; Б) 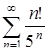 ; В) ; В) 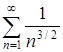 . .
| А, Б | А | Б, В | В | А, В |
| 20. | Исследовать на сходимость ряды:
А) 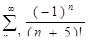 ; Б) ; Б) 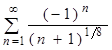 . .
| Оба сх. абсолютно | А сх.условно; Б сх.абсолютно | А сх.абсолютно; Б сх.условно | Оба расходятся | Оба сходятся условно |
| 21. | Найти область сходимости функционального ряда 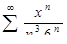 . .
| (-6;6) | [-6;6) | [0;6] | (-6;6] | [-6;6] |
Правильные ответы
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Ответ | 4 | 3 | 2 | 1 | 5 | 2 | 4 | 1 | 1 | 1 | 4 | 3 | 4 | 1 | 2 | 4 | 4 | 3 | 5 | 3 | 5 |
Приложение 3
Тренировочный тест к разделу « Теория функций комплексной переменной,
Операционное исчисление, теория вероятностей »
| № |
Задания
Варианты ответов
2
3
4
5
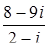

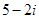


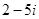
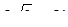
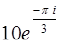
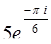
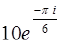
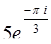
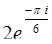
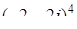
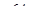
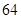
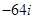

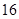

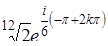 ,
, 
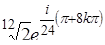 ,
,
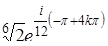 ,
,
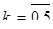
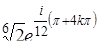 ,
,
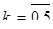
 ,
,
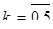
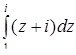
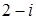
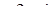
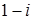
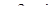
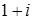
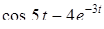
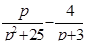
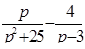
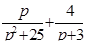
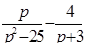
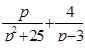
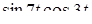
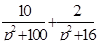
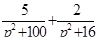
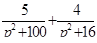
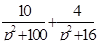
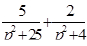
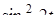
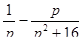
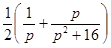
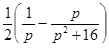
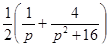
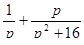
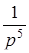
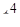
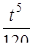
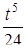
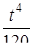
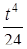
Найти оригинал для изображения 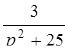
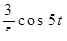
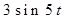

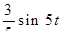

Найти изображение свертки функции 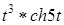
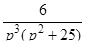
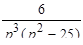
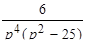
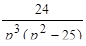
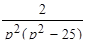
Решить дифференциальное уравнение
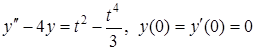
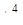
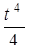
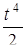
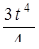
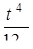
Устройство содержит 4 независимо работающих элемента с вероятностями отказа 0,9; 0,4; 0,2; 0,5. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
0,976
0,024
0,964
0,97
0,98
Из 10 стрелков 5 попадают в цель с вероятностью 0,4; 2 – с вероятностью 0,8; 3 – с вероятностью 0,6. Найти вероятность того, что наудачу выбранный стрелок попадет в цель.
0,48
0,18
0,54
0,64
0,72
Дискретная случайная величина Х задана законом распределения. Найти D ( X ), если М(Х) = 2,9.
| Х | х1 | 5 |
| р | 0,7 | р2 |
18,9
2,89
0,89
1,09
1,89
Дискретная случайная величина задана рядом распределения. Найти D ( X ).
| Х | 1 | 3 | 5 |
| р | р1 | 0,3 | 0,2 |
6,76
4,28
3,75
5,12
2,44
Дискретная случайная величина Х задана рядом распределения. Найти 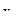 , если М(Х) = 1,7.
, если М(Х) = 1,7.
| Х | 1 | 2 | х3 |
| р | р1 | 0,1 | 0,2 |
1
4
3
5
2
Задана плотность распределения непрерывной случайной
величины Х: 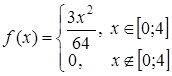 . Найти
. Найти 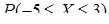 .
.
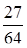
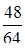
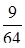
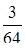
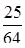
Задана плотность распределения непрерывной случайной
величины Х: 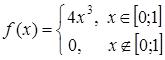 . Найти М(Х).
. Найти М(Х).
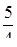
1
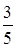
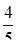
Найти дисперсию случайной величины Х – числа появлений события А в 18 независимых испытаниях, если вероятности появления события в каждом испытании одинаковы, а М(Х) = 8.
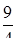
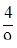

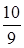
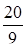
Случайная величина Х – число появлений события А в n испытаниях распределена по биномиальному закону с М(Х) = 10, D(X) = 7. Найти вероятность появления события А в каждом испытании.
0,3
0,2
0,35
0,4
Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: М(Х) = 0,5 см, D(X) =0,36 см2. Деталь считается годной, если ее диаметр не менее 0,464 и не более 0,536 см. Определить, какой процент деталей будет забракован.
4,78%
95,22%
97,61%
2,39%
Дальность полета снаряда распределена нормально с математическим ожиданием 800 м и средним квадратическим отклонением 40 м. Определить интервал, в который согласно правилу 3 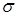 попадет снаряд с вероятностью 0,9973.
попадет снаряд с вероятностью 0,9973.
(720, 880)
(780, 820)
(760, 840)
(680, 920)
Правильные ответы
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Ответ | 2 | 3 | 1 | 5 | 4 | 1 | 2 | 3 | 5 | 4 | 2 | 5 | 1 | 3 | 5 | 5 | 2 | 1 | 4 | 3 | 1 | 2 | 4 |
Приложение 4
Таблица эквивалентности бесконечно малых
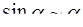
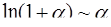
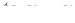
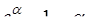
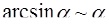
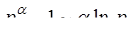
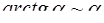
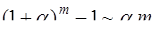
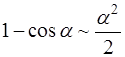 (формулы справедливы при
(формулы справедливы при 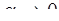 )
)
ТАБЛИЦА ПРОИЗВОДНЫХ
Дата: 2019-03-05, просмотров: 343.