Задана вентиляционная сеть произвольной сложности, а также общее количество воздуха или тип вентилятора для проветривания шахты. Необходимо определить расходы воздуха во всех ветвях соединения.

Для любого элементарного контура вентиляционной сети всегда выполняются 1-й и 2-й законы расчета вентиляционных сетей:

                                                            ∑q_i=0                                                    (7.1)

                                                              ∑h_i=0                                                    (7.2)

                                                             ∑h_i+∑p_i=0                                             (7.3)

где ∑q_i-сумма расходов воздуха в узле;

∑h_i- алгебраическая сумма депрессий ветвей элементарного контура;

∑p_i- алгебраическая сумма давлений, создаваемая вентиляторами во всех ветвях замкнутого контура.

Задача о распределении воздуха в сложной вентиляционной сети решается методом последовательных приближений. Он заключается в том, что первоначальное распределение воздуха задается произвольно, однако в целом по контуру или для узла сети оно должно подчиняться уравнению неразрывности потока, т.е. равенству (7.1).

Первоначально произвольно принятое значение расхода воздуха в ветви q_i отличается от действительного q 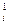 на некоторую величину ∆q_i. Тогда депрессия любой ветви h_i может быть выражена равенством:

                                      h_i=R_i q 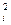= R_i (q 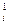+∆q_i)²                                                  (7.4)

Раскрывая скобки правой части равенства, получим

                                     h_i= R_i (q 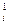)²+2 R_i q  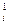∆q_i+ R_i (∆q_i)²                               (7.5)

Полагая, что ∆q_i мало, отбрасываем тем более малую величину R_i (∆q_i)² и из равенства (7.5) определяем величину ошибки для одной ветви

                                                ∆q_i= 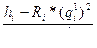                                                           (7.6)

Для всех ветвей, входящих в элементарный контур величина ошибки определится по формуле

                                               ∆q_i= 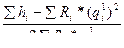                                                         (7.7)

С учетом равенства (7.3), согласно которому ∑h_i=-∑p_i , окончательно получим

                                                    ∆q_i= 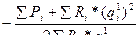                                                (7.8)

где -алгебраическая сумма депрессий ветвей замкнутого контура;

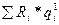 -сумма произведений R_i на q  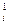по всем ветвям, взятая без учета направления потока;

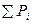-алгебраическая сумма давлений, создаваемая вентиляторами во всех ветвях замкнутого контура.

При расчете распределения воздуха в сложной вентиляционной сети необходимо выполнять следующие правила:

1. Обход каждого элементарного контура выполнять по часовой стрелке;

2. Потоки, направленные по часовой стрелке считаются положительными, против часовой стрелки отрицательными;

3. Если величина ошибки (поправки) рассчитанная по формуле (7.8) положительна (>0), то она суммируется с потоками воздуха, направление которых совпадает с направлением обхода контура и вычитается из расходов направленных против направления обхода контура;

4. Если величина ошибки имеет отрицательный знак, она вычитается из потоков воздуха, направление которых совпадает с направлением обхода контура и суммируется с противоположными потоками;

5. Если величина ошибки по абсолютному значению больше первоначально принятого расхода воздуха и вычитается из него, это значит, что первоначально принятое направление воздуха неверно и его необходимо изменить на противоположное направление.

6. Расчет выполняется несколько раз, пока последующие расходы воздуха будут отличаться от предыдущих расходов с требуемой степенью точности.

Пример расчета

Заданы сопротивления ветвей последовательно - диагонального соединения горных выработок (рис.7.1). Для проветривания сети установлен вентилятор ВОД-21, с углом установки лопаток рабочего колеса 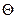=40⁰. Определить расходы воздуха в сети и во всех ветвях соединения.

Рис.7.1 Схема к расчету распределения воздуха в ветвях последовательно-диагонального соединения горных выработок

Решение задачи.

1. Определяем число независимых уравнений для решения задачи, которое равно числу независимых контуров. Между числом независимых контуров, узлов и ветвей любой схемы существует следующая зависимость

                                                       К=В-У+1,                                    (7.9)

где К- число контуров; В- число ветвей; У- число узлов.

В нашем примере К=6-4+1=3. Следовательно, используя равенство (7.9), необходимо составить три независимых уравнения. В это равенство входит алгебраическая сумма давлений, создаваемая вентилятором. В нашем примере это вентилятор ВОД-21 с углом установки лопаток рабочего колеса 40⁰. Для решения задачи необходимо аппроксимировать характеристику вентилятора. В области промышленного использования характеристика вентилятора достаточно точно описывается равенством

                                                    H=a-b*Q²,                                                    (7.10)

где а- коэффициент, имеющий размерность и смысл депрессии;

b- коэффициент, характеризующий внутреннее сопротивление вентилятора.

Возьмем две точки, расположенные на концах рабочей характеристики вентилятора ВОД-21 при =40⁰

Рис.6.17 К пояснению аппроксимации аэродинамической характеристики вентилятора ВОД-21 с углом установки лопаток рабочего колеса 40⁰

Точка 1 на графике соответствует координатам Н₁=400, кг/м² Q₁ =43 м³/с, а точка 2

Н₂=200 кг/м², Q₁ =64 м³/с. Тогда можно составить два уравнения

400=а-b 43²

200=а-b 64²

Из этих равенств определяем, а=564, b=0.089 и характеристика вентилятора опишется равенством

                                                Н=564-0.089 Q²                                       (7.11)

Обозначим контура. Контур 1-й 0-1-3-4-5-0, контур 2-й 1-2-3-1, контур 3-й 2-4-3-2.

Составим расчетные уравнения для обозначенных контуров:

Для первого контура

                               ∆q₁=- 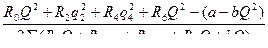                            (7.12)

После незначительных преобразований, получим для первого контура

                                      ∆q₁=- 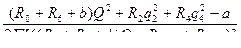                            (7.13)

В нашем примере R₀+R₆+b=0.154 кµ. Подставляя значения постоянных в равенство (6.88) получим формулу для расчета поправок в первом контуре

                         ∆q₁=- 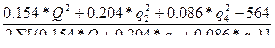                               (7.14)

Составим уравнение для расчета поправок во втором контуре

                                      ∆q₂= 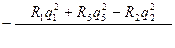                                   (7.15)

Подставляя значения сопротивлений в равенство (7.15), получим

                  ∆q₂= 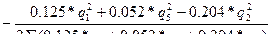                                     (7.16)

Составим уравнение для расчета поправок в третьем контуре

                                            ∆q₃= 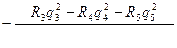                                (7.17)

После подстановки значений аэродинамического сопротивления ветвей, получим

                             ∆q₃= 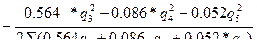                             (7.18)

Принимаем первоначальное, произвольное распределение воздуха:

Q=45м³/с; q₁₌25 м³/с; q₂=20 м³/с; q₃₌15 м³/с; q₄=30 м³/с; q₅=10 м³/с;

По формуле (7.14) определяем величину ошибки для первого контура. В нашем примере она будет равна 3.4 м³/с. Исправляем первоначально принятые значения воздуха в первом контуре

Q=48.4 м³/с, q₂=23.4 м³/с; q₄ 33.4 м³/с;

По формуле (7.16) определяем величину ошибки для второго контура. В результате расчета получим ∆q₂=3.3 м³/с. Исправляем первоначально принятые значения расходов воздуха во втором контуре

q₁=28.3 м³/с, q₅=13,3 м³/с, q₂=20,1 м³/с.

По формуле (7.18) определяем величину ошибки для третьего контура. В результате расчета получим ∆q₃=-1.8 м³/с. Исправляем первоначально принятые значения воздуха

q₃=13,2 м³/с, q₄=35,2 м³/с, q₅=15,1 м³/с.

Далее, снова выполняем расчет величины ошибки для всех контуров и исправляем расходы воздуха. Расчет повторяется несколько раз, пока последующие расходы воздуха будут отличаться от предыдущих расходов с требуемой степенью точности.

Результаты расчетов сводим в табл. 7.1.