Рис.6.7. Последовательное соединение горных выработок

В соответствии с первым законом расчета вентиляционных сетей поток воздуха, приходящий в точку соединения двух любых соседних ветвей должен быть равен потоку, уходящему из этой точки, т.е.

                                    q₁=q₂=   q_i=  q_n=Q                                 (6.13)

Депрессия любой выработки, входящей в последовательное соединение есть разность давлений между ее началом и концом, т. е.

                                                     h_i=P_i-P_i-1                                          (6.14)

Тогда логично разность давлений в начальной и конечной точках всего соединения определить, как общую депрессию соединения т. е.

                                                    H=P₀-P_n                                                (6.15)

Сложим депрессии всех ветвей последовательного соединения

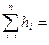             (P₀-P₁)+(P₁-P₂)+ +(P_i-1-P_i)+ (P_n-1-P_n)                (6.16)

В равенстве (6.16) каждому слагаемому кроме Р₀ и Р_n найдется равное слагаемое с противоположным знаком, поэтому

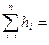                                             P₀ - P_n                                            (6.17)

и с учетом равенства (6.15)

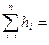                                              Н                                            (6.18)

Общая депрессия последовательного соединения равна сумме депрессий всех ветвей, входящих в соединение

Разделим обе части равенства (6.18) на квадрат расхода воздуха q =Q²

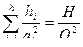                                                                                              (6.19)

В соответствии с равенством (6.11) 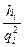 =R_i ,следовательно, можно записать

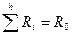                                                                                              (6.20)

То есть общее сопротивление последовательного соединения равно сумме сопротивлений ветвей, входящих в соединение

Депрессия любой ветви последовательного соединения, как и депрессию всего соединения можно выразить через аэродинамическое сопротивление и расход воздуха т. е.

                                                  h_i=R_i q                                             (6.21)

                                                   H=R₀ Q²                                            (6.22)

Из равенств (6.21) ,(6.22) q =h_i /R_i , и Q² =H/R₀ , а так как в последовательном соединении q_i=Q то можно записать

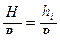                                                                                                      (6.23)

Из равенства (6.23) следует

                                                    h_i = 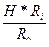                                        (4.24)

В последовательном соединении депрессии отдельных ветвей пропорциональны их сопротивлениям.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ И ЕГО СВОЙСТВА

Параллельное соединение горных выработок может быть простым (рис.6.8) и сложным (рис.6.9).

Простым параллельным называется такое соединение вентиляционных ветвей, в котором все начала ветвей расходятся в одном узле, а сходятся в другом (рис.6.8).

Сложным параллельным соединением называется такое соединение, когда кроме параллельных ветвей расходящихся в одном узле и сходящимся в другом в этих ветвях имеются дополнительные параллельные ветви (рис.6.9).

Рассмотрим свойства простого параллельного соединения. Согласно определению депрессии разность давления в узлах 1, 2 определяет как депрессию любой ветви входящей в соединение, так и депрессию всего соединения, тогда можно записать

                       Р₁-Р₂=h₁=h₂₌ =h_i= h_n=H                                  (6.25)