Выпускаются два типа вентиляторов, различающихся по конструктивному исполнению и принципу действия - центробежные и осевые.
Центробежные вентиляторы отличаются более высоким напором при меньшей производительности, а осевые наоборот, более высокой производительностью при меньшем напоре.
Существуют понятия полной характеристики вентилятора и области его промышленного использования, т.е. той его части, где вентилятор работает устойчиво, а его К.П.Д. не ниже 0.6.(рис.8.1)
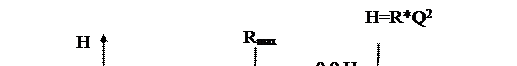
Рис.8.1 Аэродинамическая характеристика вентилятора и режим его работы на вентиляционную сеть
В верхней части характеристики вентилятора область промышленного использования ограничена линией проходящей через точки, где напор вентилятора составляет 0.9 от максимального напора развиваемого вентилятором. В нижней части линией проходящей через точки, где к.п.д. вентилятора составляет 0.6. С права максимальным, а слева минимальным углом установки лопаток рабочего колеса или направляющего аппарата.
Режим работы одного вентилятора на сеть, который определяется его производительностью и депрессией (Q, H), можно определить аналитическим и графическим методом.
Сущность аналитического метода состоит в замене графической характеристики вентилятора подходящим математическим выражением Н(Q), график которого был бы близок к характеристике вентилятора, по крайней мере, в области его промышленного использования. Наибольшее распространение получило уравнение вида
Н=a - bQ2 (8.1)
где «a » и «b »-числовые параметры, определяемые по графической характеристике вентилятора.
Для этого на рабочей ветви характеристики (лучше всего на концах выбранного участка характеристики) выбираются две точки, например 1, 2 (см. рис.8.1). Параметры приближенной характеристики вентилятора определяют из условий прохождения ее через обе выбранные точки, для чего выписывают координаты этих точек, снимаемые с графика: Q1, H1, Q2, H2. Затем составляют два уравнения
H1=a-b*Q 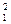 (8.2)
(8.2)
H2=a-b*Q 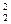 (8.3)
(8.3)
Эти уравнения линейны относительно неизвестных «a» и «b». Так как коэффициенты при неизвестном «а» в обоих уравнениях одинаковы, наиболее простой способ решения системы уравнений (8.2), (8.3) состоит в вычитании из первого уравнения второго. При этом исключается неизвестное «а» и получается простейшее уравнение относительно «b»
b= 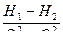 (8.4)
(8.4)
Подстановкой найденного значения «b» в любое из уравнений (8.2), (8.3) можно определить параметр «а».
Зависимость депрессии от расхода воздуха для любой вентиляционной сети, выражается уравнением
Н=R Q2 , (8.5)
которое является уравнением характеристики вентиляционной сети.
где R-аэродинамическое сопротивление вентиляционной сети.
Приравняв правые части равенств (8.1), (8.5), найдем расчетную производительность вентилятора, или расход воздуха в сети:
Q= 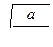 (8.6)
(8.6)
Подставив это выражение в уравнение (8.5) определим расчетное значение депрессии
Н= 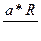 (8.7)
(8.7)
Графический метод определения режима работы вентилятора заключается в графическом построении на одном чертеже в одном масштабе характеристики вентилятора, которая берется из справочных источников, и характеристики сети, которая строится по уравнению (8.5). Координаты точки пересечения характеристики вентилятора и вентиляционной сети (например, точка «с») определяют искомые величины Q и Н. Очевидно, что при работе одного вентилятора на вентиляционную сеть его производительность и напор должны удовлетворять как собственной характеристике, так и характеристике сети, т.е. графически определяться точкой пересечения характеристики вентилятора и сети.
Следовательно, любой вентилятор может работать на сеть устойчиво и с к.п.д. не ниже 0.6, сопротивление которой находится в пределах Rmin ≤ R ≤ Rmax (см. рис.8.1). При работе вентилятора на любую сеть с сопротивлением R его производительность может изменяться только в определенных пределах от Qmin до Qmax.
Дата: 2019-03-05, просмотров: 372.