Для этой цели используются приемники давления, измерители и линии связи (трубки). В качестве приемников давления используются воздухомерные трубки различной конструкции. Наиболее распространенной из них является трубка Пито-Прандля, схема которой представлена на рис.5.3
В этой трубке приемником статического давления служит кольцевая щель или 4-6 отверстий 1 диаметром 0.1d , расположенных по периметру трубки, а приемником полного напора - осевое отверстие 2.
 | |||
| |||
Рис.5.3 Схема воздухомерной трубки
Измерителями давления служат жидкостные манометры и микроманометры. В рудничной вентиляции широкое распространение получили микроманометры типа ММН, схема которого представлена на рис.5.4
Рис.5.4 Схема микроманометра
Жидкостный микроманометр, изображенный на рис.5.4, состоит из двух колен, одно из которых имеет изменяемый в определенных пределах наклон и значительно меньший диаметр. Как видно из рисунка 2.4, к широкому сосуду подведено большее давление, а меньшее - к подвижной измерительной трубке малого диаметра.
Обозначим площадь измерительной трубки f , а поперечное сечение сосуда - через F. Под действием разности давлений ∆Р=Р1-Р2 =hγж (где Р1> Р2 и γж- удельный вес жидкости) уровень жидкости в трубке повысится на величину «а» от нулевого положения, а в широком сосуде – опустится на величину h0 от начального нулевого положения, при этом объем жидкости равный h0 F, перетечет в трубку и будет равен объему а f, т.е.
h0 F= а f (5.9)
Разность уровней в коленах будет равна
h=h0 + h1 (5.10)
где h0-вертикальная высота опускания жидкости в широком сосуде;
h1-вертикальная высота подъема жидкости в измерительной трубке.
Но h1=а Sinα (5.11)
и h0=а f / F (5.12)
Подставив вместо h1 и h0 их значения в предыдущее уравнение, получим
h=a (Sinα +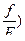 
(5.13)
Следовательно, искомая разность давлений
∆Р= γж h=a (Sinα + 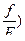γж (5.14)
Отсюда видно, что увеличение «масштаба» измерения есть отношение отсчитываемой на шкале прибора величины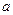 
к вертикальной высоте столба жидкости, h уравновешивающей измеряемую разность давлений,
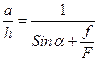(5.15)
Чувствительность прибора будет тем больше, чем меньше отношение f/F и чем меньше угол наклона α. В микроманометрах типа ММН-240 f/F=1/400, Sinα=0,2-0,8, а диаметр трубки 2 мм.
ОСНОВНЫЕ ЗАКОНЫ АЭРОДИНАМИКИ
Движение воздуха в шахте подчиняется законам сохранения массы и энергии
Закон сохранения массы
. Закон сохранения массы применительно к движению воздуха формулируется следующим образом: масса любого объема воздуха остается постоянной в процессе его движения.
Если в потоке выделить элементарный объем ω, достаточно малый, чтобы плотность воздуха в нем можно было считать постоянной, то закон сохранения массы можно записать так:
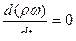(5.16)
где ρω – масса выделенного объема
Через проекции скорости потока в рассматриваемой точке на оси координат этот закон запишется так:
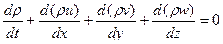(5.17)
где u, v,w- соответственно, проекции скорости в рассматриваемой точке потока на оси x, y, z системы координат.
Для стационарного движения плотность, скорость, давление, температура в фиксированной точке потока не изменяются, тогда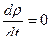 
и равенство (5.17) запишется так
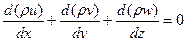, (5.18)
а при постоянной плотности потока ρ=const
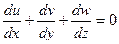(5.19)
В выработке постоянного сечения v=w=0 тогда из уравнения (5.19) найдем, что u=const, т. е. скорости движения воздуха в сходственных точках постоянны. Из уравнения (5.19) также следует, что увеличение скорости в одном направлении должно вызывать уменьшение ее в другом направлении, так как сумма членов в его левой части будет равна нулю тогда, когда одни из них будут положительны (ускорение течения), другие отрицательными (замедление).
Для случая стационарного движения воздуха в выработке из уравнения (5.16) получим
М=const (5.20)
Выразим массовый расход воздуха в выработке в виде
М=ρ*Q (5.21)
где Q-объемный расход воздуха в выработке.
Тогда для изотермического процесса (т.е. при ρ=const) из выражения (5.21) получим
Q=const (5.22)
Из выражения (5.22), называемого уравнением расхода, следует, что для стационарного движения объемный расход воздуха в выработке постоянный.
При разветвлении потока уравнение (5.22) примет вид
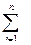Qi=0 (5.23)
где i – номер потока; n – число потоков в разветвлении.
Закон сохранения энергии
Закон сохранения энергии, является основным законом движения воздуха по горным выработкам. При выводе основного закона принимают, что его объемный вес остается постоянным, т. е. рассматривают воздух как несжимаемый. Это ведет к погрешности, которая не более 7-10 %.
Рис.5.5 Схема к выводу уравнения Бернулли для струйки воздуха в выработке
В элементарной струйке тока выделим объем, а b с d (рис.5.5). Элементарная струйка тока это струйка настолько малого поперечного сечения, что скорость движения воздуха в любом ее сечении постоянна. Элементарная струйка тока ограничена линиями тока. Линия тока это геометрическое место точек, касательная в любой точке есть вектор скорости потока. Через некоторое время dt объем переместится и займет положение a1b1c1d1. Площадь поперечного сечения струйки в ab S1, в cd S2, давление соответственно Р1, Р2. В предположении не сжимаемости потока воздуха перемещение объема воздуха a b c d в положение a1b1c1d1 можно рассматривать как перемещение объема воздуха abb1a1 в положение cd d1c1 при неизменном положении объема a1b1cd. Принимая во внимание закон сохранения энергии, запишем, что приращение кинетической энергии указанного объема равно работе внешних сил, т.е.
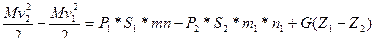, (5.24)
где М и G – соответственно масса и вес элементарного объема воздуха. В равенстве (5.24) S1*mn=V1, а S2*m1n1=V2 и V1=V2=V-объем воздуха.
V=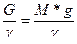 
(5.25)
С учетом равенства (5.25) будем иметь
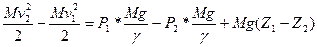, (5.26)
Сгруппировав члены с однородными индексами, получим уравнение Бернулли для идеальных жидкостей и газов
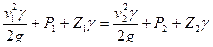(5.27)
В действительности при движении воздуха по выработкам имеет место трение его о стенки выработок. Обозначим потерю давления на трение через h. Кроме этого необходимо учесть, что в процессе движения воздуха по выработкам изменяется его объемный вес, т. е. γ ≠ const. Тогда равенство (5.27) запишется в виде
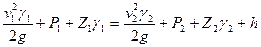(5.28)
Из равенства (5.28) следует, что разность давлений, расходуемая на преодоление сопротивления сети горных выработок, определяется по формуле
h=(P1-P2)+(Z1 γ1-Z2 γ2)+(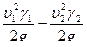 
) (5.29)
Равенство (5.29) является общим выражением закона движения воздуха по горным выработкам.
В этом равенстве (P1-P2)-разность давлений, создаваемая вентилятором;
(Z1 γ1-Z2γ2)-разность весов столбов воздуха, которая называется естественной тягой;
( 
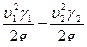)-скоростной напор;
Тогда получим
h=hв±hе±hск (5.30)
Из равенства (5.30)следует, что разность давлений, расходуемая вентилятором на преодоление сопротивления сети горных выработок движущимся по ним воздухом, слагается из перепада давления, создаваемого вентилятором, естественной тягой и скоростным напором. Причем в общем случае естественная тяга может способствовать или противодействовать работе вентилятора, входное и выходное сечение потока могут отличаться по величине, что учитывается знаком перед hе и hск
Дата: 2019-03-05, просмотров: 328.
