В зависимости от динамического действия на фундамент машины разделяют на две группы, а в каждой группе на две подгруппы:
| Группы машин | Вид главного движения машины | Наименование машины |
| Периодического действия | Равномерное вращение | Электрические машины, турбоагрегаты |
| Равномерное вращение и связанное с ним возвратно-поступательное движение | Машины с кривошипно-шатунными механизмами | |
| Непрерывного действия | Неравномерное вращение или возвратно-поступательное движение | Приводные электродвигатели прокатных станов |
| Возвратно-поступательное движение, завершаемое ударом | Молоты, копры |
Расчетное сопротивление грунта в основании фундамента, испытывающего динамические нагрузки, определяется по формуле:
Rd = a×R ,
где R – расчетное сопротивление грунта для фундамента, не испытующего динамические нагрузки (см. лекцию 1); a - понижающий коэффициент, принимаемый в зависимости от вида динамического воздействия:
| Вид динамического воздействия | График динамического воздействия | Значе-ние a | ||||||
  Неуравновешенные центробежные силы инерции машин с равномерно вращающимся ротором Неуравновешенные центробежные силы инерции машин с равномерно вращающимся ротором
|

| 0,8 | ||||||
   Машины с кривошипно-шатунными механизмами Машины с кривошипно-шатунными механизмами
|
| 1,0 | ||||||
   Машины, движущиеся части которых совершают неравномерные вращения и передают моменты Машины, движущиеся части которых совершают неравномерные вращения и передают моменты
|
| 1,0 | ||||||
  Импульсные машины ударного действия Импульсные машины ударного действия
|

| 0,4 |
Жесткостные характеристики грунтового основания определяются коэффициентами упругости, впервые введенными Д. Барканом:
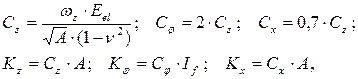 (8.1)
(8.1)
где A и If – соответственно площадь подошвы и момент инерции площади подошвы фундамента относительно центральной оси, вокруг которой осуществляется поворот; w z – коэффициент формы подошвы фундамента; Eel, n - модуль упругости и коэффициент Пуассона грунта основания;
Cz, C j, Cx – коэффициенты упругости основания соответственно при равномерном сжатии, неравномерном сжатии и равномерном сдвиге (кН/м3); Kz, K j, Kx – приведенные коэффициенты упругости основания соответственно при равномерном сжатии, неравномерном сжатии и равномерном сдвиге.
При неоднородном по глубине основании деформационные характеристики грунта Eel и n осредняются по глубине сжимаемой толщи.
 Расчет фундаментов на динамические нагрузки периодического действия. Расчетная схема фундамента представляет собой абсолютно жесткий штамп (рис. 8.1) на упругом основании, деформационные свойства которого определяются коэффициентами упругости по формуле (8.1). На фундамент действует вертикальная статическая нагрузка Q, приложенная в центре тяжести и равная весу машины, фундамента и грунта на его свесах. При работе машины фундамент испытывает вертикальную динамическую нагрузку P×sin w t, где Р – амплитуда динамической нагрузки (кН); t – время (с); w = 2×p / T (рад/с) - круговая частота; Т – период колебаний (с). Сведения о параметрах динамических нагрузок содержатся в техническом паспорте на машину. От действия статических нагрузок фундамент получает осадку s. Действие динамической нагрузки вызывает осадку фундамента z(t), являющуюся функцией времени. Вертикальные нагрузки, действующие на фундамент, уравновешиваются отпором грунта, равным произведению осадок фундамента на коэффициент упругости при равномерном сжатии Kz.
Расчет фундаментов на динамические нагрузки периодического действия. Расчетная схема фундамента представляет собой абсолютно жесткий штамп (рис. 8.1) на упругом основании, деформационные свойства которого определяются коэффициентами упругости по формуле (8.1). На фундамент действует вертикальная статическая нагрузка Q, приложенная в центре тяжести и равная весу машины, фундамента и грунта на его свесах. При работе машины фундамент испытывает вертикальную динамическую нагрузку P×sin w t, где Р – амплитуда динамической нагрузки (кН); t – время (с); w = 2×p / T (рад/с) - круговая частота; Т – период колебаний (с). Сведения о параметрах динамических нагрузок содержатся в техническом паспорте на машину. От действия статических нагрузок фундамент получает осадку s. Действие динамической нагрузки вызывает осадку фундамента z(t), являющуюся функцией времени. Вертикальные нагрузки, действующие на фундамент, уравновешиваются отпором грунта, равным произведению осадок фундамента на коэффициент упругости при равномерном сжатии Kz.
Уравнение равновесия проекций на вертикальную ось всех сил, действующих на фундамент в момент времени t, имеет вид:
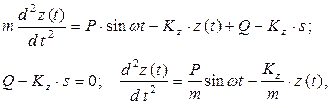 (8.2)
(8.2)
где m – масса машины, фундамента и грунта на его свесах, приведенная к центру тяжести фундамента.
Преобразуем уравнение (8.2), полагая для упрощения записей z(t) º z:
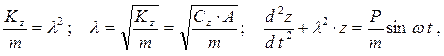 (8.3)
(8.3)
где l - частота собственных колебаний фундамента с машиной и грунтом на его свесах (1/с); w - частота вынужденных колебаний, сообщаемых фундаменту при работе машины (рад/с).
Частное решение уравнения (8.3) принимаем в виде: z = Z0×sin w × t. Амплитуду колебаний Z0 определяем подстановкой в уравнение (8.3) его частного решения:
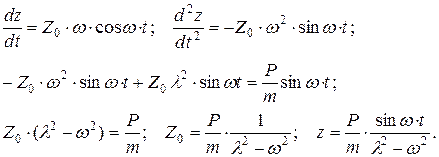 (8.4)
(8.4)
Из полученного решения следует, что при w » l наступает явление резонанса и динамическая осадка фундамента z стремится к бесконечности. В нормах на проектирование фундаментов с динамическими нагрузками амплитуда колебаний фундамента ограничивается величинами 0,15–0,25 мм. Для анализа влияния конструктивных параметров фундамента на его динамические характеристики представим альтернативные выражения для амплитуды колебаний:
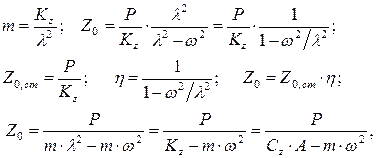 (8.5)
(8.5)
где Z0, ст – осадка фундамента от статического действия динамической нагрузки; h – коэффициент динамичности.
Необходимо обратить внимание на то, что в формулах (8.4, 8.5) частота собственных колебаний фундамента l имеет размерность 1/с, а частота вынужденных колебаний w рад/с. Таким образом, паспортную частоту вынужденных колебаний динамической нагрузки f, выраженную в гц, нужно приводить к круговой частоте умножением на 2×p. Студентам предлагается убедиться в справедливости формул (8.3 – 8.5), несмотря на кажущуюся некорректность размерностей входящих в них частот собственных и вынужденных колебаний, повторив выводы этих формул для динамической нагрузки P×sin(2×p×f × t) и приняв в конечных выражениях 4×p2×f2 = w2.
 Анализируя формулы (8.5), можно сделать следующие выводы. Коэффициент динамичности зависит от соотношения частот собственных и вынужденных колебаний фундамента. Его значение принимается по абсолютной величине и стремится к единице при отходе от резонанса в область низкочастотных колебаний. При отходе от резонанса в область высоких частот этот коэффициент стремится к нулю. Амплитуда колебаний уменьшается при увеличении жесткости основания и площади опирания фундамента, а также при уменьшении массы фундамента. Фундаменты одной и той же массы имеют меньшую амплитуду колебаний, если они в большей степени развиты в плане (рис. 8.2).
Анализируя формулы (8.5), можно сделать следующие выводы. Коэффициент динамичности зависит от соотношения частот собственных и вынужденных колебаний фундамента. Его значение принимается по абсолютной величине и стремится к единице при отходе от резонанса в область низкочастотных колебаний. При отходе от резонанса в область высоких частот этот коэффициент стремится к нулю. Амплитуда колебаний уменьшается при увеличении жесткости основания и площади опирания фундамента, а также при уменьшении массы фундамента. Фундаменты одной и той же массы имеют меньшую амплитуду колебаний, если они в большей степени развиты в плане (рис. 8.2).
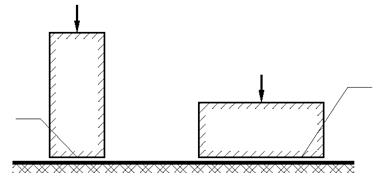
| Рис. 8.2. Зависимость амплитуды колебаний фундаментов одной массы от площади опирания на основание: m – масса фундамента; А1, А2 – площадь подошвы фундамента; Z0,1, Z0,2 – амплитуда колебаний; P×sin w t – динамическая нагрузка. |
 При действии по верху фундамента горизонтальной периодической нагрузки Px×sin w t (рис. 8.3) возникают горизонтальные и угловые колебания фундамента, амплитуды которых определяются по формулам:
При действии по верху фундамента горизонтальной периодической нагрузки Px×sin w t (рис. 8.3) возникают горизонтальные и угловые колебания фундамента, амплитуды которых определяются по формулам:
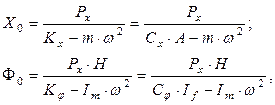 (8.6)
(8.6)
где Н – плечо приложения силы Px относительно подошвы фундамента;
Im – момент инерции массы всей установки относительно оси, проходящей через общий центр тяжести перпендикулярно плоскости колебаний (кг×м2 или кН×м×с2).
Фундаменты под электрические машины и турбоагрегаты при скорости вращения n > 1000 об/мин (f = 16,67 гц, w = 105 рад/с) на динамические нагрузки не рассчитываются, за исключением нагрузок пускового периода.
 Расчет фундаментов на динамические нагрузки ударного действия. Динамические нагрузки ударного действия возникают при работе штамповочных и ковочных молотов. Молот состоит (рис. 8.4) из станины, подвижной части (молота), шабота, подшаботных прокладок, подшаботной плиты и фундамента.
Расчет фундаментов на динамические нагрузки ударного действия. Динамические нагрузки ударного действия возникают при работе штамповочных и ковочных молотов. Молот состоит (рис. 8.4) из станины, подвижной части (молота), шабота, подшаботных прокладок, подшаботной плиты и фундамента.
Масса фундамента (т) и площадь подошвы фундамента определяются по эмпирическим формулам:
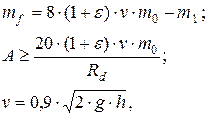 (8.7)
(8.7)
где m0 и m1 – соответственно масса молота и масса станины с шаботом (т);
v – скорость молота в момент, предшествующий удару (м/с); h – высота падения молота; g – ускорение свободного падения; e - коэффициент восстановления удара, зависящий от упругих свойств соударяющихся частей; Rd – расчетное сопротивление грунта; mf и A – соответственно масса фундамента с грунтом на его свесах и площадь подошвы фундамента.
Коэффициент восстановления удара e принимается: при штамповке стальных изделий – 0,5; при штамповке изделий из цветных металлов – 0; при ковке – 0,25. Скорость молота и его масса зависят от конструкции машины. Различают легкие, средние и тяжелые молоты. Для легких молотов (масса до 1 т) скорость в момент удара составляет 8 м/с. Масса средних молотов изменяется от 1 до 3 т , а скорость составляет 7 м/с. Тяжелые молоты массой более 3 т имеют скорость 6,5 м/с. После назначения конструктивных параметров фундамента с учетом рекомендуемых параметров по формулам (8.7) определяют амплитуду вертикальных колебаний фундамента:
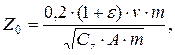 (8.8)
(8.8)
где m – масса станины, молота, шабота и фундамента с грунтом на свесах;
С z – коэффициент упругости основания по формулам (8.1).
Полученное значение амплитуды вертикальных колебаний фундамента сравнивается с допускаемой нормами величиной. Если установленные нормами ограничения амплитуды вертикальных колебаний не выполняются, производят переопределение конструктивных параметров фундамента, например, увеличивают площадь его подошвы, увеличивают жесткость основания и т.п.
Распространение колебаний в грунтовом массиве. Динамические нагрузки на фундаменты возбуждают колебания в окружающем его грунтовом массиве (рис. 8.5). При этом оказываются динамические воздействия на расположенные в непосредственной близости здания и сооружения. Процесс распространения упругих волн в грунтовом массиве является затухающим и оценивается коэффициентом относительной диссипации.

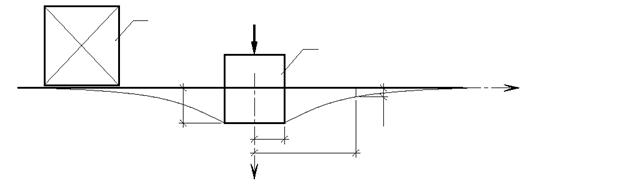
Рис. 8.5. Схема распространения колебаний в грунтовом массиве: 1 – источник колебаний; 2 – объект, на который оказывается влияние динамического воздействия; Z0, Zr – амплитуды колебаний; r0, r – радиусы зон распространения колебаний.
Практически колебания в грунтовом массиве могут оказывать влияние на объекты строительства, расположенные на расстоянии десятков и сотен метров от источника колебаний, например, от железнодорожной магистрали. Затухание амплитуды поверхностной волны в массиве может быть оценено по формуле:
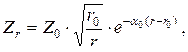 (8.9)
(8.9)
где Zr, Z0 – амплитуда колебаний на расстоянии r и r0 от источника колебаний (центра фундамента); r0 - радиус источника колебаний (фундамента); a0 – коэффициент поглощения энергии волн (м-1).
Величина коэффициента поглощения энергии волн зависит от вида грунтов, слагающих массив, и принимается равной: для слабых пылевато-глинистых грунтов 0,03–0,04; для песков 0,04–0,06; для плотных глин 0,06–0,1.
Виброгасители колебаний. Предназначены для изменения частотных характеристик системы “основание – фундамент – верхнее строение” с целью уменьшения амплитуд вынужденных колебаний фундамента. Как уже было показано выше, динамический коэффициент колебательного процесса уменьшается при удалении частоты собственных колебаний конструктивной системы от частоты вынужденных колебаний (динамической нагрузки). На практике это достигается применением виброгасителей колебаний. Различают два основных типа виброгасителей: виброгасители с присоединенными массами (рис. 8.6 б); виброгасители с пружинами – амортизаторами (рис. 8.6 а). Шарнирно присоединенные массы значительно увеличивают площадь подошвы фундамента и незначительно увеличивают его массу. В соответствии с формулами (8.5) это приводит к уменьшению амплитуды колебаний фундамента. Жесткостные характеристики пружин – амортизаторов подбираются таким образом, чтобы исключить явление резонанса при работе динамической машины.

Дата: 2019-03-05, просмотров: 842.