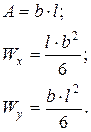Основание столбчатых фундаментов всегда рассчитывается по деформациям и в отдельных случаях (см. лекцию 1) по несущей способности. Конструкции столбчатого фундамента рассчитываются по прочности и ширине раскрытия трещин (для железобетонных фундаментов).
1. Определение размеров подошвы фундамента в плане. Расчет выполняется на действие расчетных нагрузок для II группы предельных состояний из условия ограничения давлений на основание до такого уровня, при котором расчет осадок основания может производится по линейной теории. Эпюры контактных давлений в этих расчетах принимаются линейными (см. лекцию 4 курса "Механика грунтов"). В качестве исходных данных задаются такие параметры (рис. 4.1): d – глубина заложения фундамента; hf – высота фундамента; g a – осредненный удельный вес фундамента и грунта на его свесах, принимаемый при отсутствии точных данных 20 кН/м3; q – пригруз на поверхности основания от складируемых материалов и транспортных средств, принимаемый не менее 20 кН/м2 для промышленных зданий и 10 кН/м2 для гражданских зданий; N – продольная сила на обрезе фундамента; Qy, Qx – поперечные силы на уровне обреза фундамента по направлению поперечной (y) и продольной (x) оси фундамента; Mx, My – изгибающие моменты в сечении обреза фундамента относительно продольной (x) и поперечной (y) оси фундамента; A – площадь подошвы фундамента; Wx, Wy – моменты сопротивления площади подошвы фундамента относительно продольной (x) и поперечной (y) оси площади подошвы; R – расчетное сопротивление грунта. Ниже приводятся четыре условия, ограничивающие среднее давление по подошве фундамента, давление в угловой точке и давления на серединах сторон фундамента:
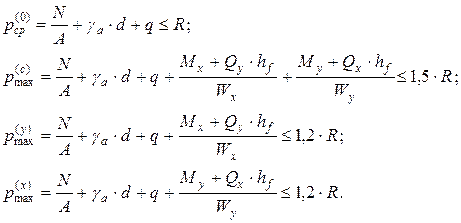 (4.1)
(4.1)
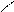
| Рис. 4.1. Расчётная схема к проверке давлений под подошвой фундамента столбчатого фундамента: N, Qx, Qy, Mx, My – усилия, приложенные к обрезу фундамента; q – пригруз; gа – усреднённый удельный вес грунта обратной засыпки и фундамента; Рср, Р min, Pmax – среднее, минимальное и максимальное давления под подошвой фундаментов; А, Wx, Wy – площадь подошвы и моменты сопротивления площади подошвы фундаментов; (0), (y), (х), (с) – контрольные точки при проверке давлений на основание.
| |
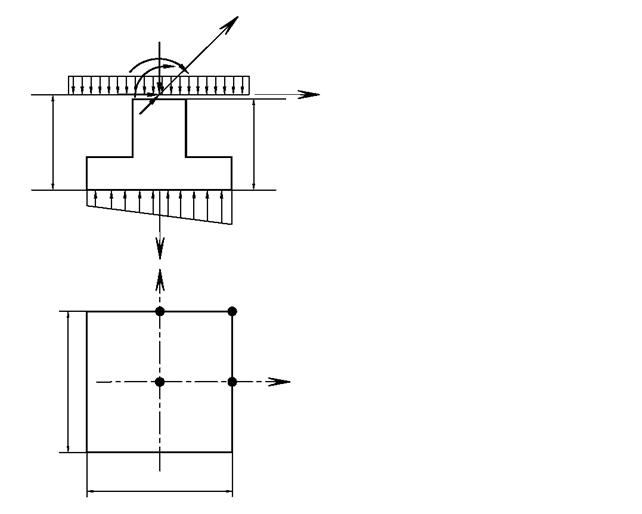
Из решения системы неравенств (4.1) определяют ширину подошвы фундамента b и длину l. Обычно задаются отношением k = l / b, в связи, с чем определению подлежит только ширина подошвы фундамента b, так как ее длина l = k×b. Систему неравенств (4.1) часто решают графическим методом (рис. 4.2).
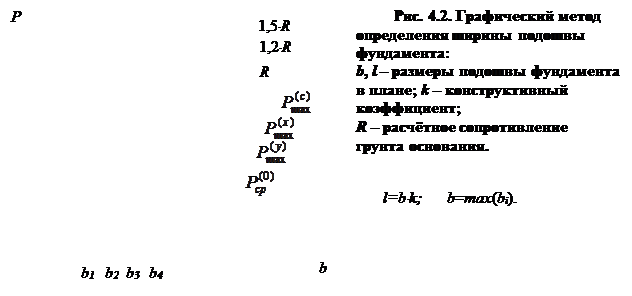
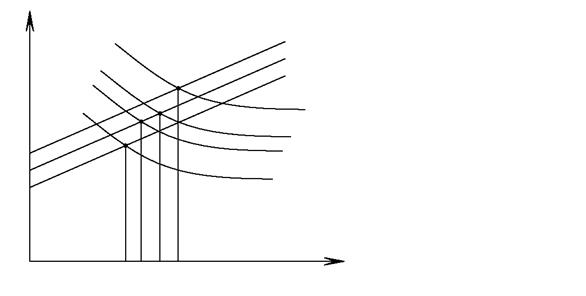
Для этого в координатной плоскости с осями b, p строят графики левых и правых частей неравенств (4.1). Абсциссы точек пересечения этих графиков являются граничными значениями ширины подошвы фундамента bi в неравенствах (4.1). В качестве расчетного значения ширины подошвы фундамента принимают максимальное значение из найденных граничных значений: b = max (bi).
2. Расчет осадок фундамента. Расчет осадок фундамента выполняется методом послойного суммирования или методом линейно-деформируемого слоя (см. лекцию 8 курса "Механика грунтов") по расчетным нагрузкам и характеристикам грунтов для II группы предельных состояний. При этом в необходимых случаях учитывают влияние соседних фундаментов. В том случае, если абсолютные и относительные осадки фундамента не удовлетворяют требованиям норм (см. лекцию 1), производят корректировку конструктивных параметров фундамента с целью уменьшения осадок основания. Уменьшение осадок основания достигается увеличением размеров подошвы фундамента и увеличением глубины заложения фундамента. Если указанными мерами не достигается необходимое уменьшение осадок основания, прибегают к мерам, связанным с улучшением свойств грунтов, слагающих основание, или переходят на фундаменты другой конструктивной системы, например, на свайные фундаменты.
3. Расчет фундаментной плиты на продавливание. Фундаментные плиты, как правило, не имеют поперечного (вертикального) армирования, в связи с чем поперечные силы воспринимаются исключительно материалом фундамента (бетоном). Экспериментальными исследованиями установлено, что разрушение фундаментной плиты от действия поперечных сил происходит по схеме отрыва со скалыванием по граням пирамиды продавливания (рис. 4.3).

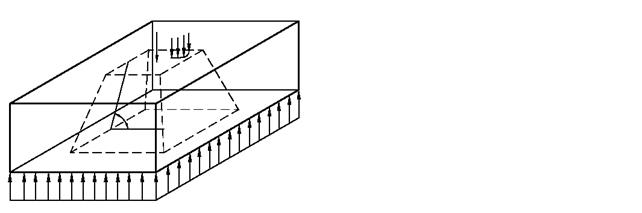
Меньшим основанием пирамиды продавливания является опорное сечение колонны или подколонника. Большим основанием пирамиды продавливания является площадь подошвы фундамента, ограниченная линиями пересечения подошвы фундамента с боковыми гранями пирамиды продавливания. Боковые грани пирамиды продавливания наклонены к горизонтальной плоскости под углом 45°. Нормальные напряжения на меньшем основании пирамиды продавливания, вызванные нагрузкой от колонны, уравновешиваются давлением грунта на большее основание и проекциями на вертикальную ось нормальных растягивающих напряжений, действующих на наклонных гранях пирамиды продавливания. Высота пирамиды продавливания h0 измеряется от опорного сечения колонны или подколонника (при высоком подколоннике) до центра тяжести нижней рабочей арматуры в фундаментной плите (рис. 4.4).

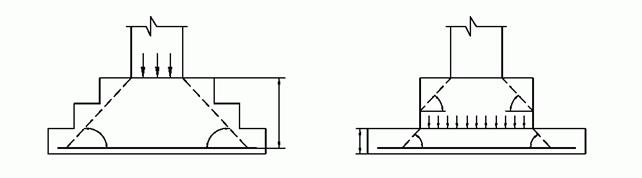
Рис. 4.4. Схема к определению высоты пирамиды продавливания: а – при низком подколоннике, б – при высоком подколоннике.
В сборно-монолитных фундаментах допускается опорное сечение колонны принимать на уровне обреза фундамента. Пирамида продавливания не должна выходить за границы фундамента. Последнее может иметь место при высоком подколоннике (рис. 4.4, б). Если указанное выше имеет место, высота пирамиды продавливания измеряется от опорного сечения подколонника.
Различают два вида расчетов на продавливание: продавливание по четырем сторонам; продавливание по короткой стороне. Расчет на продавливание по четырем сторонам выполняют для центрально нагруженных прямоугольных в плане фундаментов. Во всех остальных случаях выполняют расчет на продавливание по короткой стороне. Расчеты выполняются по расчетным нагрузкам на фундаменты для I группы предельных состояний.
Расчет на продавливание по четырем сторонам. Обозначим размеры меньшего основания пирамиды продавливания buc и luc (рис. 4.5).
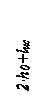
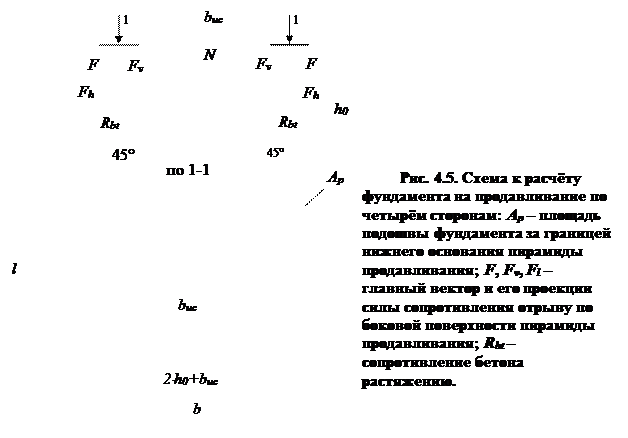
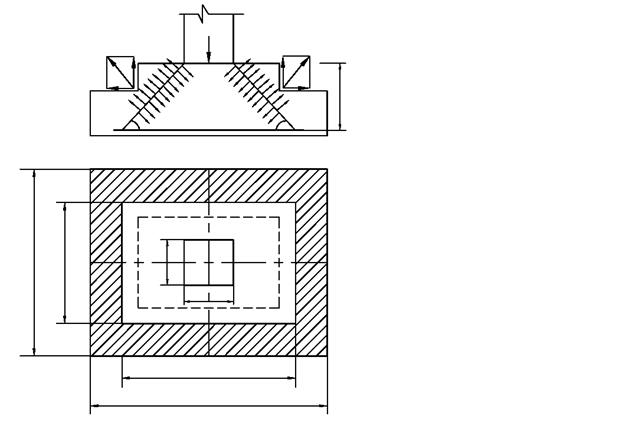
Вычислим средний периметр боковой поверхности пирамиды продавливания bp и площадь ее большего основания Ap:
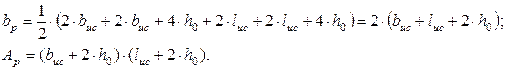 (4.2)
(4.2)
Продавливающую силу Q определим как давление грунта на подошву фундамента за границами пирамиды продавливания. Сумма проекций на вертикальную ось нормальных растягивающих напряжений в бетоне Rbt, действующих в предельном состоянии на боковой поверхности S пирамиды продавливания, Fv представится произведением этих напряжений на вертикальную проекцию площади боковых граней пирамиды продавливания S×cos 45° = bp×h0. Условие продавливания фундаментной плиты по четырем сторонам имеет вид:
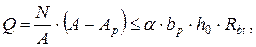 (4.3)
(4.3)
где a – коэффициент, принимаемый 1,0 для тяжелого, 0,85 для мелкозернистого и 0,8 для легкого бетона.
Расчет на продавливание по короткой стороне. Предполагается, что продавливание происходит по схеме отрыва со скалыванием по боковой грани пирамиды продавливания, примыкающей к короткой стороне подошвы фундамента со стороны максимального давления на грунт (рис. 4.6).
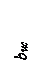
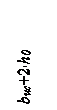
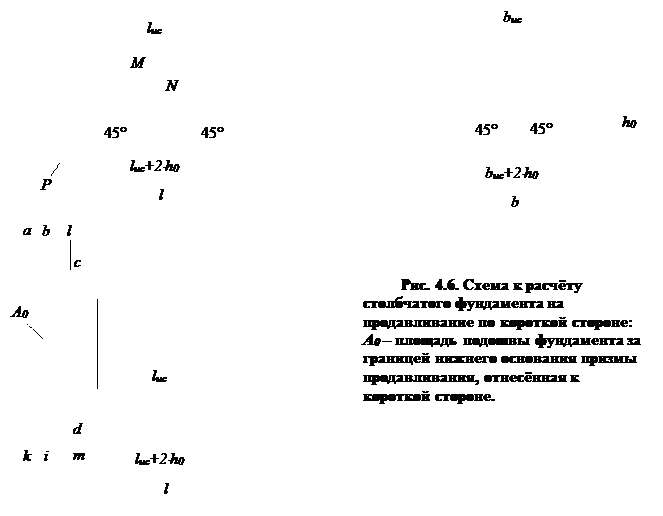
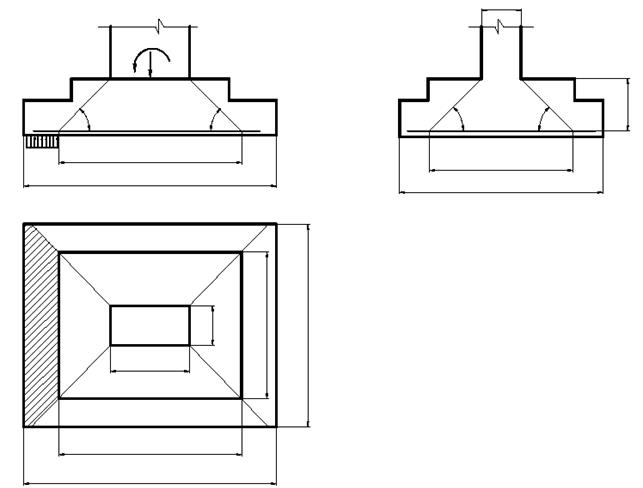
Продавливающую силу Q определяют как произведение максимального давления грунта на площадь подошвы фундамента A0 за пределами пирамиды продавливания, отнесенную к рассматриваемой боковой грани пирамиды продавливания. Для нахождения указанной площади на плане фундамента продолжают проекции ребер пирамиды продавливания до их пересечения со сторонами подошвы фундамента (линии cb и di на рис. 4.6). Кроме этого продлевают сторону cd большего основания пирамиды продавливания до ее пересечения со сторонами подошвы фундамента (линии cl и dm на рис. 4.6). Искомую площадь подошвы фундамента определяют как разность площади прямоугольника almk и двух треугольников – cbl и dim. Расчетные формулы имеют вид:
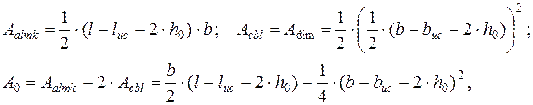 (4.4)
(4.4)
где l, b – длина и ширина подошвы фундамента; luc, buc – длина и ширина сечения колонны (подколонника); h0 – высота пирамиды продавливания.
Максимальные давления грунта на площадь подошвы фундамента А0 определяют как максимальное напряжение по середине короткой стороны (4.1), т.е. с учетом действия изгибающего момента относительно поперечной оси фундамента (но без учета g a и q):
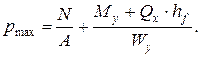 (4.5)
(4.5)
Площадь проекции боковой грани пирамиды продавливания на вертикальную плоскость, проходящую через поперечную ось фундамента, будет равна произведению полусуммы оснований боковой грани на высоту пирамиды продавливания. Полусумма оснований боковой грани пирамиды продавливания определяется выражением:
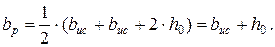 (4.6)
(4.6)
С учетом сделанных определений проверка продавливания фундаментной плиты по короткой стороне выполняется в соответствии с выражением:
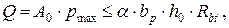 (4.7)
(4.7)
где a - то же, что в формуле (4.3).
Если фундаментная плита имеет переменное ступенчатое сечение, выполняются проверки на ее продавливание под каждой ступенью, которая рассматривается как подколонник. При этом длина консольного выноса плиты под ступенью должна быть не менее толщины плиты (условие сплошности тела пирамиды продавливания). Если условия (4.3) или (4.7) не выполняются, увеличивают толщину плиты или назначают более высокий класс бетона по прочности.
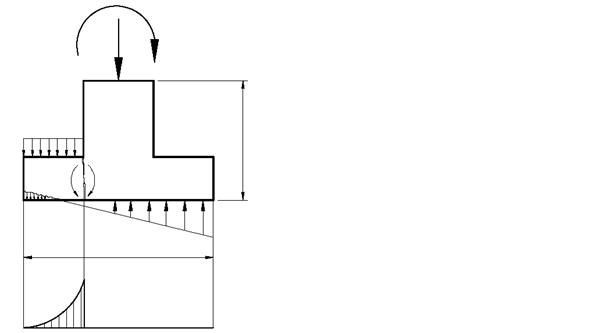
4. Расчет фундаментной плиты на изгиб. Расчету подлежат нормальные сечения плиты в месте изменения ее толщины. Такими сечениями являются сечения по грани подколонника или по грани ступени (рис. 4.7). Плита рассчитывается как консольная балка длиной с, защемленная в расчетном сечении и загруженная давлением грунта. Эпюра давлений грунта от действия расчетных нагрузок для I группы предельных состояний принимается трапециевидной с максимальным давлением pmax по краю консоли.

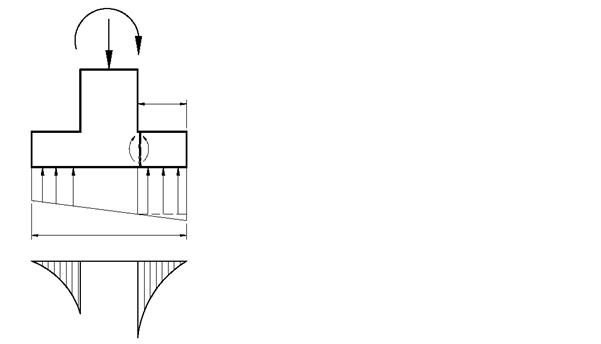
Давление в расчетном сечении рс определяется по максимальному pmax и минимальному pmin давлениям по краям фундамента. Расчет ведется на единицу ширины плиты. По результатам расчета назначается площадь сечения рабочей арматуры плиты As в продольном и поперечном направлении. Плита армируется сетками в нижней зоне. С целью оптимизации армирования плиты рабочая арматура может иметь обрывы при приближении к краям фундаментной плиты. Изгибающий момент в расчетном сечении плиты (на единицу ее длины) определяется по формуле:
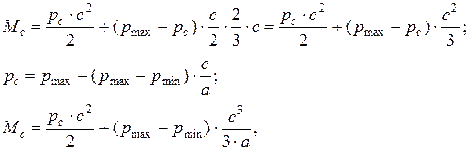 (4.8)
(4.8)
где a – длина l или ширина b фундамента.
При pmin < 0 выполняется проверка нормального сечения плиты на действие обратного изгибающего момента от нагрузки консоли весом грунта, лежащего выше подошвы фундамента (рис. 4.8).
Проверка выполняется на единицу длины плиты по формулам:
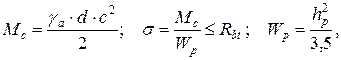 (4.9)
(4.9)
где hp - толщина фундаментной плиты в расчетном сечении;
Wp - пластический момент сопротивления расчетного сечения плиты единичной ширины.

5. Расчет подколонника. Подколонник имеет рабочую продольную арматуру (рис. 4.9), заанкеренную в уровне подошвы фундамента.
Расчет нормальных сечений подколонника выполняется по аналогии с расчетом нормальных сечений колонны на внецентренное сжатие. При подколоннике стаканного типа проверяется коробчатое сечение в уровне пяты колонны. Изгибающие моменты в расчетном сечении подколонника определяются по формулам:
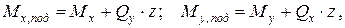 (4.10)
(4.10)
где z – расстояние от обреза фундамента до расчетного сечения подколонника.

Продольная сила в расчетном сечении подколонника принимается равной ее значению на обрезе фундамента. При подколоннике стаканного типа производится проверка на смятие бетона под колонной. При этом должно выполняться условие:
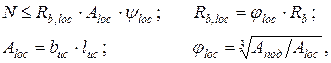 (4.11)
(4.11)
где y loc – коэффициент, принимаемый равным 1,0 при малых эксцентриситетах приложения нагрузки (e0 £ a / 6) и 0,75 при больших эксцентриситетах (e0 > a / 6); Апод – площадь поперечного сечения подколонника; Rb – расчетное сопротивление бетона сжатию.
6. Расчет стакана. Расчетом определяется поперечное армирование стакана и выполняется проверка на его раскалывание при возможном проскальзывании заделанной в нем колонны. Расчетное наклонное сечение стакана (рис. 4.10) при действии изгибающего момента и поперечной силы (нагрузки для I группы предельных состояний) назначается в зависимости от эксцентриситета приложения нагрузки e0 = (My + Qx×zс) / N. При e0 < luc / 6 поперечное армирование стакана назначается конструктивно. При e0 > luc / 2 расчетное сечение проходит через крайнюю точку на обрезе фундамента и угловую точку внутри стакана OI.

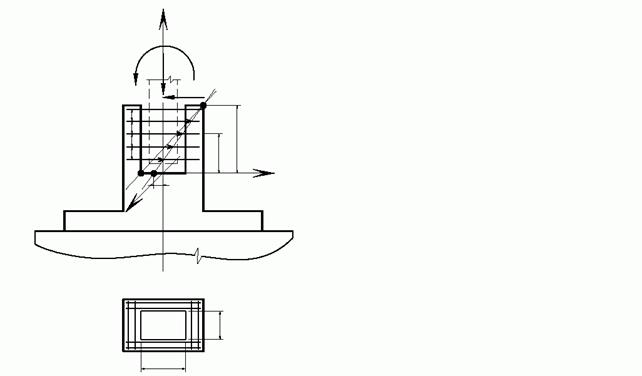
Выполняется проверка указанного наклонного сечения на действие изгибающего момента. Из условия равновесия моментов всех сил, действующих в наклонном сечении, определяется площадь сечения поперечной арматуры Asw, которая относится к двум параллельным стенкам стакана:
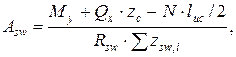 (4.12)
(4.12)
где zc – глубина стакана; Rsw – расчетное сопротивление поперечной арматуры; zsw, i – расстояние от i–го стержня поперечной арматуры до дна стакана.
При luc / 2 ³ e0 ³ luc / 6 расчетное наклонное сечение проходит через точку OII, отстоящую от центра стакана на luc / 6. Подбор поперечной арматуры в этом случае производится по формуле:
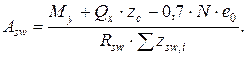 (4.13)
(4.13)
Рассматриваются две возможные схемы раскалывания фундамента по продольной и поперечной оси (рис. 4.11).




| Рис. 4.11. Схема к расчёту фундамента с подколонником стаканного типа на раскалывание: Al – расчётная площадь плиты при раскалывании вдоль длинной стороны; Ab – то же вдоль короткой стороны.
| |
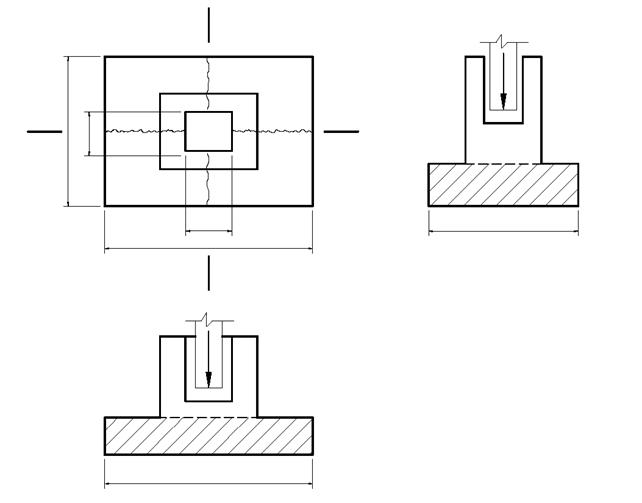
Предполагается, что раскалыванию фундамента препятствует фундаментная плита, работающая на растяжение в продольном Al или в поперечном Ab сечении. Проверка на раскалывание фундамента сводится к выполнению двух условий:
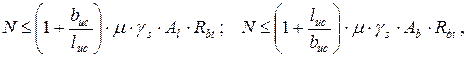 (4.14)
(4.14)
где m - коэффициент трения, принимаемый равным 0,75; g s – коэффициент, равный 1,3.
7. Расчет фундаментной плиты по ширине раскрытия трещин. Расчет выполняется по нормам на проектирование железобетонных конструкций. Проверяется ширина раскрытия трещин в нормальных сечениях плиты на гранях ступеней и подколонника при действии изгибающих моментов, вычисленных от действия расчетных нагрузок для второй группы предельных состояний (см. лекцию 1). При недопустимых значениях ширины раскрытия трещин увеличивают армирование фундаментной плиты.
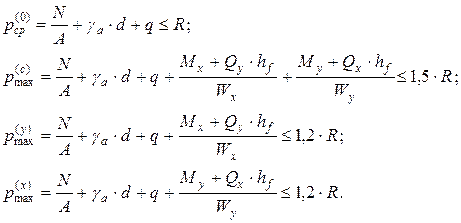 (4.1)
(4.1)
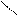






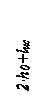
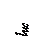


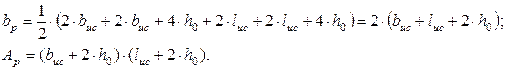 (4.2)
(4.2)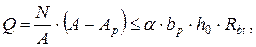 (4.3)
(4.3)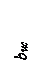
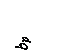
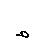
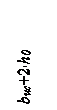


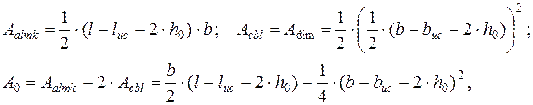 (4.4)
(4.4)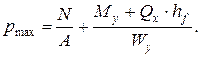 (4.5)
(4.5)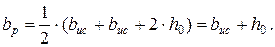 (4.6)
(4.6)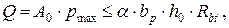 (4.7)
(4.7)

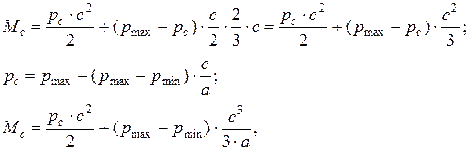 (4.8)
(4.8)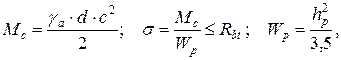 (4.9)
(4.9)

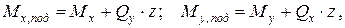 (4.10)
(4.10)
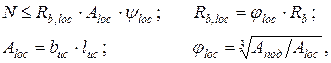 (4.11)
(4.11)

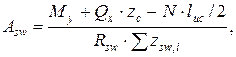 (4.12)
(4.12)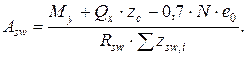 (4.13)
(4.13)




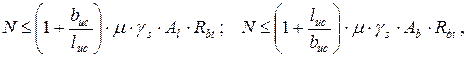 (4.14)
(4.14)