 1. Конструкции ленточных фундаментов. Ленточные фундаменты предназначены для передачи нагрузок на основание от стен. Они также могут использоваться для передачи больших нагрузок от колонн, когда определенные по расчету площади подошвы столбчатых фундаментов сливаются в одну ленту. Ленточный фундамент (рис. 5.1) состоит из фундаментной плиты и из фундаментной балки.
1. Конструкции ленточных фундаментов. Ленточные фундаменты предназначены для передачи нагрузок на основание от стен. Они также могут использоваться для передачи больших нагрузок от колонн, когда определенные по расчету площади подошвы столбчатых фундаментов сливаются в одну ленту. Ленточный фундамент (рис. 5.1) состоит из фундаментной плиты и из фундаментной балки.
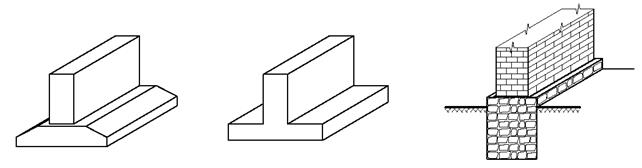
Рис. 5.1. Конструктивные элементы ленточного фундамента: а – сборного железобетонного; б – монолитного железобетонного; в – каменного.
Фундаментная балка часто выполняет функции стены подвала или другой ограждающей конструкции подземной части сооружения. В монолитных фундаментах фундаментная плита и балка представляют собой единую балочную конструкцию таврового поперечного сечения. В каменных фундаментах малоэтажных зданий нагрузка на основание может непосредственно передаваться фундаментной балкой, представляющей собой заглубленную в основание каменную стену. Ленточные фундаменты устраиваются по осям продольных и поперечных несущих стен здания, образуя пространственную фундаментную конструкцию. Пролетом ленточного фундамента называют расстояние между пересекающими его поперечными или продольными стенами. При величине отношения высоты балки ленточного фундамента к ее пролету более 0,5 фундаментную балку называют балкой – стенкой. Балки – стенки рассматриваются в расчетах фундамента как пластинчатые конструкции, в то время как балки представляются стержневыми конструкциями. Поскольку ленточный фундамент является пространственной конструкцией, его работа анализируется в продольном и в поперечном направлениях. Тип фундамента по жесткости в продольном направлении устанавливается как для балки на упругом основании (см. лекцию 2). При этом монолитный фундамент рассматривается как балка таврового поперечного сечения, а жесткость сборного фундамента определяется без учета сечения фундаментной плиты. В поперечном направлении тип фундамента по жесткости устанавливается как для столбчатого фундамента (см. лекцию 3). В строительстве широко используются сборные ленточные фундаменты из типовых конструкций (рис. 5.1 а). Фундаментные плиты по типовой серии 1.112-5 имеют переменное поперечное сечение с максимальной высотой в месте опирания стены 300 и 500 мм. Длина фундаментных плит 0,8, 1,2 и 2,4 м, ширина 0,8, 1,0, 1,2, 1,4, 1,6, 2,0, 2,4, 2,8 и 3,2 м. Плиты изготавливаются из бетона класса по прочности В10–В25 и армируются сетками в уровне подошвы. Существует вариант облегченных плит ребристой конструкции. Маркировка плиты включает буквы «ФЛ» и две цифры, разделенные запятой, обозначающие ширину и длину плиты в дециметрах. Например, маркировка ФЛ 16,24 обозначает фундамент ленточный с шириной подошвы 1,6 м и длиной 2,4 м. Стены сборных ленточных фундаментов изготавливают из стеновых фундаментных блоков по ГОСТ 13579 – 78. Маркировка блоков состоит из букв «ФБС» и цифры, обозначающей толщину блока в дециметрах. Блоки изготавливаются высотой 600 мм и длиной 800 и 2400 мм. Толщина блоков принимается 300, 400, 500 и 600 мм. Наряду с основными блоками имеются также доборные блоки высотой 300 мм. Стеновые фундаментные блоки монтируются в конструкцию фундамента на растворе с перевязкой вертикальных швов в каждом ряду. Между блоками могут устраиваться монолитные бетонные вставки для равномерного заполнения стены фундамента, если ее длина не является кратной 800 мм. Блоки укладываются с перевязкой по углам фундамента и в местах пересечений стен. Горизонтальные швы между блоками в местах пересечения стен армируются, как правило, горизонтальными сетками при отсутствии перевязки. Имеется разновидность стеновых фундаментных блоков с прямоугольными вертикальными пустотами (рис. 5.2 а). Такие конструкции используются для устройства сборно-монолитных ленточных фундаментов. Фундаментные плиты в этом случае устраиваются монолитными с вертикальными выпусками арматуры. Указанные выпуски арматуры заводятся в пустоты стеновых блоков и стыкуются с арматурными каркасами, устанавливаемыми в этих пустотах. По верху такая конструкция объединяется монолитной железобетонной балкой, называемой цокольным поясом. Как правило, в цокольном поясе устраивается четверть для опирания плит перекрытия первого этажа. 
В крупнопанельных зданиях стены ленточного фундамента устраиваются из цокольных панелей (рис. 5.2 б). Цокольные панели монтируются на растворе по фундаментным плитам. Между собой цокольные панели сопрягаются с помощью сварных или петлевых стыков. Стыки устраиваются по осям пресекающихся продольных и поперечных стен. Стыки выпусков арматуры на сварке и петлевые стыки совмещаются с устройством в месте сопряжения цокольных панелей бетонных шпонок.

Как правило, в пределах отсека здания или сооружения ленточные фундаменты устраиваются на одной отметке. При необходимости изменения глубины заложения фундамента в пределах отсека (рис. 5.3) отметки фундаментных плит изменяют ступенями от более заглубленной к менее заглубленной части фундамента с подбетонкой под плитами со стороны более заглубленной части фундамента.


Сборные фундаментные плиты ленточного фундамента могут монтироваться на основание с расчетными разрывами по длине, а также могут иметь вырезы в плане по углам (рис. 5.4). Такие фундаменты называются прерывистыми. При одинаковой со сплошными фундаментами несущей способности прерывистые фундаменты являются более экономичными.
Разновидностью ленточных фундаментов являются щелевые фундаменты (рис. 5.5), устраиваемые бетонированием враспор траншей или щелей в грунте.

В основании может устраиваться одна, две, три и более щелей, заполняемых бетоном. Полученная таким образом конструкция объединяется фундаментной балкой, называемой ростверком, на которую опирается стена ленточного фундамента. Характерной особенностью такого фундамента является отсутствие фундаментной плиты, роль которой выполняет размещенный между стенами в грунте объем грунта, имеющий повышенную прочность за счет эффекта обоймы (сдерживания поперечных деформаций грунта ограничивающими его стенами). По схеме взаимодействия с основанием такой фундамент, скорее всего, относится к фундаментам глубокого заложения, так как нагрузки на основание воспринимаются не только вертикальными напряжениями по подошве, но и силами трения и сцепления по боковым поверхностям стен в грунте.
2. Конструкции плитных фундаментов. Плитные фундаменты передают нагрузки на основание от сильно нагруженных стен и колонн. Применяются в тех случаях, когда определенные расчетом площади подошвы ленточных и столбчатых фундаментов сливаются в одну плиту. Различают сплошные плиты, плиты переменного сечения, как правило, подкрепленные ребрами и коробчатые плиты (рис. 5.6).

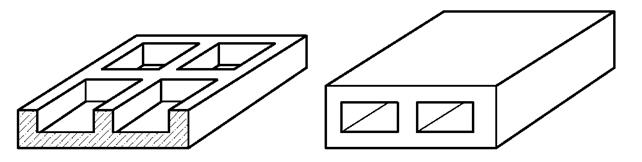
Рис. 5.6. Конструкции плитных фундаментов переменного сечения: а – ребристые; б – коробчатые.
Толщину плит принимают от 300 до 1200 мм. Для таких сооружений как силосы, угольные башни толщина фундаментной плиты может составлять 1500 – 2000 мм. Фундаментные плиты устраивают на уплотненном основании по бетонной подготовке толщиной 100 мм. Как правило, плиты армируют горизонтальными сетками в нижней и верхней зонах. Поперечное вертикальное армирование применяется в исключительных случаях, когда при заданной толщине плиты не удается воспринять расчетные поперечные силы сопротивлением бетона растяжению по наклонным сечениями. Плиты переменного сечения можно представить как столбчатые или ленточные фундаменты, объединенные между собой общей плитой в уровне нижней ступени. Если такое объединение выполняется для ленточных фундаментов, фундаментные балки ленточных фундаментов выполняют функцию ребер, подкрепляющих плиту. В том случае, если объединяются общей плитой ленточные фундаменты в виде системы перекрестных балок – стенок, образуется конструкция коробчатой плиты. Повышение жесткости такого фундамента может быть достигнуто включением в совместную работу конструкций ниже нуля монолитного или сборно-монолитного перекрытия над подвалом. Примером фундаментной плиты коробчатой конструкции может являться сплошная плита (рис. 5.7), сопряженная со сборно-монолитными стенами, устроенными из пустотных стеновых фундаментных блоков (см. п. 1). Фундаментная плита является сложной пространственной конструкцией на упругом основании в связи с чем, ее конструктивные параметры определяются на основании расчетов с использованием ЭВМ.

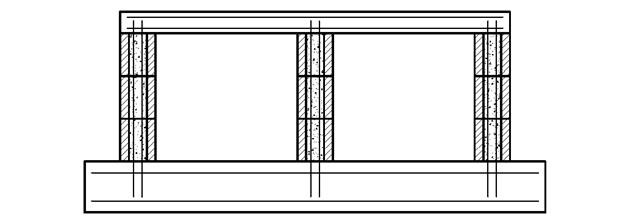
Рис. 5.7. Сборно-монолитный коробчатый плитный фундамент:
1 – фундаментная плита; 2 – плита перекрытия; 3 – пустотелые фундаментные блоки; 4, 5, 6 – рабочая арматура в плитах и блоках; 7 – бетон омоноличивания.
3. Расчет ленточных фундаментов. Как уже отмечалось, ленточный фундамент является сложной пространственной конструкцией. С целью упрощения расчета рассматривается работа фундамента в поперечном и в продольном направлениях. При этом решаются плоские задачи, а результаты таких решений суммируются.
3.1. Определение ширины подошвы ленточного фундамента. Поскольку ленточный фундамент является протяженной конструкцией, расчеты выполняются для фрагмента длиной 1 м. Ширина подошвы ленточного фундамента здания без подвала определяется так же, как для столбчатого фундамента (см. лекцию 4). При этом используются только два условия ограничения давлений на основание: рср £ R; pmax £ 1,2×R.
Для здания с подвалом ширина подошвы ленточного фундамента определяется следующим образом. Составляется схема нагрузок, действующих на фундамент (рис. 5.8), и вычисляются равнодействующие сил на уровне подошвы фундамента: продольная сила N, изгибающий момент M и поперечная сила Q. Силы N и M определяются с учетом собственного веса фундамента и веса грунта на консолях фундаментной плиты, а также с учетом пригруза на поверхности основания. При жестком сопряжении стены подвала с фундаментной плитой изгибающий момент М определяется с учетом действия на стену подвала активного давления грунта Еа (см. лекцию 4 курса "Механика грунтов"). Поперечная сила Q определяется с учетом активного давления грунта на стену подвала и пассивного давления грунта со стороны пола подвала.

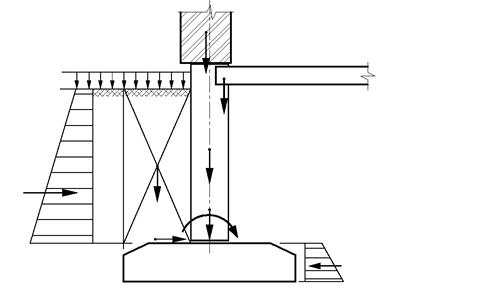
В связи с тем, что расчетные усилия определяются с учетом временных нагрузок (пригруза на поверхности основания), составляется несколько основных расчетных сочетаний, в которых варьируется присутствие временной нагрузки. Например, при наличии пригруза только с наружной стороны стены подвала составляется два основных сочетания – с учетом и без учета пригруза. Ширина подошвы ленточного фундамента определяется из решения графическим методом двух неравенств:
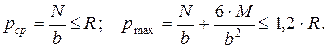 (5.1)
(5.1)
В уравнениях (5.1) силы N и M относятся к единице длины ленточного фундамента и имеют размерности соответственно кН/м и кН×м/м. Расчеты по формулам (5.1) выполняются для всех основных сочетаний нагрузок, а в качестве расчетной величины принимается максимальное значение ширины подошвы фундамента из этих расчетов.
3.2. Определение осадки ленточного фундамента. Осадка ленточного фундамента рассчитывается методом послойного суммирования для расчетных поперечных сечений, отличающихся глубиной заложения фундамента, расчетными нагрузками и геологическими разрезами. По результатам этих расчетов проверяется выполнение нормативных ограничений по значениям абсолютных и относительных осадок фундамента. Если указанные ограничения не выполняются, производят увеличение ширины фундамента на отдельных участках или по всей длине. После этого осадки фундамента рассчитываются заново. Если ленточный фундамент имеет жесткую в продольном направлении балку или балку – стенку, способную выравнивать осадки по длине фундамента, расчеты по определению осадок в расчетных сечениях ленточного фундамента используются для определения коэффициентов жесткости основания. Эта информация используется для расчета ленточного фундамента как балки на упругом основании.
3.3. Проверка прочности основания ленточного фундамента. Поскольку основание ленточного фундамента здания с подвалом испытывает горизонтальные нагрузки, требуется проверка его прочности (устойчивости). Прочность основания проверяется по двум схемам потери устойчивости: плоский сдвиг по подошве фундамента (см. лекцию 1) и глубинный сдвиг в форме вращения по круглоцилиндрической поверхности (рис. 5.9).
При наличии в основании водонасыщенных грунтов в обоих случаях учитывают степень фильтрационной консолидации грунта (см. лекцию 1). Предполагается, что центр круглоцилиндрической поверхности вращения лежит на пересечении внутренней грани стены подвала и нижней плоскости перекрытия над подвалом (рис. 5.9). Радиусом круглоцилиндрической поверхности r является линия, соединяющая центр вращения с крайней точкой подошвы фундамента со стороны наружной стены. Для системы сил, действующих на фундамент и основание на рис. 5.9, коэффициент устойчивости основания от вращения по круглоцилиндрической поверхности представится формулой:

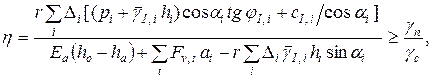 (5.2)
(5.2)
где D i, hi - ширина и высота элементарного объема грунта ниже подошвы фундамента или за ее границами; pi – давление под подошвой фундамента, вызванное действием вертикальных сил Fv, t; `g I, i – средневзвешенный удельный вес грунта в пределах высоты hi; j I, i, cI, i – расчетные значения угла внутреннего трения и сцепления на i–м участке линии скольжения;
a i – острый угол наклона к горизонтали касательной к цилиндрической поверхности в точке i, принимаемый положительным, если поворот горизонтали до совмещения с касательной происходит против хода часовой стрелки; ho - расстояние от центра поворота до подошвы фундамента; Ea, ha – сила активного давления и плечо ее приложения относительно подошвы фундамента; Fv, t, at – вертикальная сила и плечо ее приложения относительно центра поворота О; g n , g c – коэффициент надежности по назначению сооружения (больший единицы) и коэффициент условия работы основания (меньший единицы).
Напряжения под подошвой фундамента pi вычисляются по формуле (5.1) от расчетных усилий N и M, полученных приведением к центральной оси фундаментной плиты сил Fv, t. За пределами подошвы фундамента напряжения pi равны нулю. Вычисления по формуле (5.2) выполняются при наличии и отсутствии пригруза на поверхности основания интенсивностью q. Если условие (5.2) не выполняется, производят увеличение несущей способности основания путем увеличения ширины фундамента и (или) глубины его заложения. Если указанные меры не приводят к должному результату, переходят на другой тип фундамента, например, свайный.
 3.4. Расчет фундаментной плиты. Расчеты выполняют для единичной длины фундаментной плиты в ее поперечном сечении. Плиту рассматривают как консоль, защемленную по грани стены и нагруженную давлением грунта, по аналогии с плитой столбчатого фундамента (см. лекцию 4). По изгибающему моменту в опорном сечении подбирается площадь поперечного сечения арматуры в нижней зоне плиты. Площадь сечения арматуры уточняют по результатам расчетов ширины раскрытия трещин в нижней зоне плиты. Толщину плиты определяют из расчета на поперечную силу. Длину проекции наклонной трещины в опорном сечении (рис. 5.10) принимают h0 и 2×h0, где h0 - толщина плиты за вычетом защитного слоя бетона растянутой арматуры.
3.4. Расчет фундаментной плиты. Расчеты выполняют для единичной длины фундаментной плиты в ее поперечном сечении. Плиту рассматривают как консоль, защемленную по грани стены и нагруженную давлением грунта, по аналогии с плитой столбчатого фундамента (см. лекцию 4). По изгибающему моменту в опорном сечении подбирается площадь поперечного сечения арматуры в нижней зоне плиты. Площадь сечения арматуры уточняют по результатам расчетов ширины раскрытия трещин в нижней зоне плиты. Толщину плиты определяют из расчета на поперечную силу. Длину проекции наклонной трещины в опорном сечении (рис. 5.10) принимают h0 и 2×h0, где h0 - толщина плиты за вычетом защитного слоя бетона растянутой арматуры.
Величина поперечной силы определяется по формуле:
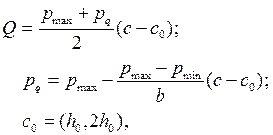 (5.3)
(5.3)
где b – ширина ленточного фундамента; с – длина консоли (расстояние от грани стены до края фундамента).
Прочность наклонного сечения плиты проверяется по формуле:
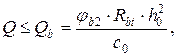 (5.4)
(5.4)
где j b2 – коэффициент, зависящий от вида бетона (для тяжелого бетона равен 2); Rbt – сопротивление бетона растяжению.
При невыполнении условия (5.4) увеличивают толщину плиты или применяют бетон более высокого класса по прочности.

3.5. Расчет стены подвала на действие активного давления грунта. Расчет ведется на единицу длины стены подвала. Активное давление грунта (см. лекцию 4 курса "Механика грунтов") определяется с учетом пригруза на поверхности основания с наружной стороны грунта (рис. 5.11).
Расчетную схему стены подвала принимают в зависимости от конструкции фундамента. Для монолитного фундамента принимают шарнирное опирание на перекрытие над подвалом и жесткое защемление в уровне пола подвала. Для сборного фундамента оба закрепления принимаются шарнирными. Рассматривают три основных сочетания нагрузок, включающих распределенную по трапеции горизонтальную нагрузку от активного давления грунта pa и внецентренно приложенную силу N, равную: в стадии монтажа – нулю; в стадии эксплуатации Nmin = Ng и Nmax = Ng + Np, где Ng и Np – продольные силы соответственно от постоянных и временных нагрузок. По результатам статических расчетов на основные сочетания нагрузок сроят огибающие эпюры изгибающих моментов и поперечных сил (рис. 5.11). Поперечные сечения стены подвала рассчитывают как внецентренно сжатые. По результатам расчетов определяется необходимость вертикального армирования стены подвала и при необходимости назначается величина поперечного сечения продольной арматуры. Поперечные силы должны восприниматься работой материала стены на растяжение по наклонным сечениям.
3.6. Расчет ленточного фундамента в продольном направлении. Необходимость такого расчета возникает, когда ленточный фундамент загружен неравномерно по длине, например, сосредоточенными силами от колонн, или устраивается на неоднородном в плане основании. В этих случаях ленточные фундаменты устраивают, как правило, в виде монолитных или сборно-монолитных систем перекрестных балок или балок – стенок. Такие системы рассчитываются как конструкции на упругом основании (см. лекцию 2). По результатам статических расчетов определяют расчетные усилия в сечениях фундамента (продольные и поперечные силы, изгибающие и крутящие моменты). Из расчета сечений на указанные усилия определяют расчетное армирование элементов и уточняют геометрические размеры сечений и классы материалов по прочности. В стенах и плитах ленточного фундамента устанавливается продольная (горизонтальная) арматура для восприятия изгибающих и крутящих моментов, а также поперечная (вертикальная в стенах и горизонтальная в плитах) арматура для восприятия поперечных сил и крутящих моментов (рис. 5.12). Описанный метод расчета ленточного фундамента является наиболее общим и включает в себя ранее описанные методы как частные инженерные приемы.














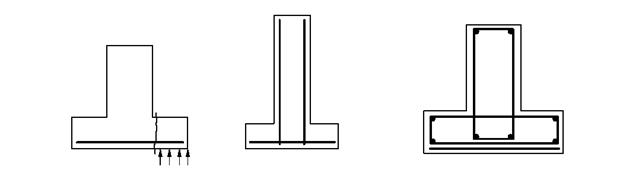
Рис. 5.12. Схемы армирования ленточного фундамента: а – без учёта изгиба в продольном направлении; б – то же с учётом горизонтального давления грунта; в – общий случай; 1 – арматура в балке, обеспечивающая прочность нормальных сечений при действии отпора грунта; 2 – арматура в плите, обеспечивающая прочность нормальных (горизонтальных) сечений при действии горизонтальных нагрузок; 3 – арматура в балке, обеспечивающая прочность её нормальных сечений при изгибе фундамента в продольном направлении; 4 – то же наклонных сечений; 5, 6 – арматура в плите, повышающая прочность фундамента при действии вертикальных усилий.
4. Расчет плитных фундаментов. Плитный фундамент рассчитывается по двум схемам: как абсолютно жесткий фундамент и как фундамент конечной жесткости. Из расчетов по первой схеме определяют размеры фундамента в плане, среднюю осадку и общие крены плиты в продольном и поперечном направлении. Из расчетов по второй схеме определяют внутренние усилия в плитном фундаменте и его осадки в плане.

4.1. Определение размеров плиты в плане. Действующие на плитный фундамент нагрузки приводятся к продольной силе N, действующей в центре плиты, и к изгибающим моментам Mx и My, действующим относительно продольной x и поперечной y осей фундамента (рис. 5.13).
Размеры плиты в плане устанавливаются из условий ограничения средних давлений под плитой и максимальных давлений на средине стороны и в угловой точке подошвы фундамента. Расчеты выполняются по формулам для столбчатого фундамента (см. лекцию 4).
4.2. Расчет средней осадки и кренов плиты. Средние осадки вычисляются от действия обобщенной силы N как для столбчатого фундамента. Расчет осадки выполняется, как правило, по методу линейно деформируемого слоя (см. лекцию 8 курса "Механика грунтов"). Крены вычисляются от действия обобщенных изгибающих моментов Mx и My как для столбчатого фундамента. При этом в расчетах используют осредненные характеристики грунта в пределах сжимаемой толщи под подошвой фундамента (см. лекцию 8 курса "Механика грунтов"). Средние осадки и крены сопоставляют с их допустимыми значениями, приведенными в нормах на проектирование оснований. Если условия по ограничению средней осадки и кренов не выполняются, увеличивают размеры фундамента в плане.
4.3. Расчет фундаментной плиты на продавливание. Как правило, толщина фундаментной плиты определяется из расчетов ее на продавливание в зонах действия сосредоточенных нагрузок от колонн, столбов, стен и т.п. Расчеты на продавливание выполняются по четырем сторонам и по короткой стороне с использованием формул для столбчатого фундамента (см. лекцию 12). Если прочность плиты на продавливание оказывается недостаточной, увеличивают толщину плиты или повышают класс бетона по прочности.
4.4. Расчет плиты по деформированной схеме. Плита рассчитывается как конструкция на упругом основании на действие фактически приложенных нагрузок. Для расчета плит на упругом основании наибольшее распространение в расчетной практике нашел метод конечных элементов. Расчетная схема плиты (рис. 5.14) представляется ансамблем прямоугольных или треугольных конечных элементов.

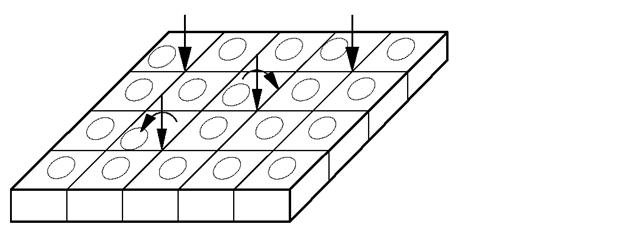
Рис. 5.14. Конечно-элементная расчётная схема плиты с использованием специального типа конечных элементов, взаимодействующих с упругим основанием: 1…30 – номера узлов расчётной схемы; 1 - 20 - номера конечных элементов.
В большинстве прикладных программ имеется тип конечного элемента, взаимодействующего с упругим основанием. Упругое основание характеризуется коэффициентом жесткости (см. лекцию 2). Для вычисления коэффициентов жесткости основания в плане плиты выполняют расчеты по определению осадок в узлах конечных элементов от действия равномерно распределенной нагрузки на плите. Плита в этих расчетах считается абсолютно гибкой. Рекомендуется рассчитывать упругие и пластические осадки основания с целью учета распределительных свойств основания в соответствии с моделью коэффициента жесткости профессора Клепикова (см. лекцию 2). Коэффициенты жесткости в плане плиты определяют делением распределенной нагрузки на найденные значения осадок. Результатом статического расчета плиты как конструкции на упругом основании являются внутренние усилия в ее сечениях (изгибающие и крутящие моменты, поперечные и продольные силы). Расчетом сечений на найденные усилия проверяется их прочность при принятых геометрических размерах, армировании и классах материалов по прочности. По результатам расчетов корректируются конструктивные параметры плитного фундамента. Пример армирования фундаментной плиты по результатам деформационного расчета (рис. 5.15) представлен на рис. 5.16.






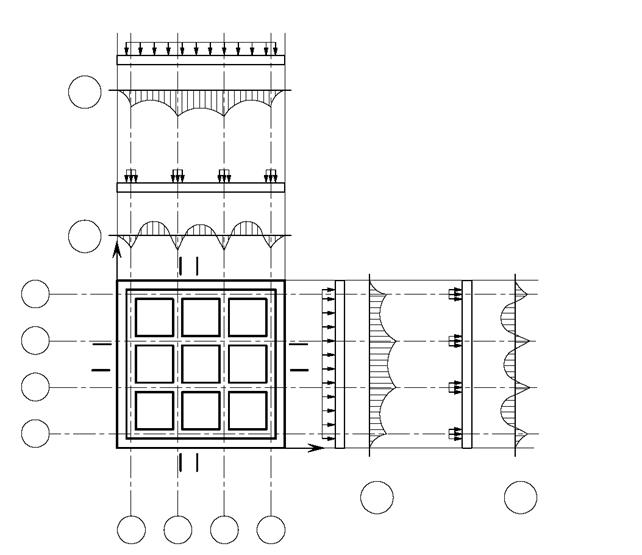
Рис. 5.15. Эпюры изгибающих моментов в сечениях плитного фундамента при действии распределённой по периметру стен нагрузки.


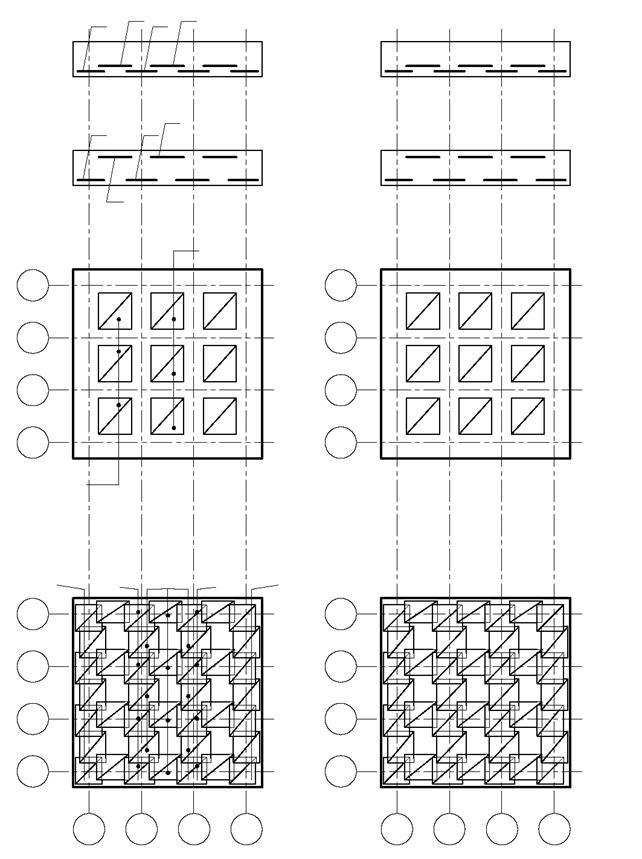
Рис. 5.16. Принципиальные схемы армирования плитного фундамента по эпюрам прогибающих моментов, представленных на рисунке 5.14.: а – армирование вдоль буквенных осей; б – армирование вдоль цифровых осей; С1…С5 – арматурные сетки.
 1. Конструкции ленточных фундаментов. Ленточные фундаменты предназначены для передачи нагрузок на основание от стен. Они также могут использоваться для передачи больших нагрузок от колонн, когда определенные по расчету площади подошвы столбчатых фундаментов сливаются в одну ленту. Ленточный фундамент (рис. 5.1) состоит из фундаментной плиты и из фундаментной балки.
1. Конструкции ленточных фундаментов. Ленточные фундаменты предназначены для передачи нагрузок на основание от стен. Они также могут использоваться для передачи больших нагрузок от колонн, когда определенные по расчету площади подошвы столбчатых фундаментов сливаются в одну ленту. Ленточный фундамент (рис. 5.1) состоит из фундаментной плиты и из фундаментной балки.











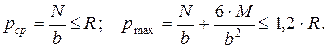 (5.1)
(5.1)
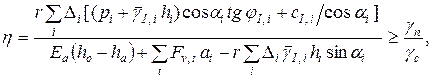 (5.2)
(5.2) 3.4. Расчет фундаментной плиты. Расчеты выполняют для единичной длины фундаментной плиты в ее поперечном сечении. Плиту рассматривают как консоль, защемленную по грани стены и нагруженную давлением грунта, по аналогии с плитой столбчатого фундамента (см. лекцию 4). По изгибающему моменту в опорном сечении подбирается площадь поперечного сечения арматуры в нижней зоне плиты. Площадь сечения арматуры уточняют по результатам расчетов ширины раскрытия трещин в нижней зоне плиты. Толщину плиты определяют из расчета на поперечную силу. Длину проекции наклонной трещины в опорном сечении (рис. 5.10) принимают h0 и 2×h0, где h0 - толщина плиты за вычетом защитного слоя бетона растянутой арматуры.
3.4. Расчет фундаментной плиты. Расчеты выполняют для единичной длины фундаментной плиты в ее поперечном сечении. Плиту рассматривают как консоль, защемленную по грани стены и нагруженную давлением грунта, по аналогии с плитой столбчатого фундамента (см. лекцию 4). По изгибающему моменту в опорном сечении подбирается площадь поперечного сечения арматуры в нижней зоне плиты. Площадь сечения арматуры уточняют по результатам расчетов ширины раскрытия трещин в нижней зоне плиты. Толщину плиты определяют из расчета на поперечную силу. Длину проекции наклонной трещины в опорном сечении (рис. 5.10) принимают h0 и 2×h0, где h0 - толщина плиты за вычетом защитного слоя бетона растянутой арматуры.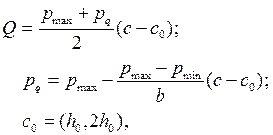 (5.3)
(5.3)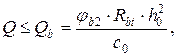 (5.4)
(5.4)



























