(Лекция 02.09.2014)
Геометрическая интерпретация задач линейного программирования
(Лекция 02.09.2014)
Свойства решений задачи линейного программирования
Рассмотрим задачу линейного программирования со смешанными ограничениями:
 ,
,  ; (1)
; (1)
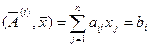 ,
, 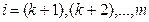 ; (2)
; (2)
кроме того, все переменные должны удовлетворять условиям неотрицательности, то есть:
 ,
, 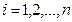 ; (3)
; (3)
Пусть множество этих ограничений непротиворечиво, то есть R≠Æ.
Тогда справедлива следующая теорема:
Теорема 1. Об области определения ЗЛП
Множество R, определяемое совокупностью ограничений (1), (2), является выпуклым замкнутым множеством.
Доказательство
1) Выпуклость множества R следует из теоремы №4 раздела «Выпуклые функции», поскольку множество R удовлетворяет условиям-ограничениям 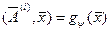 , а эти ограничения сами являются выпуклыми функциями.
, а эти ограничения сами являются выпуклыми функциями.
2) Покажем замкнутость множества R.
Рассмотрим произвольную последовательность точек 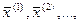 сходящуюся к
сходящуюся к 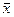 - какой-либо точке множества R, то есть
- какой-либо точке множества R, то есть 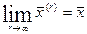 , причем все эти точки принадлежат множеству R.
, причем все эти точки принадлежат множеству R.
Тогда для системы ограничений (1), (2) справедливы выражения для любого r; так как точки 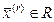
 ,
, 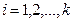 ;
;
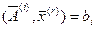 ,
, 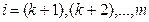 ;
;
Согласно свойству непрерывности скалярного произведения векторов, можно записать:
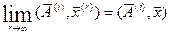 , (4)
, (4)
Если с учетом (4) перейти в этих выражениях к пределу, то получим предельные зависимости:
(--21--)
 ,
, 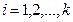 ;
;
 ,
, 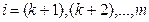 ;
;
Но в качестве точки  может быть выбрана и любая граничная точка
может быть выбрана и любая граничная точка  , так как никаких ограничений на последовательность
, так как никаких ограничений на последовательность 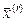 мы не накладывали. Но множество, содержащее все свои граничные точки, является замкнутым. Поэтому, множество R замкнуто.
мы не накладывали. Но множество, содержащее все свои граничные точки, является замкнутым. Поэтому, множество R замкнуто.
Поскольку выражение  задаёт полупространство, а
задаёт полупространство, а 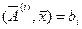 - гиперплоскость, постольку множество планов задачи ЛП, определяемой системой выражений (1),(2) является пересечением, то есть общей частью конечного числа гиперплоскостей и полупространств, которое называется выпуклым многогранным множеством. Если оно ограничено, то такое выпуклое многогранное множество называется выпуклым многогранником.
- гиперплоскость, постольку множество планов задачи ЛП, определяемой системой выражений (1),(2) является пересечением, то есть общей частью конечного числа гиперплоскостей и полупространств, которое называется выпуклым многогранным множеством. Если оно ограничено, то такое выпуклое многогранное множество называется выпуклым многогранником.
Понятие выпуклого многогранника сходно с понятием выпуклой оболочки, то есть выпуклый многогранник представляет собой множество точек вида 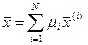 , где
, где 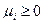 ,
, 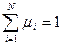 ,
, 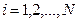 , где
, где 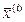 - крайние точки многогранника.
- крайние точки многогранника.
Крайняя точка выпуклого многогранного множества называется вершиной (опорным планом). Такая крайняя точка называется вершиной в том случае, если среди условий (1), (2), (3) найдётся n условий (линейно-независимых), которые для данной точки выполняются как строгие равенства.
Но так как вектор  должен удовлетворять условию неотрицательности, то среди n равенств, соответствующих условиям-ограничениям (1), (2), (3), содержащих m штук линейных зависимостей, может быть взято (n-m) равенств вида
должен удовлетворять условию неотрицательности, то среди n равенств, соответствующих условиям-ограничениям (1), (2), (3), содержащих m штук линейных зависимостей, может быть взято (n-m) равенств вида 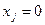 . Такие значения переменных относятся к общему случаю.
. Такие значения переменных относятся к общему случаю.
Но могут встречаться так называемые случаи вырожденности, когда в нуль обращаются больше, чем (n-m) компонентов.
(--22--)
Вершина выпуклого многогранника называется вырожденной в случае, когда число ограничений, которым она удовлетворяет, как точным равенствам, больше n. Иллюстрацией сказанного может служить рисунок, соответствующий решению задачи ЛП на плоскости, когда оптимальному решению соответствует точка А.

Разъяснение: это действительно так, потому что, например, уравнение (1) имеет вид: 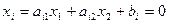 , то есть компоненты
, то есть компоненты 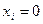 ; то же справедливо в общем случае и для прямых (2), (3).
; то же справедливо в общем случае и для прямых (2), (3).
Поскольку число вершин многогранника конечно, то и количество опорных планов конечно, причем любой план может быть получен как выпуклая линейная комбинация крайних точек многогранника, то есть опорных планов:
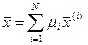 ,
, 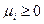 ,
, 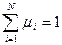 ,
, 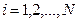 , (5)
, (5)
Иначе говоря, опорные планы представляют собой основу (опорные точки), дающие возможность построить любой допустимый план задачи, поэтому эти точки и названы опорными.
Из теоремы о крайней точке следует, что если область существования решений представляет собой не пустое множество (то есть выпуклое замкнутое ограниченное множество), то существует, по крайней мере, один опорный план.
Теорема 2. Об оптимальности
Линейная форма 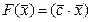 , определённая на выпуклом многограннике
, определённая на выпуклом многограннике  ,
, 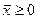 , достигает своего экстремума в вершине этого многогранника.
, достигает своего экстремума в вершине этого многогранника.
Доказательство
Пусть 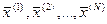 - все вершины многогранника Х, на котором линейная форма определена, и
- все вершины многогранника Х, на котором линейная форма определена, и  - точка многогранника, в которой линейная форма достигает своего минимума, то есть
- точка многогранника, в которой линейная форма достигает своего минимума, то есть 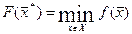 .
.
Согласно (5) можно записать:  ,
, 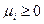 ,
, 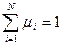 ,
, 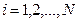 ,
,
(--23--)
и 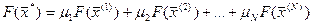 . (так, как линейная форма является выпуклой и вогнутой одновременно)
. (так, как линейная форма является выпуклой и вогнутой одновременно)
Выберем наименьшее из  . Тогда пусть это
. Тогда пусть это 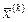 .
.
 .
.
Но поскольку 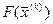 есть наименьшее значение линейной формы, то
есть наименьшее значение линейной формы, то 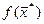 должно совпадать с
должно совпадать с 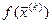 , то есть
, то есть  может быть в том числе вершиной выпуклого многогранника.
может быть в том числе вершиной выпуклого многогранника.
Вопрос о существовании оптимального плана решается с помощью
Теоремы 3.О разрешимости.
Для того, чтобы задача ЛП была разрешимой, то есть существовал оптимальный план, необходимо и достаточно выполнения двух условий:
А. множество планов задачи непусто.
Б. линейная форма ограничена на этом множестве сверху (для задачи максимизации) или снизу (для задачи минимизации).
(--24--)
В заключение рассмотрения общих свойств задач ЛП можно сделать следующие выводы:
1) непустое множество планов задачи имеет конечное число опорных планов,
2) любая разрешимая задача имеет оптимальное решение среди опорных планов и может быть найдено за конечное число шагов,
3) множество точек, в которых линейная форма имеет постоянное значение, есть гиперплоскость, и гиперплоскости, соответствующие разным значениям линейной формы, параллельны между собой,
4) локальный экстремум является одновременно и глобальным экстремумом линейной формы на множестве планов задачи.
Двойственные задачи линейного программирования
Каждой задаче ЛП можно поставить в соответствие другую задачу ЛП, которую называют двойственной по отношению к первой задаче. Целью данного параграфа является изложение вопросов, характеризующих неотъемлемую связь этих задач (прямой и двойственной).
Пусть прямая задача записана в общем виде:
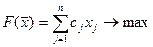 ; (1)
; (1)
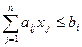 ,
, 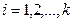 ; (2)
; (2)
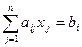 ,
,  ; (3)
; (3)
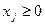 ,
, 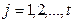 ,
, 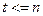 . (4)
. (4)
(--25--)
Двойственная задача, или задача, сопряжённая с данной, тогда должна записываться так:
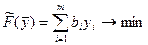 ; (5)
; (5)
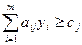 ,
, 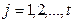 ;
; 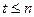 (6)
(6)
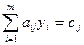 ,
, 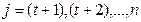 ; (7)
; (7)
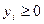 ,
,  ,
, 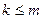 (8)
(8)
Другими словами, двойственная задача образуется по следующим правилам:
1) вид экстремума меняется на противоположный,
2) векторы 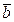 и
и 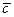 меняются местами (вектор линейной формы прямой задачи становится вектором ограничений двойственной задачи, а вектор ограничений прямой задачи становится вектором линейной формы двойственной задачи),
меняются местами (вектор линейной формы прямой задачи становится вектором ограничений двойственной задачи, а вектор ограничений прямой задачи становится вектором линейной формы двойственной задачи),
3) матрица условий 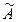 двойственной задачи образуется транспонированием матрицы А прямой задачи, то есть
двойственной задачи образуется транспонированием матрицы А прямой задачи, то есть 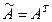 ,
,
4) j-ое условие двойственной задачи будет неравенством, если на j-ую переменную прямой задачи наложено требование неотрицательности, в противоположном случае j-ое условие будет равенством,
5) на i-ую переменную двойственной задачи должно быть наложено условие неотрицательности, если i-ое условие прямой задачи является неравенством.
Для канонической формы записи прямой задачи двойственная по отношению к ней задача записывается следующим образом:
 , ,
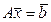 , ,

| 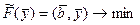 , ,

|
| Прямая задача (9) | Двойственная задача (10) |
(--26--)
Пример прямой и двойственной к ней задачи:
Пусть прямая задача формулируется в виде:
Изготовление изделий двух видов И1 и И2 требует затрат четырёх видов сырья р1, р2, р3, р4, запасы которых соответственно ограничены значениями b1, b2, b3, b4 единиц.
Количество единиц сырья, необходимое для выпуска каждого из изделий, задано таблицей 1 (там же в нижней строке приведены величины дохода, получаемого выпускающим предприятием, при реализации каждого из изделий).
Математическая модель этой задачи такова:
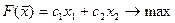
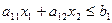

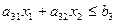
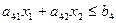
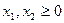
|
|
Формулировка двойственной задачи ЛП
Пусть при тех же условиях существуют дополнительные: другую организацию интересует, за какую общую минимальную цену можно купить всё сырье у организации, выпускающей изделия И1 и И2; ясно, что выпускающая организация не продаст сырье, если покупатель заплатит за единицу каждого сырья цену, меньшую, чем та, которую выпускающая организация получит, изготовив изделия из этого же сырья.
Пусть у1, у2, у3, у4 – цена единицы сырья р1, р2, р3, р4, тогда математическая модель двойственной задачи будет иметь вид:
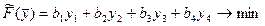
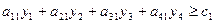
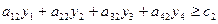

Переменные уi называют оценками или учётными (неявными) ценами.
(--27--)
Связь между прямой и двойственной к ней задачами (то есть между задачами двойственной пары) является не только внешней, но и глубоко внутренней, о чем позволяет сделать заключение следующий ряд лемм и теорем.
Лемма 1
Если 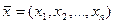 и
и 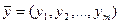 являются произвольными допустимыми планами задач (9), (10), то функции цели этих задач связаны неравенством
являются произвольными допустимыми планами задач (9), (10), то функции цели этих задач связаны неравенством
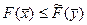
Доказательство
Из выражения (10) следует, что 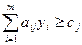 ,
, 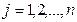 , следовательно:
, следовательно:
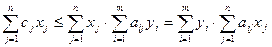
Но по условию (9) выражение 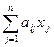 равно соответствующему ему
равно соответствующему ему  . Значит:
. Значит:
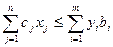
ч.т.д.
Лемма 2
Если для некоторых планов 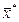 и
и 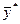 задач (9) и (10) имеет место равенство значений функций цели, то есть
задач (9) и (10) имеет место равенство значений функций цели, то есть
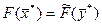 (11)
(11)
то планы 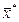 и
и 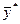 являются оптимальными.
являются оптимальными.
Доказательство
По лемме 1 можно записать 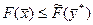 для любых планов
для любых планов 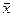 и
и 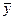
Но по условию леммы 2:  , подставляя это выражение в правую часть предыдущего неравенства, получим доказательство оптимальности плана
, подставляя это выражение в правую часть предыдущего неравенства, получим доказательство оптимальности плана 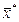 , т.к. будет:
, т.к. будет:
 , ч.т.д.
, ч.т.д.
По лемме 1 можно записать 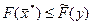 .
.
Подставляя в это неравенство 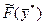 вместо
вместо 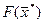 , получим:
, получим: 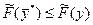 , ч.т.д., так как доказывает оптимальность плана
, ч.т.д., так как доказывает оптимальность плана 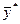
(--28--)
Лемма 3
Если линейная форма 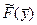 двойственной задачи (10) не ограничена снизу на множестве своих планов, то прямая задача (9) не имеет ни одного плана.
двойственной задачи (10) не ограничена снизу на множестве своих планов, то прямая задача (9) не имеет ни одного плана.
Доказательство
Из условия системы следует, что существует такая последовательность планов 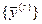 двойственной задачи (10), что
двойственной задачи (10), что
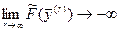
Предположим, что прямая задача (9) имеет некоторый план 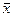 .
.
Тогда по лемме 1:  , т.е. переходим к пределу:
, т.е. переходим к пределу: 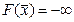 , то есть мы пришли к противоречию, так как при любом плане
, то есть мы пришли к противоречию, так как при любом плане 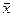 (с конечными составляющими) это равенство невозможно. Следовательно, в этом случае множество планов прямой задачи пусто, ч.т.д.
(с конечными составляющими) это равенство невозможно. Следовательно, в этом случае множество планов прямой задачи пусто, ч.т.д.
Основные свойства задач двойственной пары можно сформулировать в виде двух теорем:
Теорема1 (первая теорема двойственности)
Если одна из задач двойственной пары имеет оптимальное решение, то другая задача также разрешима. При этом для любых оптимальных планов 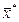 и
и 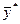 имеет место равенство:
имеет место равенство:
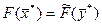
(--29--)
Следствие 1
Для разрешимости одной из задач двойственной пары необходимо и достаточно, чтобы каждая из задач имела хотя бы один план.
Следствие 2
Для того, чтобы одна из задач двойственной пары имела планы, а множество планов другой задачи было пусто, необходима и достаточна неограниченность функции цели первой задачи на множестве её планов.
Следствие 3
Для оптимальных планов 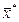 и
и 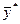 задач двойственной пары необходимо и достаточно выполнение равенства
задач двойственной пары необходимо и достаточно выполнение равенства 
Теорема 2 (вторая теорема двойственности)
Пусть обе задачи двойственной пары разрешимы (1)-(4) и (5)-(8).
Если оптимальный план одной из задач обращает i-ое ограничение этой задачи в строгое неравенство, то i-ая компонента оптимального плана другой задачи равна нулю.
Если же i-а компонента оптимального плана одной задачи положительна, то оптимальный план двойственной задачи обращает i-ое ограничено в строгое равенство.
То есть выполняются условия дополняющей нежёсткости:
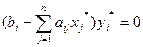 ,
, 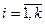
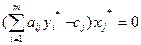 ,
, 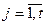
Тема 3. Методы решения общей задачи ЛП
Идея метода последовательного улучшения плана, признак оптимальности
(--30--)
Метод последовательного улучшения плана (симплекс-метод)
За рубежом этот метод называется симплексным, но, принимая во внимание, что такое название не отражает сущности метода, название, принятое в отечественной литературе, является более удачным.
Симплекс – это многогранник в n-мерном пространстве, заданный следующими уравнениями:
 ,
, 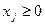 ,
, 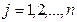
Идея метода последовательного улучшения плана
В подавляющем большинстве случаев в задачах линейного программирования число ограничений меньше числа неизвестных, то есть m<n.
Но даже в этих случаях мы не можем быть уверены, что существует решение, которое удовлетворяет всем условиям неотрицательности переменных.
Прежде чем приступать к непосредственному рассмотрению метода последовательного улучшения плана, сформулируем несколько понятий:
Решением задачи ЛП назовём такой набор значений переменных 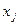 , который удовлетворяет всем ограничениям задачи, за исключением, быть может, ограничений, накладываемых на знак самих переменных.
, который удовлетворяет всем ограничениям задачи, за исключением, быть может, ограничений, накладываемых на знак самих переменных.
Допустимым решением назовём решение с неотрицательными значениями переменных 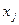 .
.
Базисом называется набор из m переменных, (по числу ограничений задачи ЛП), которые выражены через остальные переменные. Эти m переменных называются базисными переменными, а остальные переменные – небазисными переменными.
(--31--)
Базисное решение – такое решение, в котором всем небазисным переменным присваиваются нулевые значения, а значения базисных переменных вычисляются.
Допустимым базисным решением называется такое базисное решение, которое одновременно является и допустимым.
Опираясь на эти определения, можно кратко охарактеризовать идею метода последовательного улучшения плана.
Сначала находим допустимое базисное решение, которое совпадает с вершиной выпуклого многогранного множества (по определению вершины); определяем, является ли это решение оптимальным или нет. Если нет, то выводим (вычеркиваем) из базиса один вектор и заменяем его другим вектором, получая таким образом новый базис. Его так же исследуем на оптимальность. Поскольку количество вершин многогранного множества конечно, то и подобный процесс конечен, и в результате его либо находится экстремум, либо доказывается несовместность ограничений (противоречивость их), либо доказывается неограниченность функции цели снизу (если решается задача минимизации) или сверху (если решается задача максимизации).
Пусть задача линейного программирования задана в каноническом виде:
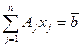 , где (1)
, где (1)
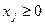 ,
, 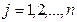 (2)
(2)
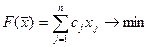 (3)
(3)
где 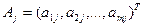 - вектор, состоящий из элементов j-го столбца матрицы А.
- вектор, состоящий из элементов j-го столбца матрицы А.
(--32--)
В общем случае будем предполагать, что ранг матрицы А равен m, то есть r=m.
Рангом матрицы называется наибольший из порядков отличных от нуля миноров, сформированных из элементов матрицы А с сохранением их взаимного расположения.
Предположим, что нам известно допустимое базисное решение (опорный план) задачи, то есть задан набор базисных переменных: 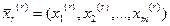 , где индекс r просто указывает на принадлежность данного параметра базису. Соответственно, задан и базисный набор векторов
, где индекс r просто указывает на принадлежность данного параметра базису. Соответственно, задан и базисный набор векторов 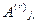 , составляющих базис векторов:
, составляющих базис векторов: 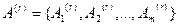 .
.
В этом случае произвольный вектор условий 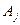 может быть разложен по базису
может быть разложен по базису 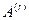 :
:
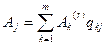 ,
, 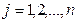 ,
,
где 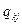 - составляющая разложения векторов
- составляющая разложения векторов 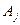 по векторам базиса при векторе
по векторам базиса при векторе 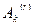 , находящемся в k-ой позиции базиса.
, находящемся в k-ой позиции базиса.
Подобной же операции можно подвергнуть и вектор 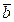 , то есть:
, то есть:
 , где индекс 0 показывает, что эти составляющие расположены в столбце, соответствующем вектору ограничений.
, где индекс 0 показывает, что эти составляющие расположены в столбце, соответствующем вектору ограничений.
То есть можно записать общую формулу:
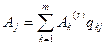 ,
,  (4)
(4)
Кроме того, при подобном разложении всех векторов функция цели приобретет вид:
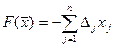 ,
, 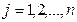 , где
, где
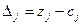 ,
, 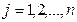 (5)
(5)
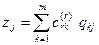 ,
,  , (6)
, (6)
где индекс rk коэффициента с указывает, что это коэффициент с при базисной переменной 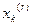 .
.
(--33--)
Все эти параметры однозначным образом определяются при выборе того или иного базиса. Используя параметры 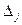 , можно сформулировать признак оптимальности допустимого базисного решения в виде теоремы:
, можно сформулировать признак оптимальности допустимого базисного решения в виде теоремы:
Теорема (признак оптимальности)
Допустимое базисное решение 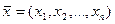 является оптимальным, если
является оптимальным, если  для всех
для всех 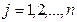 .
.
Доказательство
Обозначим символом 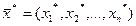 опорный план, для которого выполняется:
опорный план, для которого выполняется:
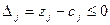 , то есть
, то есть 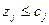 (7)
(7)
А символом 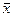 обозначим произвольный опорный план, не совпадающий с планом
обозначим произвольный опорный план, не совпадающий с планом 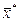 .
.
Будем исследовать произвольный опорный план. Для него должны выполняться условия (1), (2); причём условие (1) запишем в несколько другой форме, воспользовавшись выражением (4) для разложения векторов 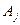 по векторам базиса опорного плана
по векторам базиса опорного плана 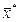 . В этом случае получим:
. В этом случае получим:
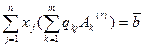 , или в другом виде:
, или в другом виде:
 (8)
(8)
Но план 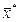 также удовлетворяет условиям (1), поэтому можно записать:
также удовлетворяет условиям (1), поэтому можно записать:
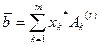 (9)
(9)
(Поскольку это допустимое базисное решение, то есть все небазисные решения =0)
Сравниваем (8) и (9), делаем вывод, что:
 (10)
(10)
Используя выражения (6), (7), (10), можно записать применительно к плану 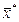 :
: 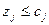 (по условию теоремы) при
(по условию теоремы) при 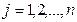 . Помножим обе части неравенства на
. Помножим обе части неравенства на 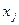 ,
, 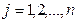 и сложим по всем
и сложим по всем  , тогда слева получим
, тогда слева получим 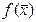 для произвольного плана ЗЛП (какой-либо), а справа произведём перегруппировку слагаемых.
для произвольного плана ЗЛП (какой-либо), а справа произведём перегруппировку слагаемых.
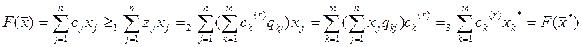
неравенство 1) следует из выражения (7), равенство 2) – из выражения (6) и равенство 3) – из выражения (10).
Следовательно, план 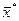 , при котором выполняются условия (7), является оптимальным, так как при любом другом плане
, при котором выполняются условия (7), является оптимальным, так как при любом другом плане 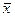 выполняется неравенство
выполняется неравенство 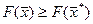 .
.
Дата: 2019-03-05, просмотров: 327.