Постановка задачи

заданы множество Х и функция 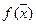, определённая на Х. Требуется найти точки минимума или максимума функции  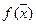на Х. Будем записывать задачу на минимум в виде:

, .

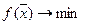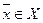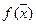 называется целевой функцией (или критерием качества, критериальной функцией).

Х называется допустимым множеством (или решением, планом).

Любой 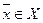 называется допустимой точкой задачи.

Считается, что 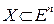, то есть задача является конечномерной.

Точка 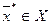 называется точкой глобального минимума функции  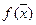на множестве Х (или глобальным решением задачи), если  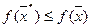при всех .

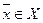Точка 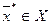 называется точкой локального минимума функции  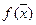на множестве Х (или локальным решением задачи), если существует число ε>0 такое, что

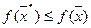 при всех ,

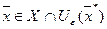где 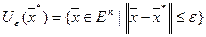 - шар радиуса ε>0 с центром в .

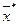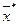Если указанные выше неравенства строгие при , то  называется точкой строгого минимума, то есть строгим решением в глобальном или локальном смысле.

Итак, понятно, что ,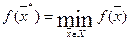

                             ,

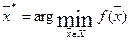то есть точка 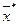 реализует величину .

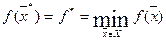Множество всех точек глобального минимума 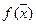 на X обозначается через

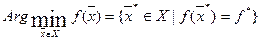
то есть .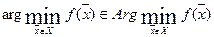

Аналогично для задачи максимизации записываем , .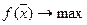

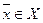Ясно, что такая задача эквивалентна задаче 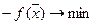,  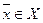в случае совпадения множеств глобальных и локальных решений этих задач.

(--14--)

Для задач оптимизации вопрос о существовании решения решает теорема Вейерштрасса (из математического анализа):

Пусть Х – замкнутое ограниченное множество в Еⁿ. 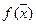 - непрерывная функция на Х. Тогда точка глобального минимума функции  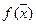на Х существует.

Выделим наиболее важные для теории и приложений объекты оптимизации: реальные, модельные и математические.

1) реальные:

Объект оптимизации представляет собой реальный объект, на котором решается задача оптимизации. Необходимо, однако, чтобы характеристики объекта изменялись значительно медленнее, чем происходит процесс оптимизации, иначе это будет экстремальное регулирование. Например: отладка технического процесса, отработка конструкции.

2) модельные:

обычно в процессе оптимального проектирования объекта задачу оптимизации решают на какой-нибудь физической модели объекта, например, на электронной модели, на цифровой модели на ЭВМ. Критерий качества и состояния ограничений объекта определяются на этой модели.

3) математические

математические объекты, для которых критериальная функция и множество Х заданы математическими выражениями.

Весь процесс оптимального проектирования проходит все три стадии: в), б), а).

В нашем курсе мы подробно остановимся на стадии в).

Сначала выделим наиболее важные классы оптимизационных задач.

(--15--)