1.1.1. Поиск безусловного экстремума
1. Методы одномерного поиска
· Без использования производных
· С использованием производных
2. Методы многомерного поиска
· Без использования производных
· С использованием производных
· Методы сопряженных направлений
3. Методы случайного поиска
1.1.2. Поиск условного экстремума
1. Методы математического программирования
· Методы линейного программирования
· Методы нелинейного программирования
· Методы дробно-линейного программирования
· Методы сепарабельного программирования
· Методы штрафных и барьерных функций
· Методы возможных направлений и градиентные методы
· Методы целочисленного программирования
· Методы стохастического программирования
2. Вариационное исчисление и принцип максимума
3. Динамическое программирование
4. Методы случайного поиска
1.1.3. Поиск экстемумов функций, вычисляемых со случайной ошибкой
1. Метод стохастической аппроксимации
2. Метод планирования экспериментов
Нахождение глобального экстремума
· Вариационное исчисление
· Принцип максимума
· Динамическое программирование
· Человеко-машинные методы
2. Нахождение экстремумов функционалов 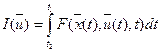
· Вариационное исчисление
· Принцип максимума
· Динамическое программирование
· Человеко-машинные методы
(--3--)
Выпуклые множества
Рассмотрим набор из произвольных векторов из Еn: 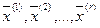 и составим линейную комбинацию векторов с весами mi, i=1,2,…,r:
и составим линейную комбинацию векторов с весами mi, i=1,2,…,r:
 (1)
(1)
При этом, если 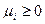 и
и 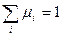 , i=1,2,…,r, то выражение (1) называется выпуклой линейной комбинацией.
, i=1,2,…,r, то выражение (1) называется выпуклой линейной комбинацией.
В свою очередь, множество  (содержащееся) называется выпуклым, если вместе с любыми своими двум точками
(содержащееся) называется выпуклым, если вместе с любыми своими двум точками  оно содержит и любую выпуклую линейную комбинацию вида:
оно содержит и любую выпуклую линейную комбинацию вида:
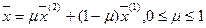 (2)
(2)
Другими словами, множество выпукло, если вместе с любыми двумя своими точками оно содержит и соединяющий их отрезок.
Примеры выпуклых множеств:
Множества, для которых условие (2) не выполняется, являются невыпуклыми:

Из определения выпуклого множества следует, что, если оно содержит более одного элемента, то оно содержит бесконечное число элементов (отрезок состоит из бесконечного числа точек).
Важное свойство выпуклого множества:
Любая выпуклая линейная комбинация произвольного числа точек выпуклого множества также принадлежит этому множеству.
Докажем это:
Пусть 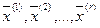 - векторы выпуклого множества G.
- векторы выпуклого множества G.
Образуем из них выпуклую линейную комбинацию:
 , при
, при 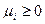 и
и 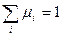
Преобразуем это выражение:

(--4--)
Но выражение в скобках есть не что иное, как выпуклая линейная комбинация двух векторов, принадлежащих ( 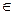 ) G, и, следовательно, также принадлежит G. Обозначив его через
) G, и, следовательно, также принадлежит G. Обозначив его через 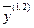 , получим
, получим  , то есть число векторов в этой линейной комбинации сократилось на единицу. Объединив вектор
, то есть число векторов в этой линейной комбинации сократилось на единицу. Объединив вектор 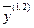 с вектором
с вектором 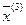 , сокращаем число учитываемых в дальнейшем векторов ещё на единицу. Продолжая таким образом, придём к выражению:
, сокращаем число учитываемых в дальнейшем векторов ещё на единицу. Продолжая таким образом, придём к выражению:
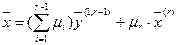 , но поскольку
, но поскольку 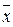 является линейной комбинацией векторов
является линейной комбинацией векторов 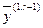 и
и 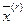 , принадлежащих множеству G, то и сам вектор
, принадлежащих множеству G, то и сам вектор 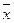 принадлежит этому множеству G, то есть
принадлежит этому множеству G, то есть 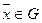 , ч.т.д.
, ч.т.д.
Можно показать, что общая часть (пересечение) произвольного числа выпуклых множеств есть выпуклое множество.
Для доказательства целесообразно рассмотреть чертёж множества G, являющегося пересечением двух выпуклых множеств G1 и G2.
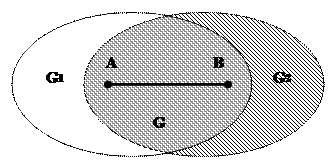
Точки А и В принадлежат одновременно обоим выпуклым множествам G1 и G2, значит и весь отрезок АВ принадлежит G1 и G2 одновременно, следовательно, и их общей части также принадлежит.
Следовательно, доказано, что множество G – выпукло.
Множество точек 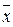 , удовлетворяющих неравенству
, удовлетворяющих неравенству 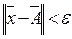 , называется ε‑окрестностью точки
, называется ε‑окрестностью точки 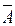 .
.
Если же множество G содержит не только данную (какую-либо) точку, но и её ε‑окрестность, то такую точку называют внутренней точкой множества G.
Если точка 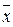 принадлежит G и в её ε‑окрестности есть точки, принадлежащие G и не принадлежащие ему, то такая точка называется граничной.
принадлежит G и в её ε‑окрестности есть точки, принадлежащие G и не принадлежащие ему, то такая точка называется граничной.
(--5--)
Множество, содержащее все свои граничные точки, называется замкнутым, а множество, не содержащее ни одной своей граничной точки, называется открытым (например, ε‑окрестность какой-либо точки, внутренность любого тела без учёта поверхности).
Множество будет обладать свойством связности, если любая его точка имеет ε‑окрестность. Пример несвязного множества – множество точек, координаты которых являются целыми числами.
Множество G называется ограниченным, если для всех его точек 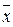 найдётся такое число С, не зависящее от
найдётся такое число С, не зависящее от 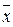 , что
, что 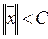 (длина, норма, метрика)
(длина, норма, метрика)
Для евклидова пространства размерности n справедлива теорема Больцано‑Вейрштрасса:
Из любой ограниченной бесконечной последовательности точек En может быть выделена сходящаяся последовательность.
(--6--)
Точка 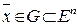 ( Î - принадлежит,
( Î - принадлежит, 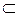 - содержащееся в Rn , т.е. подмножество) называется крайней точкой множества, если не существует двух различных точек
- содержащееся в Rn , т.е. подмножество) называется крайней точкой множества, если не существует двух различных точек 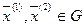 , таких, чтобы для
, таких, чтобы для 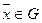 выполнялось
выполнялось 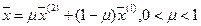 , т.е. в любом взятом отрезке
, т.е. в любом взятом отрезке 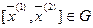 точка
точка 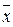 либо не содержится, либо является одним из его концов.
либо не содержится, либо является одним из его концов.
Примеры выпуклых множеств с конечным и бесконечным числом крайних точек:

A, B, C, D, E являются крайними, М не является крайней.

Бесконечное множество крайних точек

На прямой и плоскости не существует крайних точек.
Теорема о крайней точке
Всякое замкнутое выпуклое ограниченное множество G содержит хотя бы одну крайнюю точку.
(--7--)
Множество точек 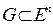 , удовлетворяющих линейному уравнению вида
, удовлетворяющих линейному уравнению вида
 , называется гиперплоскостью..(
, называется гиперплоскостью..( 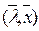 - скалярное произведение)
- скалярное произведение)
По обе стороны от гиперплоскости лежат два множества, называемые полупространствами:
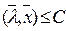 и
и 
Гиперплоскость строго разделяет два множества G1 и G2, если имеют место строгие неравенства:
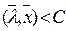 для
для 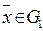
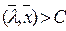 для
для 
Если подобные строгие неравенства не соблюдаются, то множества G1 и G2 считаются просто (нестрого) разделимыми.
Теорема о разделяющей гиперплоскости (фундаментальная теорема)
Пусть G1 и G2 – произвольные выпуклые замкнутые множества без общих точек, из которых хотя бы одно ограничено. Тогда существует гиперплоскость, строго разделяющая множества G1 и G2.
Теорема не верна, если хоть одно из предположений относительно G1 и G2 не соблюдается:

|

| 
|

| ||||
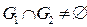
| G1 - невыпуклое | G1 – (1) незамкнутое (2) нет строгого разделения | G1 и G2 неограниченны (в бесконечности получится нестрогое разделение) |
(--8--)
Гиперплоскость 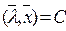 называется опорной к множеству G в точке
называется опорной к множеству G в точке 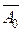 , если:
, если:
1. 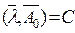 , то есть гиперплоскость содержит точку
, то есть гиперплоскость содержит точку 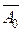 ,
,
2. 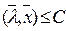 или
или  при
при 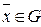 , то есть множество G лежит в одном из полупространств, порождаемых гиперплоскостью.
, то есть множество G лежит в одном из полупространств, порождаемых гиперплоскостью.
Например, если 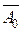 - граничная точка выпуклого замкнутого множества G, то существует опорная гиперплоскость к этому множеству в точке
- граничная точка выпуклого замкнутого множества G, то существует опорная гиперплоскость к этому множеству в точке 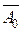 .
.
Выпуклой оболочкой множества 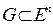 называется множество [G], состоящее из точек вида
называется множество [G], состоящее из точек вида 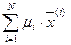 (то есть выпуклая линейная комбинация конечного числа точек множества G , которое может быть и невыпуклым), где
(то есть выпуклая линейная комбинация конечного числа точек множества G , которое может быть и невыпуклым), где  ,
, 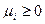 , i=1,2,…,N,
, i=1,2,…,N, 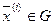 .
.
Выпуклая оболочка является наименьшим из выпуклых множеств, включающих в себя множество G; например:

Укажем некоторые свойства выпуклых оболочек:
1. Выпуклая оболочка произвольного множества есть выпуклое множество.
2. В выпуклую оболочку множества G входит само множество G.
3. Выпуклая оболочка [G] выпуклого множества G совпадает с множеством G, то есть [G]=G.
Если G – выпуклое замкнутое ограниченное множество, а G1 – множество его крайних точек, то G является выпуклой оболочкой множества G1.
(--9--)
Выпуклые функции
Функция 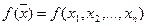 , заданная на выпуклом множестве
, заданная на выпуклом множестве 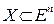 называется выпуклой, если для любых двух точек
называется выпуклой, если для любых двух точек 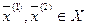 и любого
и любого 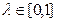 справедливо неравенство
справедливо неравенство
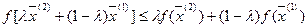 (1)
(1)
(в правой части линейная функция, интерполирующая реальную функцию)
Если при тех де условиях удовлетворяется неравенство:
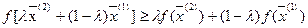 (2)
(2)
(в 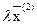 именно больший индекс)
именно больший индекс)
то такая функция называется вогнутой.
Если неравенства превращаются в строгие равенства, то говорят, что функция строго выпукла (строго вогнута).

| 
|
| То есть гиперповерхность выпукла, если отрезок, соединяющий любые две её точки, лежит на поверхности или выше её. | Присутствие условия:
множество  выпукло обязательно, т.к. точка выпукло обязательно, т.к. точка 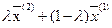 принадлежит множеству тому же только в случае выпуклости его, разумеется при принадлежит множеству тому же только в случае выпуклости его, разумеется при  . .
|
Линейная функция n переменных 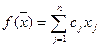 или
или 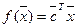 , где
, где 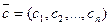 ,
, 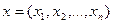 , называется линейной формой.
, называется линейной формой.
Рассмотрим некоторые важные свойства выпуклых функций.
Теорема 1.
Линейная форма 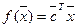 является выпуклой (и вогнутой одновременно) на всём En.
является выпуклой (и вогнутой одновременно) на всём En.
Доказательство
Для любых двух точек 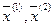 выполняется равенство
выполняется равенство  ,
,  , что и указывает, согласно (1) и (2), на принадлежность
, что и указывает, согласно (1) и (2), на принадлежность  классу выпуклых (вогнутых) функций, но не классу строго выпуклых (вогнутых) функций.
классу выпуклых (вогнутых) функций, но не классу строго выпуклых (вогнутых) функций.
(--10--)
Теорема 2
Если функции 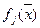 , j=1,2,…,m являются выпуклыми на некотором выпуклом множестве
, j=1,2,…,m являются выпуклыми на некотором выпуклом множестве 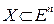 , то функция
, то функция 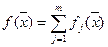 также является выпуклой.
также является выпуклой.
Доказательство:
для любых двух точек 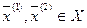 и любого
и любого 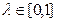 выполняется:
выполняется:
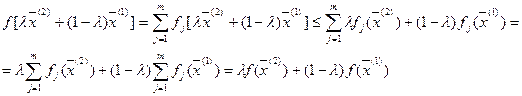
(Неравенство справедливо, т.к. выполняется для любой выпуклой функции)
ч.т.д.
То есть, сумма выпуклых функций есть выпуклая функция.
Теорема 3
Если  выпуклая дифференцируемая функция, то справедливо неравенство:
выпуклая дифференцируемая функция, то справедливо неравенство:
 , где
, где 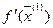 - вектор-градиент функции
- вектор-градиент функции 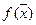 в точке
в точке 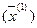 .
.
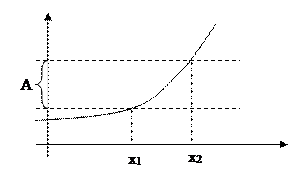
| 
|
A= 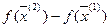
|
Для справки:
Если f(x) – действительная функция, имеющая в интервале 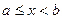 n-ую производную f(n)(x), тогда
n-ую производную f(n)(x), тогда 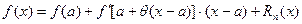 , где
, где 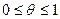 .
.
Доказательство
Из формулы (1) следует, что при всех 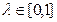
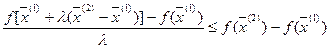
Если разложить числитель этой дроби по формуле Тейлора без учёта остаточных членов выше первого порядка малости, получим:
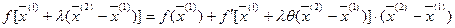 , где
, где 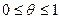 , и переходя к пределу при
, и переходя к пределу при 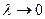 , окончательно получим:
, окончательно получим:
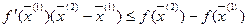 , где
, где 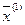 - любая внутренняя точка из множества Х, и
- любая внутренняя точка из множества Х, и 
ч.т.д.
(--11--)
Требование дифференцируемости в теореме нужно, т.к. выпуклая или вогнутая функция не всегда обязательно дифференцируема, например, в точке x1 функция f(x) не имеет производной.

Теорема 4
Если 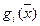 - выпуклые функции и
- выпуклые функции и 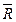 - множество точек, удовлетворяющих условиям
- множество точек, удовлетворяющих условиям
 ,
, 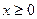 , i=1,2,…,m (*)
, i=1,2,…,m (*)
тогда 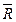 - выпуклое множество.
- выпуклое множество.
Доказательство:
Пусть 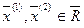 . Рассмотрим точку
. Рассмотрим точку 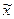 , представляющую собой линейную выпуклую комбинацию
, представляющую собой линейную выпуклую комбинацию 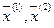 :
: 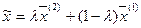 ,
, 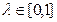 . Теорема будет доказана в том случае, если удастся показать, что
. Теорема будет доказана в том случае, если удастся показать, что  , а в этом случае
, а в этом случае 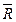 выпукло, так как вместе с любыми двумя своими точками содержит и выпуклую линейную комбинацию этих точек.
выпукло, так как вместе с любыми двумя своими точками содержит и выпуклую линейную комбинацию этих точек.
Очевидно, что 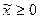 . Осталось показать, что
. Осталось показать, что 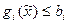 , а это видно из выпуклости
, а это видно из выпуклости  .
.
Действительно:
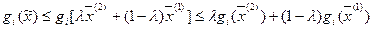 .
.
Из условий (*) следует, что при 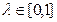 справедливы условия
справедливы условия
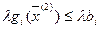 ,
, 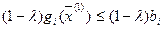
Следовательно:
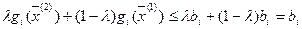 , то есть
, то есть 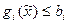 , то есть
, то есть 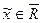 и
и  - выпуклое множество.
- выпуклое множество.
ч.т.д.
(--12--)
Теорема 5
Если 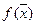 - выпуклая функция, заданная на замкнутом выпуклом множестве
- выпуклая функция, заданная на замкнутом выпуклом множестве 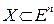 , тогда любой относительный (локальный, местный) минимум
, тогда любой относительный (локальный, местный) минимум 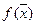 на Х является абсолютным (глобальным) минимумом
на Х является абсолютным (глобальным) минимумом 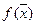 на Х.
на Х.
Доказательство ведём методом от противного.
Предположим, что наряду с относительным минимумом в точке 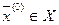 функция
функция 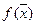 имеет абсолютный минимум в точке
имеет абсолютный минимум в точке 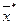 , такой, что
, такой, что 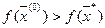
Из условия выпуклости функции следует, что для любого 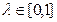 выполняется неравенство:
выполняется неравенство:
 .
.
Если учесть, что 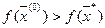 , то можно записать:
, то можно записать:
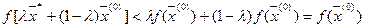
Рассмотрим любую ε‑окрестность точки 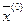 с
с  . Если взять λ такое, что
. Если взять λ такое, что  , то точка
, то точка  лежит в ε‑окрестности точки
лежит в ε‑окрестности точки 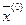 и
и 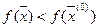 . Но это невозможно, так как
. Но это невозможно, так как 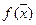 достигает в точке
достигает в точке 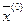 относительного минимума. Таким, образом, любой относительный минимум является одновременно глобальным минимумом для функции
относительного минимума. Таким, образом, любой относительный минимум является одновременно глобальным минимумом для функции 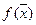 .
.
Если же 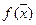 строго выпукла, то абсолютный минимум её на выпуклом множестве
строго выпукла, то абсолютный минимум её на выпуклом множестве  достигается в единственной точке (на середине отрезка, на концах которого
достигается в единственной точке (на середине отрезка, на концах которого 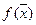 имеет равные значения, функция имеет меньшее значение).
имеет равные значения, функция имеет меньшее значение).
(--13--)
Дата: 2019-03-05, просмотров: 277.