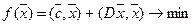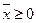
; ,

Здесь Х – полиэдр, то есть множество, задаваемое линейными условиями.

Здесь D – симметричная неотрицательно определённая матрица размером n*n,то есть:

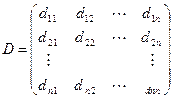, вектор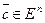

Задачи классов 6 и 7 в настоящее время наиболее хорошо изучены.

(--18--)

Задачи дискретной оптимизации (дискретного программирования)

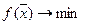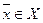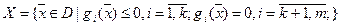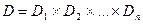, , где, , где  (декартово произведение), причём ,

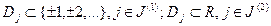Здесь 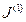 - некоторое подмножество множества {1,2,…,n},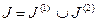

Если 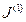={1,2,…,n}, то имеем задачу целочисленного программирования.

Задачи оптимального уравнения

Постановка этих задач сложнее постановки рассмотренных выше задач. Поэтому сначала рассмотрим содержательный пример:

Задача о строительстве дороги

Надо проложить дорогу на неровной местности между двумя пунктами. Затраты на строительство пропорциональны количеству завезённого и вывезенного с трассы грунта. Пусть Т –длина дороги, с(t) – известная высота местности в точке на расстоянии 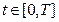 от начального пункта трассы. Определить функцию x(t), описывающую высоту дороги в каждой её точке 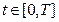, при которой затраты не её строительство минимальны. При этом наклон (уклон) дороги в любой точке трассы не должен быть больше b₁, т.е.  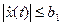для 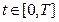. Скорость изменения наклона дороги не должна превышать константы b₂, то есть  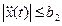для 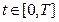. Уровень дороги в начальном и конечном пунктах определяется выражением x(0)=a, x(T)=b. Тогда математическая формулировка задачи такова:

минимизировать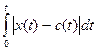

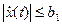
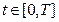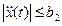
при условиях ; ; 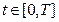x(0)=a, x(T)=b.

Параметром управления здесь является объем грунта, вывезенный или завезённый в точку трассы на расстоянии t от начального пункта, то есть величина, пропорциональная .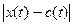

Перейдём теперь к общей постановке задачи оптимального управления:

Движение управляемого объекта описывается системой дифференциальных уравнений

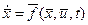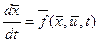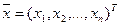, ( , где  (где 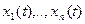) – n-мерный вектор координат состояния объекта, или фазовые координаты.

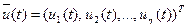 η-мерный вектор управления

t – время

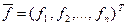 - n-мерный вектор функций.

(--19--)

Движение объекта подчинено начальным условиям ,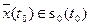

конечным условиям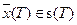

и ограничениям на фазовые координаты (фазовым ограничениям) ,  ( )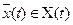

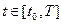кроме того, заданы ограничения на управление: ;  ( )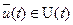

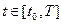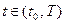Здесь  - отрезок времени, на котором происходит управление системой.

s₀(t₀), s(T), X(t), U(t) при каждом t – заданные множества из пространств соответствующих размерностей.

Итак, в этих задачах в качестве элементов, по которым ведётся минимизация, выступают функции. Эти задачи относятся к классу задач оптимизации в бесконечных функциональных пространствах.

Итак, общая модель такова:

,

,

;

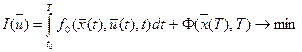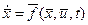
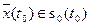
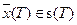
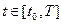
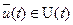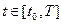
(Здесь функционал – это аналог функции цели в конечномерных задачах)

(--20--)

Тема 2. Линейное программирование. Введение