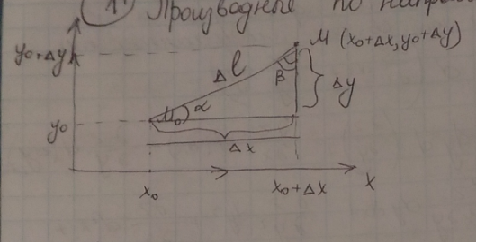
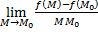Определение. Если существует конечный предел  по лучу 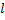, то говорят, что в точке  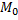существует производная функции  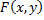по направлению  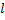и обозначается .

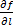Теорема. Если функция 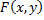 в точке  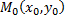имеет непрерывные частные производные, то в точке  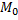существует производная по направлению, которая вычисляется по формуле

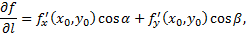
где 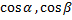 – направляющие косинусы направления .

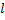Доказательство. Возьмём произвольные точк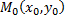и  и 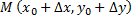.  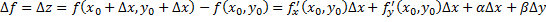( 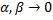, когда ).

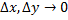Поделим обе части последнего неравенства на :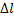

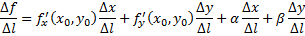
В последнем равенстве переходим к пределу

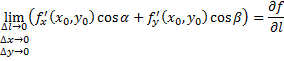
Определение. Градиентом скалярной функции 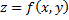 называется вектор, проекции которого на координатные оси совпадают с частными производными этой функции:

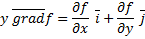
Возьмём единичный вектор 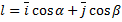 (составляющие по осям единичного вектора совпадают с направляющими косинусами этого направления).

Если эти равенства скалярно перемножить, получим: 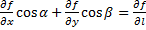. С другой стороны, если перемножить и пользоваться определением скалярного произведения,

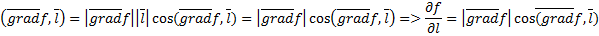
Следовательно, градиент 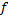 имеет направление быстрейшего увеличения функции по направлению  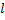и по величине равен производной функции по этому направлению.

                                                                        Билет №16 Экстремумы.    

Определение. Если в некоторой окрестности 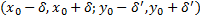 в точке  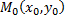выполняется неравенство  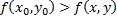( 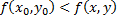), то говорят, что функция  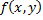имеет в точке  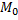максимум (минимум).

Теорема (необходимое условие экстремума). Если дифференцируемая функция 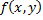 имеет экстремум в точке 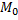, то обе частные производные  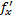и 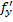 в этой точке равны нулю.

Доказательство. Допустим, 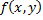 в точке  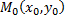имеет максимум, т.е.  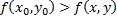(для некоторой окрестности 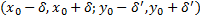). Рассмотрим только те точки, в которых 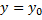. Тогда условие максимума будет записано в виде 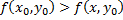. Это условие максимума для функции одной переменно, следовательно, по соответствующей теореме производная должна быть равна нулю: 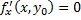. Но обычная производная, вычисленная 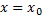, совпадает с частной производной по  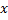функции 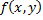, вычисленной в точке 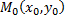, следовательно, 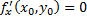. Аналогично рассматривая случай  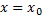и приводя аналогичные рассуждения, получим, что .

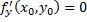Определение. Точки, где обе частные производные равны нулю, называются стационарными.

Данная теорема является необходимым условием нахождения экстремума, но не достаточным. Достаточное условие экстремума формулируется следующим образом.

Если в стационарной точке 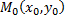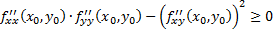, то при  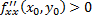( 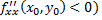в 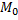 достигается минимум (максимум).

Билет №17 Ряды.

Определение. Рядом называется выражение, которое получится, если все члены последовательности 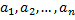 соединить формально знаком «плюс»: .

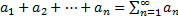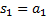 называется первой частичной суммой,  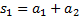– второй частичной суммой, …,  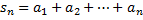– 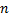-ой частичной суммой.

Определение:

Говорят, что бесконечный ряд сходится, если последовательность его частичных сумм стремится к некоторому числу

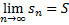 , в противном случае, говорят, что ряд расходится.

Некоторые ряды:

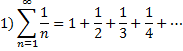
Гармонический ряд, всегда расходится.

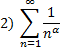
Обобщённый ряд Дирихле, при 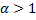 сходится, при  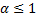– расходится.

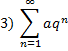
При 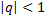 сходится, при  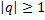– расходится.

Свойства сходящихся рядов.

1. (Необходимый признак сходимости ряда) Если ряд сходится, то его общий член стремится к нулю при .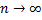

Доказательство. Пусть ряд 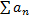 сходится, тогда 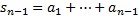, , 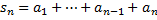следовательно, .

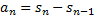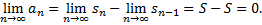
Замечание. Данный признак является необходимым, но не достаточным (например, гармонический ряд).

2. а) Если сходится бесконечный ряд, то сходится и любой его остаток.

б) Если сходится какой-либо остаток ряда, сходится и сам ряд.

3. Если ряд сходится, то есть остаток 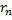 стремится к нулю.

Доказательство. Согласно определению остатка .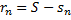

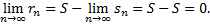
4. Пусть дан сходящийся ряд 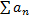, сумма которого равна 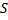. Если все члены этого ряда умножить на число 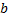, то получится новый сходящийся ряд, сумма которого равна .

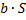Доказательство:

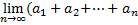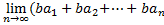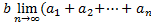S= )= )= )=bS=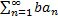

5. Пусть даны два сходящихся ряда 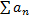, сумма которого равна  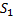и 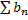, сумма которого равна 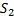. Если составить новый ряд 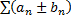, этот ряд также будет сходиться, а его сумма будет равна .

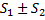6. Если в сходящемся ряде 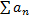 произвольно объединить члены ряда в группы, не меняя при этом порядка следования членов, сходимость ряда не нарушится, а сумма ряда не изменится.

Билет №18 Положительные ряды.(Необходимое и достаточное условие сходимости ряда)

Определение. Положительным рядом называется ряд, все члены которого неотрицательны.

Теорема (основная). Для того чтобы положительный ряд сходился, необходимо и достаточно, чтобы все его частичные суммы были ограничены сверху некоторым числом.

Доказательство. Необходимость. Пусть ряд 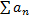 сходится, следовательно, существует предел 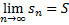. Так как ряд положительный,  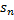стремится к  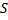возрастая, а значит,  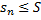(условие ограниченности).

(Последовательность частичных сумм ограничена сверху числом ).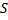

Достаточность. 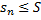. Тогда по теореме о монотонной переменной существует конечный предел последовательности частичных сумм, что 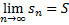. Из определения сходящегося ряда следует, что  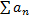сходится.