Теорема. Функция, непрерывная на отрезке, интегрируема на этом отрезке.

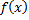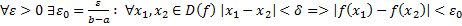Доказательство. Пусть функция  непрерывна на отрезке , тогда  (определение равномерно непрерывной функции). Если обозначить за  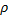максимум среди 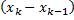, то из  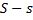получим:

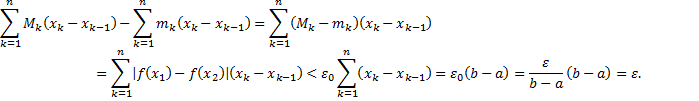
Доказали, что 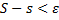, а значит,  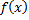интегрируема на отрезке  (см. предыдущую теорему).

Теорема. Функция, монотонная на отрезке, интегрируема на этом отрезке.

Доказательство. Рассмотрим случай, когда 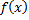 – возрастающая функция. Тогда нижняя и верхняя грани достигаются соответственно в левом и правом концах отрезков деления, т.е. 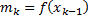,  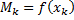(для убывающей функции – наоборот). Тогда для заданного 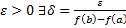. Получим:

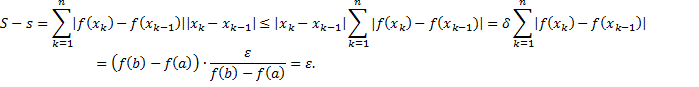
А значит, .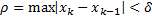

Билет №4 Основные свойства определённого интеграла.

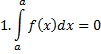
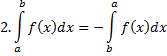
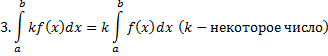
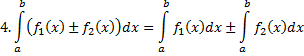
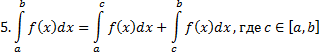
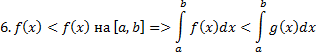
7. Если дана функция 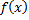, которая является непрерывной на отрезке , то справедливо следующее:

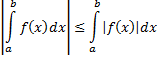
(Доказывается на основе одного из свойств абсолютной величины.)

Теорема (о среднем). Величина интеграла равна длине отрезка интегрирования, умноженной на число, заключённое между нижней и верхней гранями функций:

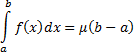
Доказательство. Из теории предыдущей лекции справедливо следующее:

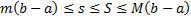
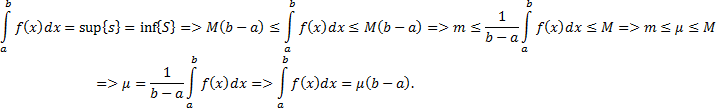
Замечание. Если 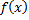 непрерывная на , то промежуточное значение она принимает в некоторой промежуточной точке, и тогда последняя формула принимает вид:

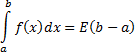
Билет №5 Интеграл с переменным верхним пределом.
Вычисление определённых интегралов.

Пусть 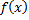 интегрируема на отрезке . Возьмём в качестве нижнего предела интегрирования произвольную точку 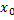 отрезка , а верхний предел оставим переменным, причём 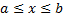. При этих условиях интеграл

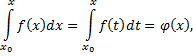
Где 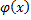 – функция, зависящая от 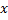, определённая на отрезке . Докажем, что 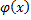 будет непрерывной. Если функция интегрируема, то  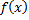будет ограничена функцией, откуда получим:

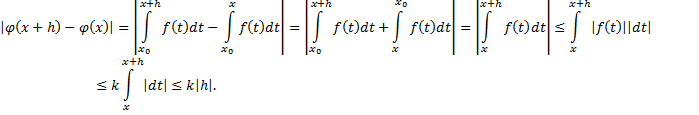
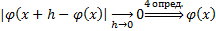 – непрерывная функция.

Теорема. Интеграл с переменным верхним пределом 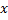 от функции, которая является непрерывной, есть функция дифференцируемая, причём производная от интеграла по верхнему пределу равна значению подынтегральной функции в точке .

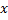Доказательство. Пусть 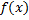 непрерывна на ,  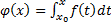в точке 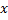. Для этого по определению производной найдём предел частного приращения функции и приращения аргумента:

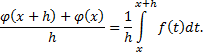
Если к интегралу применим теорему о среднем и перейдём к пределу при 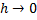, получим:

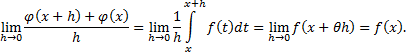
Вывод. Функция 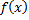, непрерывная в интервале, имеет в этом интервале первообразную: 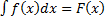. С другой стороны, интеграл с переменным верхним пределом также является первообразной для функции  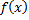на этом де отрезке: . Но для одной и той же функции две первообразные могут отличаться лишь на постоянное слагаемое, то есть

Если 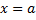, то

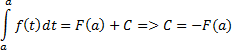
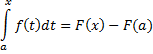
Если 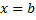, то

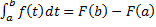 –формула Ньютона-Лейбница

Билет №6