Билет №1 Интеграл Римана (Определённый интеграл).
К понятию определённого интеграла приводят следующие задачи:
1. нахождение длины пройденного пути;
2. нахождение массы неоднородного стержня;
3. нахождение площади криволинейной трапеции и др.
Подробнее рассмотрим задачу о нахождении площади криволинейной трапеции:
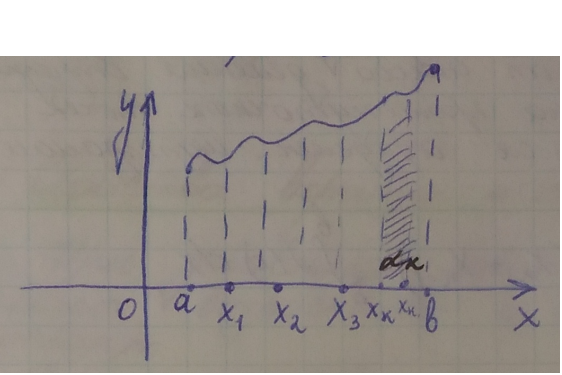
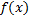 – неопределённая функция, находящаяся над осью
– неопределённая функция, находящаяся над осью  . Отрезок
. Отрезок  делим произвольным образом на
делим произвольным образом на  частей точками
частей точками 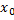 , …,
, …, 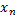 , так что
, так что 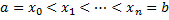 .
.
Из каждой точки 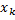 восстанавливаем перпендикуляры до пересечения с кривой
восстанавливаем перпендикуляры до пересечения с кривой  , тем самым деля криволинейную трапецию на
, тем самым деля криволинейную трапецию на 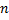 полосок. В каждой из частей
полосок. В каждой из частей  мы произвольным образом выбираем некоторую точку
мы произвольным образом выбираем некоторую точку 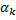 . Вычислим приблизительно площадь одной такой полоски:
. Вычислим приблизительно площадь одной такой полоски: 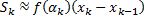 ,
, 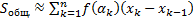 . Чем меньше деление отрезка
. Чем меньше деление отрезка  на приозвольные
на приозвольные 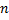 частей, тем точнее будет площадь данной фигуры при условии, что наибольшая из длин отрезков
частей, тем точнее будет площадь данной фигуры при условии, что наибольшая из длин отрезков 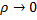 , то есть
, то есть
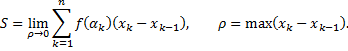
Определение. Величину 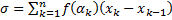 называют интегральной суммой для функции
называют интегральной суммой для функции 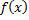 .
.
Определение. Площадью называют предел интегральной функции, который обладает следующим свойством: как бы ни было задано 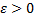 , можно найти такую
, можно найти такую  при условии, что
при условии, что  , что все интегральные суммы не зависят ни от способа деления отрезка
, что все интегральные суммы не зависят ни от способа деления отрезка  на части, ни от выбора точек
на части, ни от выбора точек 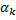 . Этот предел носит называние определённого интеграла и обозначается
. Этот предел носит называние определённого интеграла и обозначается

Где 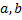 – нижний и верхний предел интегрирования.
– нижний и верхний предел интегрирования.
Билет № 2 Верхние и нижние суммы.
При стремящихся к нулю длин отрезков деления каждая из слагаемых интегральной суммы также стремится к нулю. При этом число слагаемых неограниченно возрастает. При этих условиях интегральная сумма может стремиться к какому-то пределу, но также может и не иметь этого предела. Для этого вводят понятия верхний и нижний суммы Дарбу. В силу ограниченности функции на данном отрезке она будет ограничена на каждом из отрезков деления отрезка  , следовательно, можно говорить о верхней и нижней гранях функции
, следовательно, можно говорить о верхней и нижней гранях функции 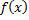 на этих отрезках, то есть
на этих отрезках, то есть

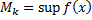

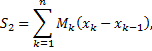
где 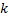 изменяется о т 1 до
изменяется о т 1 до 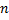 .
.
Объедененно эти суммы называют суммами Дарбу. ( 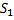 ≤0≤
≤0≤ 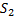 ) При геометрическом истолковании нижняя и верхняя суммы выражают площади двух ступенчатых фигур: одна из них содержится в криволинейной трапеции, а другая – содержит криволинейную трапецию.
) При геометрическом истолковании нижняя и верхняя суммы выражают площади двух ступенчатых фигур: одна из них содержится в криволинейной трапеции, а другая – содержит криволинейную трапецию.
Билет №6
Билет №7 Площадь.
Площади ступенчатых фигур, содержащиеся в данной фигуре и содержащие данную фигуру равны соответственно 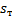 (нижняя сумма) и
(нижняя сумма) и  (верхняя сумма). С другой стороны, по предыдущей лекции для интеграла вида
(верхняя сумма). С другой стороны, по предыдущей лекции для интеграла вида 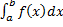 справедливо
справедливо  . Так как
. Так как 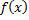 – непрерывная функция (а следовательно, интегрируемая), то можно поделить на части таким образом, чтобы
– непрерывная функция (а следовательно, интегрируемая), то можно поделить на части таким образом, чтобы 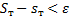 (условие квадрируемости для любого
(условие квадрируемости для любого 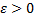 ). Поскольку два числа
). Поскольку два числа  и
и 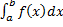 можно поместить в интервал сколь угодно малой длины таким образом, чтобы они совпадали, площадь плоской фигуры для кривой, заданной в декартовых координатах, определяется по формуле:
можно поместить в интервал сколь угодно малой длины таким образом, чтобы они совпадали, площадь плоской фигуры для кривой, заданной в декартовых координатах, определяется по формуле:

Замечание 1. Если кривая  и
и 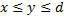 , то площадь находится как
, то площадь находится как 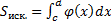 .
.
Замечание 2. Если требуется найти площадь плоской фигуры, находящейся под осью 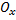 , интеграл берут с минусом.
, интеграл берут с минусом.
Замечание 3. Если требуется найти площадь плоской фигуры, ограниченной двумя кривыми, используют формулу
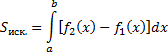
Если кривая задаётся в параметрической форме  , формула принимает вид
, формула принимает вид 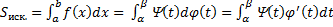
Если 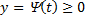 , то на отрезке
, то на отрезке  площадь криволинейной трапеции будем находить по вышеописанной формуле при условии, что
площадь криволинейной трапеции будем находить по вышеописанной формуле при условии, что 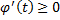 .
.
Если 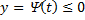 , то интеграл нужно взять по абсолютной величине:
, то интеграл нужно взять по абсолютной величине: 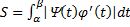 .
.
Во всех случаях, когда 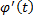 и
и  сохраняют свои знаки, нужно воспользоваться формулой
сохраняют свои знаки, нужно воспользоваться формулой 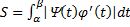 .
.
Пусть кривая задана в полярных координатах 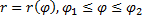 , а кривая
, а кривая  непрерывна на отрезке
непрерывна на отрезке  . Угол произвольным образом разбиваем на части, проводя радиус-векторы под некоторыми углами. В результате этого деления получим некоторые криволинейные секторы. Для определённости рассмотрим один криволинейный сектор, соответствующий изменению угла
. Угол произвольным образом разбиваем на части, проводя радиус-векторы под некоторыми углами. В результате этого деления получим некоторые криволинейные секторы. Для определённости рассмотрим один криволинейный сектор, соответствующий изменению угла  . Внутри проводим два круговых сектора: один внутри, другой – снаружи. Из школьного курса известно, для кругового сектора с наименьшим радиусом
. Внутри проводим два круговых сектора: один внутри, другой – снаружи. Из школьного курса известно, для кругового сектора с наименьшим радиусом 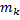 и наибольшим
и наибольшим  , один из которых содержит криволинейный сектор, а другой – содержится в нём, известны формулы их вычисления:
, один из которых содержит криволинейный сектор, а другой – содержится в нём, известны формулы их вычисления:
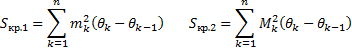
Так как 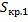 и
и 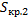 соответственно являются нижней и верхней суммой непрерывной функции
соответственно являются нижней и верхней суммой непрерывной функции 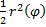 , при достаточно малой величине
, при достаточно малой величине 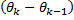 получим, что
получим, что  – площадь для вычисления фигуры, если кривая задаётся в полярных координатах.
– площадь для вычисления фигуры, если кривая задаётся в полярных координатах.
Билет №8 Длина дуги.
Кривая называется гладкой, если 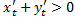
Пусть кривая 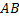 задана в параметрической форме
задана в параметрической форме 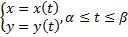 .
.
1)  Данную кривую произвольным образом с помощью параметра
Данную кривую произвольным образом с помощью параметра 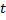 разбиваем на произвольные части:
разбиваем на произвольные части: 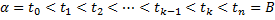 .
.
2) Эти точки соединяем отрезками. В результате получается некоторая ломаная. Чем меньше отрезки деления  , тем меньше длины
, тем меньше длины  (звенья ломаной).
(звенья ломаной).  (
( 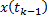 ,
,  ,
, 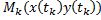
3) 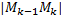
4) 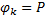 (длина дуги равна периметру ломаной)
(длина дуги равна периметру ломаной)
5) Длина ломаной:
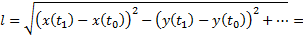
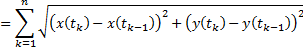
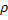 - расстояние между точками
- расстояние между точками
 max
max 
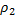 =max
=max 
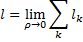
При 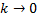 в отрезке
в отрезке  в силу непрерывности функций
в силу непрерывности функций 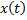 и
и  длина каждого звена также будет стремиться к нулю. В этом случае говорят, что кривая спрямляема, а
длина каждого звена также будет стремиться к нулю. В этом случае говорят, что кривая спрямляема, а 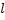 называют длиной дуги.
называют длиной дуги.
Теорема.
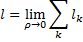
Гладкая кривая  , заданная в параметрической форме, является спрямляемой(имеет длину), и её длина вычисляется как
, заданная в параметрической форме, является спрямляемой(имеет длину), и её длина вычисляется как  – формула для вычисления длины дуги в параметрической форме.
– формула для вычисления длины дуги в параметрической форме.
1.
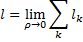
2.
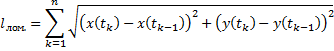
3. По формуле Лагранжа (о конечных приращениях)
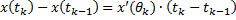 (
(  в формуле Лагранжа).
в формуле Лагранжа).
 .
.
4.
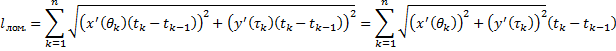
5.

где  – некоторая интегральная сумма для непрерывной функции
– некоторая интегральная сумма для непрерывной функции  . В силу непрерывности функций
. В силу непрерывности функций 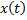 и
и  , рассмотрев абсолютную величину разности последних двух сумм, получим:
, рассмотрев абсолютную величину разности последних двух сумм, получим:
6. 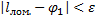
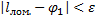
7. 
8. Если  задаётся в декартовых координатах
задаётся в декартовых координатах 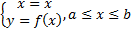 , подставляя в формулу (1), получаем:
, подставляя в формулу (1), получаем:

9. В полярных координатах:
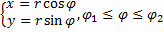

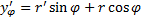
Подставляя в формулу (1), получаем:

Билет №9 Объём тела.
Определение. Ограниченная замкнутая область в пространстве называется телом.
Пусть 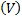 – некоторое тело,
– некоторое тело,  и
и 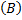 – содержащийся и содержащий многогранники данного тела соответственно:
– содержащийся и содержащий многогранники данного тела соответственно: 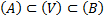 . За внутреннюю меру
. За внутреннюю меру  данного тела понимается верхняя грань объёмов многогранников, содержащихся в данном теле:
данного тела понимается верхняя грань объёмов многогранников, содержащихся в данном теле: 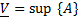 . За внешнюю меру
. За внешнюю меру 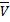 данного тела понимается нижняя грань объёмов многогранников, содержащих данное тело:
данного тела понимается нижняя грань объёмов многогранников, содержащих данное тело:  . Любая внутренняя мера не больше внешней. Если они равны между собой, говорят, что тело кубируемо, а
. Любая внутренняя мера не больше внешней. Если они равны между собой, говорят, что тело кубируемо, а 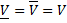 – его объём.
– его объём.
Критерий кубируемости. Для того чтобы тело было кубируемо, необходимо и достаточно, чтобы можно было указать два многогранника, один из которых содержится в теле, другой – содержит его, причём их объёмы сколь угодно мало отличаются друг от друга.
Из школьного курса известно, что объём тела может быть вычислен, когда известна площадь поперечных сечений тела:
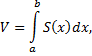
где  – площадь поперечного сечения.
– площадь поперечного сечения.
Разобьём отрезок  произвольным образом на
произвольным образом на 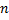 частей точками
частей точками  . Через эти точки деления проводим плоскости, которые разрежут наше тело на некоторые части
. Через эти точки деления проводим плоскости, которые разрежут наше тело на некоторые части 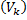 с толщиной
с толщиной  . На каждом слое два элементарных цилиндра с высотой
. На каждом слое два элементарных цилиндра с высотой  : один внутри, другой – содержит данный слой. Если площадь малого цилиндра обозначить черех
: один внутри, другой – содержит данный слой. Если площадь малого цилиндра обозначить черех  , а большого
, а большого 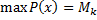 , то
, то 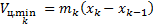 ,
,  .
.

Тогда разность этих объёмов 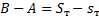 может быть сделана сколь угодно малой при достаточной малости отрезков
может быть сделана сколь угодно малой при достаточной малости отрезков  , т.к. представляет собой разность верхних и нижних сумм непрерывной, а следовательно, интегрируемой функции
, т.к. представляет собой разность верхних и нижних сумм непрерывной, а следовательно, интегрируемой функции  . Согласно предыдущим результатам получим, что
. Согласно предыдущим результатам получим, что  (формула для вычисления объёма тела по заданной площади поперечных сечений, принцип Кавальери). Кроме того, можно найти объём тела вращения для
(формула для вычисления объёма тела по заданной площади поперечных сечений, принцип Кавальери). Кроме того, можно найти объём тела вращения для  на некотором отрезке
на некотором отрезке  .
.
Так как поперечное сечение – круг
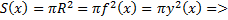
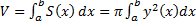 – формула для вычисления объёма тела вращения при вращении вокруг оси
– формула для вычисления объёма тела вращения при вращении вокруг оси 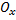 .
.
Замечание. При вращении вокруг оси  формула принимает вид
формула принимает вид
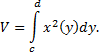
Билет №10
Определение. Последовательность точек 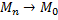 , если расстояние между точками
, если расстояние между точками  . В этом случае точка
. В этом случае точка 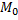 называется предельной точкой плоскости
называется предельной точкой плоскости  .
.
Теорема. Для того чтобы последовательность точек 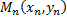 стремилась к точке
стремилась к точке 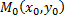 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  и
и 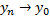 .
.
Доказательство. Необходимость. 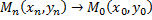 . Согласно определению
. Согласно определению  ,
,  .
.
Достаточность.  ,
, 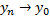 .
.
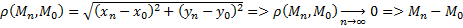 (по определению).
(по определению).
Теорема (Больцано – Вейерштрасса). Из всякой ограниченной плоскости точек на плоскости всегда можно выделить сходящуюся подпоследовательность, которая сходится к некоторой предельной точке.
Доказательство – см. семестр I.
Определение (по Гейне). Если для любой стремящейся к точке 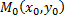 последовательности точек
последовательности точек 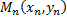 последовательности соответствующих значений функции
последовательности соответствующих значений функции 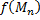 стремятся к одному и тому же пределу
стремятся к одному и тому же пределу  , то
, то  – предел функции
– предел функции 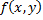 в точке
в точке 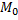 :
:
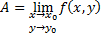
Определение (по Коши). Число  называется пределом функции
называется пределом функции 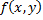 в некоторой точке
в некоторой точке 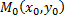 , если для сколь угодно малого
, если для сколь угодно малого 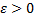 можно подобрать
можно подобрать  , такое, что для всех пар
, такое, что для всех пар  , которые удовлетворяют неравенствам
, которые удовлетворяют неравенствам  ,
, 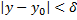 , из чего следует выполнение
, из чего следует выполнение 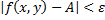 .
.
Билет №17 Ряды.
Определение. Рядом называется выражение, которое получится, если все члены последовательности  соединить формально знаком «плюс»:
соединить формально знаком «плюс»: 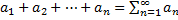 .
.
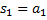 называется первой частичной суммой,
называется первой частичной суммой,  – второй частичной суммой, …,
– второй частичной суммой, …, 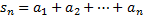 –
– 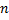 -ой частичной суммой.
-ой частичной суммой.
Определение:
Говорят, что бесконечный ряд сходится, если последовательность его частичных сумм стремится к некоторому числу
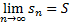 , в противном случае, говорят, что ряд расходится.
, в противном случае, говорят, что ряд расходится.
Некоторые ряды:

Гармонический ряд, всегда расходится.
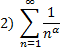
Обобщённый ряд Дирихле, при 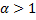 сходится, при
сходится, при 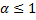 – расходится.
– расходится.
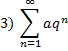
При 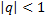 сходится, при
сходится, при 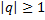 – расходится.
– расходится.
Свойства сходящихся рядов.
1. (Необходимый признак сходимости ряда) Если ряд сходится, то его общий член стремится к нулю при 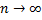 .
.
Доказательство. Пусть ряд 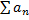 сходится, тогда
сходится, тогда 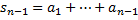 ,
, 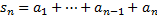 , следовательно,
, следовательно, 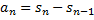 .
.
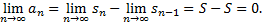
Замечание. Данный признак является необходимым, но не достаточным (например, гармонический ряд).
2. а) Если сходится бесконечный ряд, то сходится и любой его остаток.
б) Если сходится какой-либо остаток ряда, сходится и сам ряд.
3. Если ряд сходится, то есть остаток 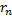 стремится к нулю.
стремится к нулю.
Доказательство. Согласно определению остатка  .
.

4. Пусть дан сходящийся ряд 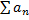 , сумма которого равна
, сумма которого равна 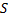 . Если все члены этого ряда умножить на число
. Если все члены этого ряда умножить на число 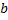 , то получится новый сходящийся ряд, сумма которого равна
, то получится новый сходящийся ряд, сумма которого равна 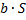 .
.
Доказательство:
S= 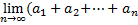 )=
)= 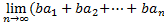 )=
)=  )=bS=
)=bS= 
5. Пусть даны два сходящихся ряда 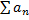 , сумма которого равна
, сумма которого равна 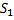 и
и 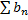 , сумма которого равна
, сумма которого равна 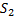 . Если составить новый ряд
. Если составить новый ряд 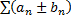 , этот ряд также будет сходиться, а его сумма будет равна
, этот ряд также будет сходиться, а его сумма будет равна 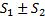 .
.
6. Если в сходящемся ряде 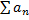 произвольно объединить члены ряда в группы, не меняя при этом порядка следования членов, сходимость ряда не нарушится, а сумма ряда не изменится.
произвольно объединить члены ряда в группы, не меняя при этом порядка следования членов, сходимость ряда не нарушится, а сумма ряда не изменится.
Билет №18 Положительные ряды.(Необходимое и достаточное условие сходимости ряда)
Определение. Положительным рядом называется ряд, все члены которого неотрицательны.
Теорема (основная). Для того чтобы положительный ряд сходился, необходимо и достаточно, чтобы все его частичные суммы были ограничены сверху некоторым числом.
Доказательство. Необходимость. Пусть ряд 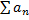 сходится, следовательно, существует предел
сходится, следовательно, существует предел 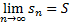 . Так как ряд положительный,
. Так как ряд положительный, 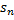 стремится к
стремится к 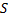 возрастая, а значит,
возрастая, а значит, 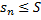 (условие ограниченности).
(условие ограниченности).
(Последовательность частичных сумм ограничена сверху числом 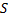 ).
).
Достаточность. 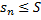 . Тогда по теореме о монотонной переменной существует конечный предел последовательности частичных сумм, что
. Тогда по теореме о монотонной переменной существует конечный предел последовательности частичных сумм, что 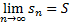 . Из определения сходящегося ряда следует, что
. Из определения сходящегося ряда следует, что 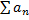 сходится.
сходится.
Признак Вейерштрасса.
Пусть дан функциональный ряд вида (1). Если существует положительный сходящийся ряд 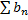 , такой что для всех
, такой что для всех 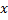 из промежутка
из промежутка  выполняется условие
выполняется условие 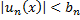 ,
, 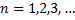 , то данный функциональный ряд равномерно и абсолютно сходится на отрезке
, то данный функциональный ряд равномерно и абсолютно сходится на отрезке  .
.
Доказательство:
Возьмем 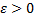 , существует такое N, что
, существует такое N, что


Для любого р→0
Из (2) следует 
Предел в левой части существует при р→0, тогда ряд будет абсолютно сходиться на промежутке  .
.
Тогда согласно свойствам абсолютной сходимости рядов, получим
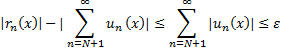
Доказывает, что для любого х принадлежащего промежутку  , ряд
, ряд 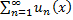 равномерно сходится на этом отрезке.
равномерно сходится на этом отрезке.
Билет №26 Свойство 1, о непрерывности суммы
Теорема 1. Если функции 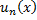 непрерывны на отрезке
непрерывны на отрезке  , и ряд
, и ряд 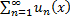 равномерно сходится, то
равномерно сходится, то  – непрерывная функция на этом отрезке.
– непрерывная функция на этом отрезке.
Доказательство. Возьмём 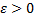 . Пользуясь равномерной сходимость ряда, для числа
. Пользуясь равномерной сходимость ряда, для числа 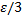 найдём такой номер
найдём такой номер 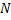 , что при
, что при 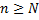 будет выполняться
будет выполняться  , где
, где 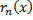 – остаток некоторого функционального ряда. По формуле
– остаток некоторого функционального ряда. По формуле 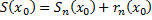 ,
,  (для любых
(для любых 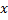 (
( 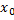 ) из промежутка
) из промежутка  ). Если вычесть из последнего предпоследнее равенство (или наоборот), получим:
). Если вычесть из последнего предпоследнее равенство (или наоборот), получим:
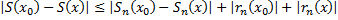 . Так как
. Так как  , получаем, что при любых
, получаем, что при любых 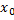 из промежутка
из промежутка 
 .
.

Последнее неравенство обозначает, что для любых 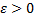 найдено такое
найдено такое  , что из
, что из  следует
следует 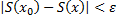 .
.
По определению непрерывной функции это означает, что  непрерывна в точке
непрерывна в точке 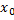 .
.
Билет №45
Нужно написать все разложения по формуле Тейлора + пример 
Билет №1 Интеграл Римана (Определённый интеграл).
К понятию определённого интеграла приводят следующие задачи:
1. нахождение длины пройденного пути;
2. нахождение массы неоднородного стержня;
3. нахождение площади криволинейной трапеции и др.
Подробнее рассмотрим задачу о нахождении площади криволинейной трапеции:

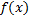 – неопределённая функция, находящаяся над осью
– неопределённая функция, находящаяся над осью 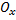 . Отрезок
. Отрезок  делим произвольным образом на
делим произвольным образом на 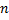 частей точками
частей точками 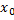 , …,
, …, 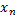 , так что
, так что 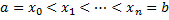 .
.
Из каждой точки 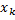 восстанавливаем перпендикуляры до пересечения с кривой
восстанавливаем перпендикуляры до пересечения с кривой  , тем самым деля криволинейную трапецию на
, тем самым деля криволинейную трапецию на 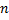 полосок. В каждой из частей
полосок. В каждой из частей  мы произвольным образом выбираем некоторую точку
мы произвольным образом выбираем некоторую точку 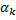 . Вычислим приблизительно площадь одной такой полоски:
. Вычислим приблизительно площадь одной такой полоски: 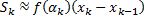 ,
, 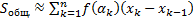 . Чем меньше деление отрезка
. Чем меньше деление отрезка  на приозвольные
на приозвольные 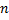 частей, тем точнее будет площадь данной фигуры при условии, что наибольшая из длин отрезков
частей, тем точнее будет площадь данной фигуры при условии, что наибольшая из длин отрезков 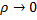 , то есть
, то есть
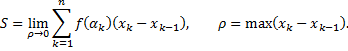
Определение. Величину 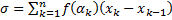 называют интегральной суммой для функции
называют интегральной суммой для функции 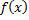 .
.
Определение. Площадью называют предел интегральной функции, который обладает следующим свойством: как бы ни было задано 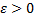 , можно найти такую
, можно найти такую  при условии, что
при условии, что  , что все интегральные суммы не зависят ни от способа деления отрезка
, что все интегральные суммы не зависят ни от способа деления отрезка  на части, ни от выбора точек
на части, ни от выбора точек 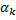 . Этот предел носит называние определённого интеграла и обозначается
. Этот предел носит называние определённого интеграла и обозначается

Где 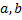 – нижний и верхний предел интегрирования.
– нижний и верхний предел интегрирования.
Дата: 2019-03-05, просмотров: 735.