Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Определить термический КПД и удельную работу цикла, теплоту, подведенную в процессе v=const и в процессе р=const, если известно:

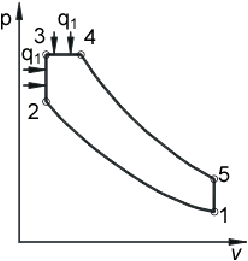
ДВС работает по циклу с комбинированным подводом теплоты.

расход топлива составляет m_T рабочего тела:

gm/kg

Начальные параметры:

начальная температура:

°C

начальное давление:

MPa

степень сжатия:

максимальное давление в цикле:

MPa

теплота сгорания топлива:

MJ/kg

Рабочее тело обладает свойствами воздуха, изобарную теплоемкость которого считать величиной постоянной и равной:

kJ/(kg K)

Решение

Определим изохорную теплоемкость воздуха, используя уравнение Майера и показатель адиабаты:

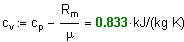
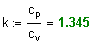
Определим о бщее колличество подведенной теплоты :

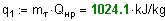
Рассчитаем у дельный объем в начальном состоянии :

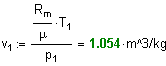
4. Определим т емпературу и давление воздуха в конце процесса адиабатного сжатия:

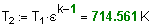
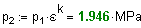
5. Рассчитаем Т₃ д ля изохорного процесса 2-3 :

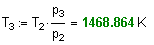
6. Найдем теплоту q_1.v :

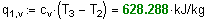
7. Рассчитаем теплоту q_1.p д ля изобарного процесса 3-4 :

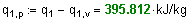
Определим температуру и удельный объем в точке 4:

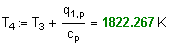
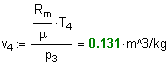
9. Найдем Т₅ д ля адиабатного процесса 4-5 :

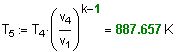
10. Рассчитаем теплоту процесса q₂:

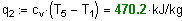
Определим удельную работу цикла:

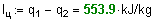
Находим КПД цикла:

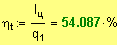
Третье начало термодинамики

Третье начало термодинамики - закон термодинамики, сформулированный В. Нерстом в 1906 году (тепловой закон Нернста), согласно которому энтропия S любой системы стремится к конечному для неё пределу, не зависящему от давления, плотности или фазы, при стремлении температуры (Т) к абсолютному нулю.

Третье начало термодинамики позволяет находить абсолютное значения энтропии, что нельзя сделать на основе первого и второго начал термодинамики. В классической термодинамике (первого и второго начал) энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S₀, что практически не мешает большинству термодинамических исследований, так как реально измеряется разность энтропий (S₀) в различных состояниях. Согласно третьему началу термодинамики при Т = 0 значение DS = 0.

М. Планк в 1911 году дал другую формулировку третьего начала термодинамики - как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю:

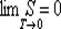(8)

Отсюда S₀ = 0. Это даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов.

Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S = klnW.

При абсолютном нуле температуры система находится в основном квантово-механическом состоянии, если оно невырождено, для которого W = 1 (состояние реализуется единственным микрораспределением. Следовательно, энтропия S при Т = 0 равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем может стать существенной при T → 0 дискретность квантовых уровней макроскопической системы, приводящая к явлениям квантового вырождения.

Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достигнуть ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться.

21. Теплопроводность. температурное поле

Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:

• теплопроводностью;
• конвекцией;
• излучением (радиацией).

Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.
Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом.
В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.
Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией). Этот процесс происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение э/м волн в пространстве, поглощение энергии излучения другим телом. Совместный теплообмен излучением и теплопроводностью называют радиационно-кондуктивным теплообменом.
Совокупность всех трех видов теплообмена называется сложным теплообменом.
Процессы теплообмена могут происходит в различных средах: чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т.д. В зависимости от этого теплообмен протекает по разному и описывается различными уравнениями.
Процесс переноса теплоты может сопровождаться переносом вещества (массообмен). Например испарение воды в воздух, движение жидкостей или газов в трубопроводах и.т.п. и.т.д. Тогда процесс теплообмена усложняется, так как теплота дополнительно переносится с массой движущегося вещества.

Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

 

 

t = f(x,y,z,τ) , (9.1)

где:t –температура тела;
x,y,z -координаты точки;
τ - время.
Такое температурное поле называется нестационарным ∂t/∂i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности
Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:

t = f(x,y,z) , ∂t/∂i = 0 (9.2)

Уравнение двухмерного температурного поля:
для нестационарного режима:

t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)

для стационарного режима:

t = f(x,y) , ∂t/∂z = 0; ∂t/∂i = 0 (9.4)

Уравнение одномерного температурного поля:
для нестационарного режима:

t = f(x,τ) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i ¹ 0 (9.5)

для стационарного режима:

t = f(x) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i = 0 (9.6)

Изотермической поверхностью называется поверхность тела с одинаковыми температурой.
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + ∆t.Градиентом температуры называют предел отношения изменения температуры∆tк расстоянию между изотермами по нормали ∆n, когда стремится к нулю:

gradt = |gradt| = lim[∆t/∆n]_∆n→0 = ∂t/∂n (9.7)

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормалиn:

 

 

gradt = ∂t/∂n n_o , (9.7^*)

где:n_o –единичный вектор.

Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком – Q, [Вт=Дж/с].
Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – q = Q / F, [Вт/м²]
Для твердого тела уравнение теплопроводности подчиняется закону Фурье:
||Тепловой поток, передаваемая теплопроводностью,||пропорциональна градиенту температуры и площади сечения,||перпендикулярного направлению теплового потока.

Q = -λ∙F∙ ∂t/∂n, (9.8)

или

q = -λ ∙ ∂t/∂n ∙n_o = -λ∙gradt , (9.9)

где: q –вектор плотности теплового потока;
λ – κоэффициент теплопроводности, [Вт/(м∙К)].
Численное значение вектора плотности теплового потока равна:

q = -λ∙ ∂t/∂n = -λ∙|gradt| , (9.10)

где:|gradt|- модуль вектора градиента температуры.
Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту, Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.
Дифференциальное уравнение теплопроводности для трехмерного нестационарного температурного поля имеет следующий вид:

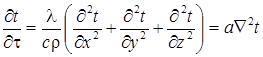, (9.11)

где: а = λ/(с·ρ) –коэффициент температуропроводности [м²/с], характеризует скорость изменения температуры.
Для стационарной задачи, дифференциальное уравнение имеет вид:

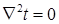. (9.12)

22.

Конвективным теплообменом, или теплоотдачей, называется процесс переноса тепла между поверхностью твердого тела и жидкой средой. При этом перенос тепла осуществляется одновременным действием теплопроводности и конвекции.

Явление теплопроводности в жидкостях и газах, так же как и в твердых телах, вполне определяется коэффициентом теплопровод­ности и температурным градиентом (см. разд. 2). Иначе обстоит дело с явлением конвекции — вторым элементарным видом распростра­нения тепла. Здесь процесс переноса тепла неразрывно связан с пе­реносом самой среды. Поэтому конвекция возможна лишь в жидко­стях и газах, частицы которых легко могут перемещаться.

По природе возникновения различают два вида движения — свободное и вынужденное. Свободным называется движение, происходящее вследствие разности плотностей нагретых и холодных частиц жидкости в поле тяжести. Возникновение и интенсивность свободного движения определяются тепловыми условиями процес­са и зависят от рода жидкости, разности температур, напряженности гравитационного поля и объема пространства, в котором проте­кает процесс. Свободное движение называется также естественной конвекцией. Вынужденным называется движение, возникающее под действием посторонних возбудителей, например насоса, вентилятора и пр. В общем случае наряду с вынужденным движением одно­временно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдель­ных точках жидкости и чем меньше скорость вынужденного дви­жения.

Интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи 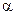, который определяется по формуле Ньютона

	(4.1)

 

Q = (t_c - t_ж).

Согласно этому закону количество переданного тепла Q про­порционально поверхности теплообмена F и разности температур стенки и жидкости (t_c—t_ж).

Коэффициент теплоотдачи можно определить как количество тепла, переданное в единицу времени через единицу поверхности при разности температур между поверхностью и жидкостью в один градус:

(4.2)

В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и различают поэтому средний по поверхности коэффициент теплоотдачи и локальный или местный коэффициент теплоотдачи, соответ­ствующий единичному элементу поверхности.

Процессы теплоотдачи нераз­рывно связаны с условиями движе­ния жидкости. Как известно из курса гидравлики, име­ются два основных режима тече­ния: ламинарный и турбулентный. При ламинарном режиме течение имеет спокойный, струйчатый ха­рактер. При турбулентном — дви­жение неупорядоченное, вихревое. Изменение режима дви­жения происходит при некоторой «критической» скорости, которая в каждом конкретном случае различна.

 

 

В результате специальных исследований О. Рейнольдс в 1883 г. установил, что в общем случае режим течения жидкости определя­ется не только одной скоростью, а особым безразмерным комплек­сом, состоящим из скорости движения жидкости w, коэффици­ента кинематической вязкости жидкости v и характерного размера l канала или обтекаемого тела. Теперь такой комплекс называется критерием или числом Рейнольдса и обозначается символом Re = wl/v.

Как известно из гидродинамики, критерий Рейнольдса, называемый иначе критерием кинематического подобия, характеризует соотношение между инерционными силами и силами трения и является основной характеристикой, определяющей режим течения жидкости. Переход ламинарного режима в турбулентный происходит при критическом значении этого критерия Re_кр. Например, при дви­жении жидкости в трубах Re_кр=w_кpd/v=2·10³.

При турбулентном движении весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и исчеза­ют. В точности механизм вихреобразования еще не установлен. Одной из причин их возникновения является потеря устойчивости ламинарного течения, сопровождающаяся образованием завихре­ний, которые затем диффундируют в ядро и, развиваясь, заполня­ют весь поток. Одновременно с этим вследствие вязкости жидкости эти вихри постепенно затухают и исчезают. Благодаря непрерыв­ному образованию вихрей и их диффузии происходит сильное перемешивание жидкости, называемое турбулентным смешением. Чем больше вихрей, тем интенсивнее перемешивание жидкости и тем больше турбулентность потока. Различают естественную и ис­кусственную турбулентность. Первая устанавливается естественно. Для случая стабилизированного движения внутри гладкой трубы турбулентность вполне определяется значением критерия Re. Вторая вызывается искусственным путем вследствие наличия в потоке каких-либо преград, турбулизирующих решеток и других возмущающих источников. Однако при любом виде турбулентности в тонком слое у поверхности из-за наличия вязкого трения течение жидкости затормаживается и скорость падает до нуля. Этот слой принято называть пограничным или вязким подслоем.

 

 

Теория пограничного слоя была разработана Л. Прандтлем в начале прошлого столетия (1904 г.)

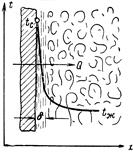
Рис. 4-1. Характер изме­нения температуры в по­граничном слое при на­гревании жидкости.

Для процессов теплоотдачи режим движения рабочей жидкости имеет очень большое значение, так как им определяется механизм переноса тепла. При ламинар­ном режиме перенос тепла в направление нормали к стенке в основном осуществля­ется путем теплопроводности. При турбу­лентном режиме такой способ переноса тепла сохраняется лишь в вязком подслое, а внутри турбулентного ядра перенос осуще­ствляется путем интенсивного перемешивания частиц жидкости. В этих условиях для газов и обычных жидкостей интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим. В этом легко убедиться, если проследить за изменением температуры жидкости в направлении нормали к стенке (рис. 4.1). Как видно, наибольшее изменение температуры происходит в пределах тонкого слоя у поверхности, через который тепло передается путем теплопроводности. Следовательно, как для лами­нарного, так и для турбулентного режима течения вблизи самой поверхности применим закон Фурье:

(4.3)

q = -λ grad t,

где grad t — градиент температуры в слоях жидкости, прилегаю­щих к поверхности твердого тела, °С/м.

Процесс теплоотдачи является сложным процессом, а коэффи­циент теплоотдачи является сложной функцией различных величин, характеризующих этот процесс. В общем случае коэффициент теплоотдачи является функцией формы Ф, размеров l₁, l₂, ..., температуры поверхности нагрева t_с, скорости жидкости w, ее температуры t_ж, физических свойств жидкости — коэффициента теплопроводно­сти λ, теплоемкости с_р, плотности ρ, вязкости μ и других факторов:

	(4.4)

 

α=f(w, t_c, t_ж, λ, с_р, ρ, μ, а, Ф, l_{1 ,} l₂...).

В качестве теплоносителей в настоящее время применяются са­мые разнообразные вещества — воздух, газы, вода, масла, бензол, нефть, бензин, спирты, расплавленные металлы и различные специ­альные смеси. В зависимости от рода и физических свойств этих ве­ществ теплоотдача протекает различно и своеобразно. Для каждо­го теплоносителя физические свойства имеют определенные значения и, как правило, являются функцией температуры, а некоторые из них и давления.

Коэффициент теплопроводности λ характеризует способность вещества проводить тепло; его значение определяет количество теп­ла, которое проходит в единицу времени через 1 м² сечения при из­менении температуры в один градус на 1 м пути теплового потока (см. разд. 2).

Удельная теплоемкость с определяет количество тепла, необходимое для нагревания 1 кг вещества на один градус. При постоянном давлении теплоемкость обозначается c_р (изобарная теплоемкость), а при постоянном объеме c_v (изохорная теплоемкость).

Плотность вещества ρ = m/V представляет собой массу веще­ства в единице объема.

Коэффициент температуропроводности а=λ/сρ характеризует скорость изменения температуры в теле (см. разд. 2).

Вязкость. Все реальные жидкости обладают вязкостью; между частицами или слоями, движущимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. Согласно закону вязкого трения Ньютона эта сила, от­несенная к единице поверхности, пропорциональна изменению ско­рости в направлении нормали к этой поверхности:

(4.5)

.

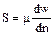Величина μ называется коэффициентом вязкости или коэффициентом динамической вязкости.

При dw/dn=1 S = μ, следовательно, коэффициент вязкости вы­ражает собой силу трения, приходящуюся на единицу поверхности соприкосновения двух жидких слоев, «скользящих» друг по другу при условии, что на единицу длины нормали к поверхности ско­рость движения изменяется на единицу.

В уравнения гидродинамики и теплопередачи часто входит от­ношение коэффициента вязкости к плотности, называемое коэффи­циентом кинематической вязкости:

	(4.6)

 

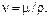
Температурный коэффициент объемного расширения 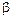харак­теризует относительное изменение объема при изменении темпе­ратуры на один градус:

(4.7)

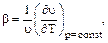
где υ — удельный объем, м³/кг.

Для газов температурный коэффициент объемного расширения определяется по формуле

	(4.8)

 

β=1/T.

Механизм и интенсивность переноса теплоты зависят от характера движения жидкости в пограничном слое. Если движение внутри теп­лового пограничного слоя ламинарное, то теплота в направлении, пер­пендикулярном к стенке, переносится теплопроводностью. Однако у внешней границы слоя, где температура по нормали к стенке меняется незначительно, преобладает перенос теплоты конвекцией вдоль стенки.

При турбулентном течении в тепловом пограничном слое пере­нос теплоты в направлении к стенке в основном обусловлен турбулентным перемешиванием жидкости. Интенсивность такого переноса теп­лоты существенно выше интенсивности переноса теплоты теплопровод­ностью. Однако непосредственно у стенки, в ламинарном подслое, пе­ренос теплоты к стенке осуществляется обычной теплопроводностью.

Изменение физических свойств жидкости в пограничном слое зави­сит от температуры, в связи с чем интенсивность теплообмена между жидкостью и стенкой оказывается различной в условиях нагревания и охлаждения жидкости. Так, например, для капельных жидкостей интенсивность теплообмена при нагревании будет большей, чем при охлаждении, вследствие уменьшения пограничного слоя. Следова­тельно, теплоотдача зависит от направления теплового потока.

Очень большое значение для теплообмена имеют форма и размер поверхностей; в зависимости от них может резко меняться характер движения жидкости и толщина пограничного слоя.