В процессе выбора финансовых инструментов инвестирования каждый инвестор ставит перед собой две основные задачи – максимизировать доход и минимизировать риск обращения. В связи с противоречивым характером этих задач процесс обоснования носит оптимизационный характер. Средством такой оптимизации выступают разнообразные модели оценки стоимости финансовых инструментов инвестирования, в основе которых лежит выявление оптимальной шкалы соотношений уровней доходности и риска, удовлетворяющих любого инвестора.
Современная теория выделяет следующие основные модели оценки стоимости финансовых инструментов инвестирования:
1) Модель оценки стоимости финансовых активов У. Шарпа;
2) Модель оценки стоимости финансовых активов исходя из нулевой «беты» Ф. Блэка;
3) Модель теории арбитражного ценообразования С. Росса;
4) Многофакторная модель оценки стоимости финансовых активов Р. Мертона.
1.1. Модель оценки стоимости финансовых активов У. Шарпа исходит из того, что каждая ценная бумага является частью общей совокупности ценных бумаг, обращающихся на фондовом рынке, то есть частью так называемого «рыночного портфеля».
При равновесном состоянии спроса и предложения на фондовом рынке стоимость рыночного портфеля отражает среднее соотношение уровня его доходности и риска. Модель оценки стоимости финансовых активов У. Шарпа задается коэффициентом «бета», который показывает предельный вклад доходности данной ценной бумаги в дисперсию доходности рыночного портфеля в целом.
При наличии статистических данных о доходности конкретного (i-го) вида ценных бумаг коэффициент b можно определить из выражения:
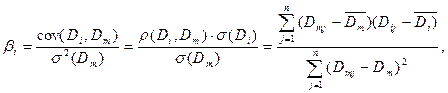
(1)
где Di, Dm – соответственно доходность i-го вида акций и среднерыночная доходность акций;
cov (Di, Dm) – ковариация доходности i-го вида акций и среднерыночной доходности акций;
r (Di, Dm) – коэффициент корреляции доходности i-го вида акций и среднерыночной доходности акций;
s2 (Dm)– дисперсия среднерыночной доходности акций;
s (Di), s (Dm) – соответственно среднеквадратическое отклонение i-го вида акций и среднерыночной доходности акций;
П– количество интервалов времени в рассматриваемом периоде (объем выборки);
Dij, Dmj – соответственно доходность i-го вида акций и среднерыночная доходность акций за j-й интервал времени;
Di, Dm – соответственно средняя доходность i-го вида акций и средняя среднерыночная доходность акций за весь рассматриваемый период.
С учетом этого, модель оценки стоимости финансовых активов У. Шарпа представляет собой следующую формулу:
| Дфа = Дбр +b (Дрп – Дбр), | (2) |
где Дфа – уровень ожидаемой доходности рассматриваемого финансового актива;
Дбр – уровень доходности безрискового финансового инструмента;
b – коэффициент «бета»;
Дрп – уровень ожидаемой доходности рыночного портфеля в целом.
Уровень дополнительного дохода инвестора за принимаемый на себя риск в процессе приобретения конкретной ценной бумаги характеризуется термином «премия за риск и определяется по следующей формуле:
| ПР = bфа (Дрп – Дбр), | (3) |
где bфа – коэффициент «бета» рассматриваемого финансового актива.
Таким образом, в основе модели оценки стоимости финансовых активов У. Шарпа лежит однофакторная модель зависимости этой стоимости от поведения рынка в целом (от динамики ожидаемого уровня доходности совокупного рыночного портфеля).
1.2. Модель оценки стоимости финансовых активов исходя из нулевой «беты» Ф. Блэка является модификацией модели У. Шарпа. Соответственно своим теоретическим посылкам, Ф Блэк внес изменения в классическую модель, представив ее в следующем виде:
| Дфа = Дфа0 + bфа (Дрп – Дфа0 ), | (4) |
где Дфа – уровень ожидаемой доходности рассматриваемого финансового актива;
Дфа0 – уровень доходности финансового инструмента с «бета» равной нулю;
bфа – коэффициент «бета» рассматриваемого финансового актива;
Дрп – уровень ожидаемой доходности рыночного портфеля в целом.
1.3. Многофакторная модель оценки стоимости финансовых активов Р. Мертона дополняет классическую модель. Р. Мертон считает, что оценка стоимости финансового актива должна учитывать не только систематический риск, но и уровень несистематического риска. Каждый из ожидаемых видов риска рассматривается как самостоятельный фактор формирования стоимости рассматриваемого финансового актива.
| Дфа = Дбр + bфа (Дрп – Дбр) + [bфа1 (Дрп1 – Дбр) + … + bфаn (Дрпn – Дбр)], | (5) |
где Дфа – уровень ожидаемой доходности рассматриваемого финансового актива;
bфа – коэффициент «бета» рассматриваемого финансового актива;
Дрп – уровень ожидаемой доходности рыночного портфеля в целом;
Дбр – уровень доходности безрискового финансового инструмента;
bфа1 ….bфаn – коэффициент «бета», измеряющий чувствительность актива к изменению доходности рыночного портфеля под влиянием несистематических рисков (факторов);
Дрп1 … Дрпn –уровень ожидаемой доходности рыночного портфеля в целом, компенсирующий несистематические риски.
1.4. Модель теории арбитражного ценообразования С. Росса предложена как альтернатива классической модели. Теория арбитражного ценообразования утверждает, что ожидаемая доходность отдельной ценной бумаги зависит от множества разнообразных факторов, а не одного интегрированного рыночного фактора, отражаемого классической моделью. В качестве таких факторов он рассматривает все виды систематических рисков раздельно, предлагая компенсировать каждый в процессе оценки стоимости финансового актива.
Дфа = Дбр + b1 (Дрп1 – Дбр) + b2 (Дрп2 – Дбр) + … + bn (Дрпn – Дбр)], (6)
где Дфа – уровень ожидаемой доходности рассматриваемого финансового актива;
Дрп – уровень ожидаемой доходности рыночного портфеля в целом;
Дбр – уровень доходности безрискового финансового инструмента;
b1 ….bn – коэффициент «бета», измеряющий чувствительность актива к фактору;
Дрп1 … Дрпn –уровень ожидаемой доходности рыночного портфеля в целом, компенсирующий несистематические риски;
n – общее количество рассматриваемых факторов, систематически влияющих на уровень доходности отдельных финансовых активов и рыночного портфеля в целом.
Таким образом, несмотря на определенную взаимную противоречивость, все рассмотренные модели оценки стоимости финансовых активов позволяют в совокупности сформировать систему практических принципов и методов осуществления оценки уровня эффективности и риска отдельных видов финансовых инструментов инвестирования.
1.5. Рассмотрим основные модели, используемые при формировании текущей рыночной цены акции:
1. Модель оценки стоимости простой акции при ее использовании в течение неопределенного продолжительного периода времени:
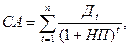
| (7) |
где СА – реальная стоимость акции, используемой неопределенное число лет;
Дt – сумма дивидендов, предполагаемая к получению в каждом периоде;
НП – ожидаемая доходность по акциям;
t – число периодов, включенных в расчет.
Экономическое содержание данной модели заключается в том, что текущая рыночная стоимость акции представляет собой сумму дивидендов по отдельным периодам, приведенную к настоящей стоимости по дисконтной ставке, равной норме текущей доходности по ней.
2. Модель оценки текущей рыночной стоимости акций при их использовании в течение заранее определенного срока:
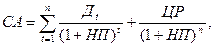
| (8) |
где ЦР – прогнозируемая рыночная цена реализации акции в конце периода ее использования.
3. Модель оценки текущей рыночной стоимости акций с постоянными дивидендами:
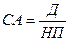 , ,
| (9) |
где Д – годовая сумма постоянного дивиденда.
4. Модель оценки текущей рыночной стоимости акций с постоянно возрастающими дивидендами (модель Гордона):
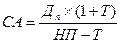 , ,
| (10) |
где Дп – сумма последнего уплаченного дивиденда;
Т – темп прироста дивидендов, выраженный десятичной дробью.
5. Модель оценки стоимости акций с колеблющимся уровнем дивидендов по отдельным периодам:
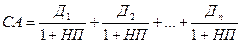 , ,
| (11) |
где Д1 … Дn – сумма дивидендов, прогнозируемых к получению в каждом периоде.
Указанные модели оценки реальной рыночной стоимости акций используются для их отбора и включения в инвестиционный портфель.
1.6. Рассмотрим основные модели, используемые при формировании текущей рыночной цены облигации:
1. Базисная модель оценки стоимости облигации или облигации с периодической выплатой процентов:
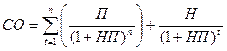 , ,
| (12) |
где СО – стоимость облигации;
П – сумма процента, выплачиваемая в каждом периоде (представляющая собой произведение ее номинала на объявленную ставку процента);
Н – номинал облигации, подлежащий погашению в конце срока ее обращения.
2. Модель оценки стоимости облигации с выплатой всей суммы процентов при ее погашении:
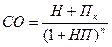 , ,
| (13) |
где Пк – сумма процента по облигации, подлежащая выплате в конце срока ее обращения.
3. Модель оценки стоимости облигации, реализуемой с дисконтом без выплаты процентов:
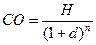 , ,
| (14) |
где d – дисконт.
Трансформируя указанные модели (меняя искомый расчетный показатель) можно рассчитать ожидаемую доходность. Доходность акций и облигаций вычисляется в следующем порядке.
Дивидендная норма доходности акции:
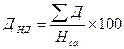 , ,
| (15) |
где SД – сумма дивидендов по акции;
Нса – номинальная стоимость акции.
Текущая норма доходности акции:
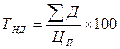 , ,
| (16) |
где ЦП – цена приобретения акции.
Для оценки текущего уровня доходности облигации используется коэффициент ее текущей доходности:
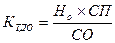 , ,
| (17) |
где Но – номинал облигации;
СП – объявленная ставка процента (купонная ставка);
СО – реальная текущая стоимость облигации (или текущая ее цена).
Дата: 2019-02-19, просмотров: 391.