Существуют универсальные методы обнаружения и устранения систематических погрешностей. Рассмотрим некоторые методы из них.
Метод противопоставления – измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.
Например, измерить сопротивление с помощью одинарного моста методом противопоставления.
Сначала измеряемое сопротивление Rx уравновешивают известным сопротивлением R1, включённым в плечо сравнения моста. При этом: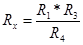 
, где R3, R4 – сопротивление плеч моста. Затем резисторы Rx и R1 меняют местами и вновь уравновешивают мост, регулируя сопротивление резистора R1. В этом случае: 
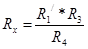. Тогда измеряемое сопротивление находится по формуле: 
.
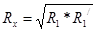Метод компенсации погрешности по знаку предусматривает измерение с двумя измерениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками. Результат измерения получим как полусумму двух результатов измерений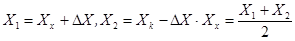 
.
Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие методы.
Метод симметрических наблюдений. Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y=kx+y0, где x, y – входная и выходная величины преобразователя; k – коэффициент, погрешность которого изменяется во времени по линейному закону; y0 – постоянная. Для устранения систематической погрешности трижды измеряется выходная величина y через равные промежутки времени Δt. При первом и третьем измерениях на вход преобразователя подаётся сигнал x0 от образцовой меры. В результате измерений получается система уравнений:
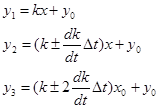
Её решение позволяет получить значение x, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k.
Метод последовательных разностей – применяется для обнаружения изменяющихся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдения можно оценить двумя способами: обычным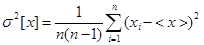 
.
И вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей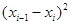 
: 
.
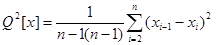Если в процессе измерений происходило смещение центра группирование результатов наблюдений, т.е. имела место переменная систематическая погрешность, то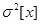 
даёт преувеличенную оценку дисперсии результатов наблюдений. Отношение 
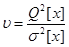является критерием для обнаружения систематических смещений центра группированием результатов наблюдений. Если полученное значение критерия меньше vq при заданных q и n(см. таблицу 2), то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений. Где n – число измерений, q – доверительная вероятность.
Таблица 2. Значения критерия Аббе.
| n | Vq при q равном | n | Vq при q равном | ||||
| 0.001 | 0.01 | 0.05 | 0.001 | 0.01 | 0.05 | ||
| 4 | 0.295 | 0.313 | 0.390 | 13 | 0.295 | 0.431 | 0.578 |
| 5 | 0.208 | 0.269 | 0.410 | 14 | 0.311 | 0.447 | 0.591 |
| 6 | 0.182 | 0.281 | 0.445 | 15 | 0.327 | 0.461 | 0.603 |
| 7 | 0.185 | 0.307 | 0.468 | 16 | 0.341 | 0.474 | 0.614 |
| 8 | 0.202 | 0.331 | 0.491 | 17 | 0.355 | 0.487 | 0.624 |
| 9 | 0.221 | 0.354 | 0.512 | 18 | 0.368 | 0.499 | 0.633 |
| 10 | 0.241 | 0.376 | 0.531 | 19 | 0.381 | 0.510 | 0.642 |
| 11 | 0.260 | 0.396 | 0.548 | 20 | 0.393 | 0.520 | 0.650 |
| 12 | 0.278 | 0.414 | 0.564 | ||||
Рассмотрим пример применения метода последовательных разностей для обнаружения изменяющейся во времени систематической погрешности. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 13.4 | 13.3 | 14.5 | 13.8 | 14.5 | 14.6 | 14.1 | 14.3 | 14.0 | 14.3 |
1. Вычислим среднее арифметическое измеряемой величины:
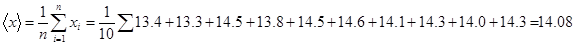
2. Вычислим дисперсию:
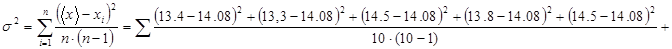
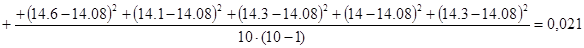
3. Вычислим сумму квадратов последовательных разностей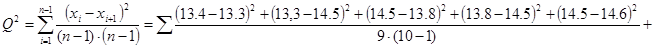 
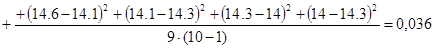
4. Вычислим отношение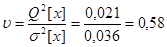 
.
5. Определим табличное значение критерия Аббе для n=10 и q=0.05 Vq=0.531. Так как отношение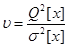 
меньше табличного значения, значит систематическая погрешность отсутствует.
Варианты задач для самостоятельной работы:
Вариант 1. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 10 | 10,7 | 9,7 | 9,7 | 10,5 | 10 | 9,6 | 10,2 | 10,5 | 10,2 |
Вариант 2. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,999.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 4,9 | 5 | 5,3 | 4,8 | 5,1 | 5,2 | 4,7 | 5,6 | 5,1 | 5 |
Вариант 3. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,999.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 20 | 20,7 | 19,7 | 19,7 | 20,5 | 20,4 | 19,7 | 20,2 | 20,4 | 20,3 |
Вариант 4. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 14,5 | 15,1 | 15,5 | 14,9 | 15,2 | 15,2 | 14,7 | 15,6 | 15,1 | 15,1 |
Вариант 5. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 10,1 | 10,2 | 9,5 | 9,8 | 10,6 | 10,1 | 9,6 | 10,1 | 10,6 | 10,3 |
Вариант 6. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 14,9 | 15 | 15,3 | 14,8 | 15,1 | 15,2 | 14,7 | 15,6 | 15,1 | 15 |
Вариант 7. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 2 | 2,7 | 1,7 | 1,7 | 2,6 | 2,5 | 1,6 | 2,1 | 2,5 | 2,3 |
Вариант 8. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 10,5 | 10,1 | 10,5 | 10,9 | 10,2 | 10,2 | 10,7 | 10,6 | 10,1 | 10,1 |
Вариант 9. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 10,5 | 10,1 | 10,5 | 10,9 | 10,2 | 10,2 | 10,7 | 10,6 | 10,1 | 10,1 |
Вариант 10. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,999.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 24,8 | 25 | 25,4 | 24,8 | 25,1 | 25,2 | 24,7 | 25,6 | 25,1 | 25,0 |
Вариант 11. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 12 | 12,7 | 11,7 | 11,7 | 12,6 | 12,5 | 11,6 | 12,1 | 12,5 | 12,3 |
Вариант 12. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 11,5 | 12,1 | 11,5 | 11,9 | 12,2 | 12,2 | 11,7 | 11,6 | 12,1 | 12,1 |
Вариант 13. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 11,5 | 12,1 | 11,5 | 11,9 | 12,2 | 12,2 | 11,7 | 11,6 | 12,1 | 12,1 |
Вариант 14. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 11,5 | 12,1 | 11,5 | 11,9 | 12,2 | 12,2 | 11,7 | 11,6 | 12,1 | 12,1 |
Вариант 15. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,999.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 2 | 2,6 | 1,6 | 1,7 | 2,6 | 2,5 | 1,6 | 2,1 | 2,5 | 2,4 |
Вариант 16. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 2 | 2,6 | 1,6 | 1,7 | 2,6 | 2,5 | 1,6 | 2,1 | 2,5 | 2,4 |
Вариант 17. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 5,3 | 5,2 | 4,5 | 4,8 | 4,6 | 5,2 | 4,6 | 5,4 | 5,6 | 5,3 |
Вариант 18. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 14,7 | 15 | 15,2 | 14,9 | 15,1 | 15,4 | 14,7 | 15,5 | 15,3 | 15,2 |
Вариант 19. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,95.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 14,7 | 15 | 15,2 | 14,9 | 15,1 | 15,4 | 14,7 | 15,5 | 15,3 | 15,2 |
Вариант 20. Используя метод последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений. Доверительная вероятность α=0,99.
| Число измерений | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Значения измеряемой величины, мкА | 14,7 | 15 | 15,2 | 14,9 | 15,1 | 15,4 | 14,7 | 15,5 | 15,3 | 15,2 |
Дата: 2019-02-19, просмотров: 435.
