Для начала дадим определение погрешности измерений.

Погрешность измерений – разность между полученным при измерении X и истинным Q значениями измеряемой величины.

В качестве обзора погрешностей измерений приведем классификацию измерений.

По способу выражения погрешности делятся:

Абсолютная погрешность – разность между полученным при измерении значением величины и ее истинным (или действительным) значением. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина. Зная только абсолютную погрешность измерений нельзя судить о качестве – точности проведённого измерения.

Относительная погрешность измерения – погрешность измерения, выраженная отношением модуля абсолютной погрешности измерения к истинному (или действительному) значению измеряемой величины;

.

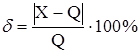Относительная погрешность выражается в процентах или в безразмерных единицах. Значение относительной погрешности позволяет судить о точности проведённого измерения.

Приведённая погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому нормирующему значению, постоянному во всем диапазоне измерений или его части.

,

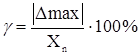где Х_n – нормирующее значение. В качестве нормирующего значения используют предел измерения прибора.

По зависимости погрешности от значений измеряемой величины погрешности бывают:

Аддитивная погрешность – это погрешность, не зависящая от измеряемой величины (рис. 1.а);

Мультипликативная погрешность – это погрешность, которая прямо пропорциональна измеряемой величине (рис.1.б);

Нелинейная погрешность – это погрешность, которая имеет нелинейную зависимость от измеряемой величины (рис. 1.в).

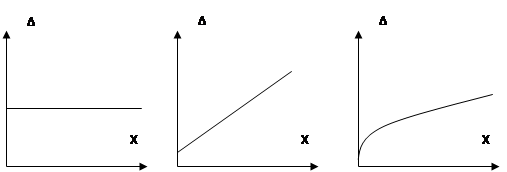
Рисунок 1. Зависимость погрешности от измерения величины.

По характеру проявления погрешности делятся:

Случайная погрешность – это составляющая погрешности измерения, связанная с факторами, которые изменяются при повторных измерениях хаотически, носят нерегулярный характер и их трудно предвидеть. Иногда подобные изменения проявляются очень сильно, например, при резком однократном изменении напряжения питания прибора. В этом случае погрешность значительно превышает границы, определяемые ходом процесса измерений в целом и ее называют грубой погрешностью или промахом.

Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя.

В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей:

1. Погрешности метода, или теоретические погрешности, возникающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений;

2. Инструментальные погрешности, возникают из-за собственной погрешности средства измерения, определяемой классом точности, влиянием средства измерения на результат и его ограниченной разрешающей способностью;

3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и так далее;

4. Личные погрешности, связаны с индивидуальными особенностями наблюдателя.

Рассмотрим примеры задач связанных с обзором погрешностей измерений.

Задача 1. Для вольтметра с пределом измерения на 500 В с классом точности 1,5 определить максимальную абсолютную погрешность. Сравнить точность измерения этим вольтметром на напряжение 100 вольт и 500 вольт.

Решение задачи.

Класс точности прибора это его приведённая погрешность. Следовательно, максимальная абсолютная погрешность выражается из формулы . .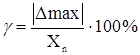

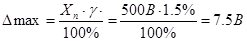Для того чтобы оценить точность измерений необходимо найти относительную погрешность для указанных напряжений, при условии, что абсолютную погрешность мы нашли предыдущим действием:

.

.

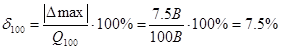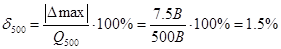Таким образом, при 500 измерении 500 вольт точность получается больше.

Задача 2. Определить соответствует ли амперметр с пределом измерения на 5Ампер с классом точности 1,5 своему классу точности. Если при проведении его поверки образцовым амперметром были получены следующие показания:

Решение задачи.

Для того чтобы определить соответствует ли амперметр своему классу точности необходимо определить приведённую погрешность прибора и если она меньше класса точности прибора, то прибор соответствует своему классу точности.

Абсолютная погрешность это разность между показаниями испытуемого прибора и образцового. Из таблицы видно, что максимальная абсолютная погрешность будет равна .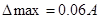

Тогда приведённая погрешность будет находиться следующим образом:

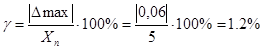. Таким образом, приведённая погрешность меньше класса точности прибора, а значит, прибор соответствует своему классу точности.

Задача 3. Определить какой из двух приборов измеряет ток 200мкА точнее РА1 = класс точности 0,2 предел 300мкА.

РА2 = класс точности 0,1 предел 1мА.

Решение задачи.

Необходимо для каждого прибора рассчитать относительную погрешность для измерения указанного в условии тока. Для этого необходимо рассчитать максимальную абсолютную погрешность для каждого из приборов через формулу для приведённой погрешности.

.

.

.

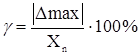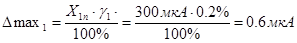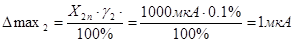Далее найдёт для каждого прибора относительную погрешность:

.

.

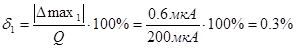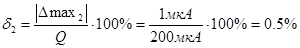Таким образом, первый прибор измеряет точнее.