РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
Математика
| Направление: | 21.03.02 «Землеустройство и кадастры» |
| Профили: | Землеустройство |
| Уровень подготовки | Бакалавриат |
Курс 1
Семестры 1-2
Калуга, 2016
Составители: к. п. н., доцент Жукова И.С « » 2016г.
Программа разработана в соответствии с ФГОС ВО по направлению подготовки 21.03.02 «Землеустройство и кадастры». Рабочая программа дисциплины соответствует учебному плану 2016 г. начала подготовки.
Программа обсуждена на заседании кафедры «Высшей математики и экономической кибернетики»
Зав. кафедрой Мишин П.Н., к.э.н., доцент
протокол № « » 2016г.
Проверено:
Начальник УМЧ _____________________доцент О.А. Окунева
Лист согласования рабочей программы
Декан агрономического факультета
к.биол.н. , доцент Малахова С.Д.
« » 2016г.
Программа принята учебно-методической комиссией по направлению подготовки
21.03.02 “ Землеустройство и кадастры”, протокол № ____
Председатель учебно-методической комиссии по направлению подготовки
Сихарулидзе Т.Д., доцент , к. с-х. н. « » 2016г
Заведующий выпускающей кафедрой Слипец А.А., к.биол.н., доцент
« » 2016г
Оглавление
Аннотация……………………………………………………………………………… 5
1. Требования к уровню освоения дисциплины и ее место в структуре образовательной программы…………………………………………………………… 6
1.1.Требования к уровню освоения дисциплины (планируемые результаты обучения) …………………………………………………………………………………………… 6
1.2. Место дисциплины в структуре образовательной программы…………… …… 6
2. Цели и задачи дисциплины. Требования к результатам освоения дисциплины.6
3. Организационно-методические данные дисциплины (виды учебной работы и их трудоемкость)………………………………………………………………………….. 7
4. Структура и содержание дисциплины…………………………………………………… 8
4.1Структура дисциплины……………………………………………………….……. .8
4.2. Трудоёмкость разделов и тем дисциплины…………………………………… 13
4.3.Содержание разделов дисциплины………………………........................ ...17
4.4. Лабораторные/ практические/ семинарские занятия …………………..…… ....20
4.5. Самостоятельное изучение разделов дисциплины……………………………………… …36
4.5.1. Перечень вопросов для самостоятельного изучения………………………………………36
4.5.2. Курсовые проекты (работы)/ контрольные работы/ расчетно-графические работы/ учебно-исследовательские работы………………………………………………………………………………43
5. Взаимосвязь видов учебных занятий……………………………………………. ..45
6. Учебно-методическое и информационное обеспечение дисциплин 45
6.1. Основная литература …………………………………………………………………………… 45
6.2. Дополнительная литература………………………………………………………………… 45
6.3. Методические указания, рекомендации и другие материалы к занятиям.. ………46
6.4 Интернет-ресурсы……………………………………………………………………….46
7. Критерии оценки знаний, умений, навыков и заявленных компетенций .. 47
8. Материально-техническое обеспечение дисциплины………………………………….52
9. Методические рекомендации преподавателям по организации обучения дисциплины.53
10.Методические рекомендации студентам по самостоятельной работе………………..53
Аннотация
. В рабочей программе отражены темы теоретических основ математики применительно к профессиональной подготовке 21.03.02 “ Землеустройство и кадастры”. Предмет математика служит фундаментальной базой вузовского образования. Он содержит вопросы алгебры, геометрии, математического анализа, теории вероятностей, численных методов. Основы геометрии, алгебры, являющиеся фундаментальными основами картографии и геодезии. В рабочей программе рассматриваются классические способы определения координат точек на основе формул аналитической геометрии и численных методов. Приводятся способы определения площадей земной поверхности на основе основных положений математического анализа.
Студентам предлагается для изучения теория наилучшего приближения функции с помощью многочленов, создателем которой является русский математик П.Л. Чебышев, которая в настоящее время является могучим средством исследования. Все это позволит теорию и методику определения площадей земельных участков, создания топографических карт и кадастровых расчетов к ним поставить на высокую научную основу. Вопросы численных методов, в частности задачи оптимизации, изучающиеся на основе симплекс-метода, метода Жордана-Гаусса, метода Франке-Вулфа и штрафных функций позволят будущему специалисту определять координаты оптимальной точки не только на плоскости, но и в пространстве. Это позволит будущему специалисту разбираться в вопросах применимости математики как к землеустройству и кадастровым расчетам, так и к вопросам управления персоналом, в вопросах экономической эффективности, плановости предприятия, на котором ему придется работать, к возможности применения в работе средств вычислительной техники.
Изучение элементов теории вероятностей и математической статистики, методики расчета погрешности результатов измерений, конкретное построение доверительных интервалов для измеряемой величины, исследование линейной корреляции переменных величин, методов предельного перехода обеспечивает подготовку студентов для исследовательских проектов.
Изучение всех, выше указанных сложных математических приемов не возможно без серьезной математической подготовки. Это налагает большую ответственность на студентов, изучающих этот курс.
Вместе с тем, в процессе учебной деятельности через предмет математика студент совершенствует свое личностное развитие: успехи в учебе способствуют повышению уровня личных притязаний, решение сложных задач способствует умению работать в коллективе, объективно относиться к своим ошибкам. При выборе правильных, рациональных методов, приемов, средств учебной работы со студентом приоритетным направлением является рассмотрение тех компетенций, которые необходимо приобрести студенту в ходе его профессиональной подготовки.
1. Требования к уровню освоения дисциплины и ее место
в структуре образовательной
Программы
1.1. Требования к уровню освоения дисциплины (планируемые результаты обучения)
Реализация в дисциплине «математика» требований ФГОС ВО, ОПОП ВО и Учебного плана по направлению подготовки 21.03.02 “ Землеустройство и кадастры» должна формировать следующие компетенции:
(ОК-7)- способностью к самоорганизации и самообразованию;
(ПК-6) – способностью проведения и анализа результатов исследований и новых разработок.
|
|
Предлагаемый компетентностный подход, рассматривая, возможность формирования у студентов выше указанных компетенции предусматривает, что студент владеет культурой мышления, обладает способностью к восприятию, обобщению и анализу информации, умеет логически верно, аргументировано и ясно формулировать свою мысль.
1.2. Место дисциплины в структуре образовательной программы.
Предшествующими курсами, на которых непосредственно базируется дисциплина «математика» является школьный курс математики.
Дисциплина «матаматика» является основополагающим для изучения следующих дисциплин: экономико-математические методы и моделирование, прикладная геодезия. Особенностью дисциплины является научность, возможность применения математических методов для методики определения площадей земельных участков, создания топографических карт и кадастровых расчетов.
Контроль знаний студентов проводится в форме текущей и промежуточной аттестации. Текущая аттестация студентов – оценка знаний и умений проводится постоянно на практических занятиях при решении студентами задач у доски, с помощью тестовых заданий, контрольных работ, письменного опроса и оценки индивидуальных заданий.
Промежуточная аттестация студента проводится в форме зачета в 1-м семестре и в форме экзамена – во 2-м семестре.
2. Цели и задачи дисциплины. Требования к результатам освоения дисциплины.
Целью дисциплины «математика» является освоение студентами теоретических и практических знаний и приобретение умений и навыков в области математики для дальнейшего применения этих знаний и навыков учебной работы в изучении дисциплин профессиональной направленности.
Внутренние требования: В результате изучения дисциплины «Математика» студент должен:
Знать: - основные понятия и инструменты алгебры и геометрии и методов математического анализа теории вероятностей и математической статистики и численных методов, позволяющих теорию и методику определения площадей земельных участков, создания топографических карт и кадастровых расчетов к ним поставить на высокую научную основу.
Уметь: -систематизировать учебный материал при работе с литературой; уметь своевременно выполнять задания и осуществлять подготовку к письменному опросу и контрольным работам;
- решать типовые математические задачи применительно к вопросам с/.х. производства:
-обрабатывать эмпирические и экспериментальные данные и делать выводы (определять коэффициенты корреляции методом наименьших квадратов и строить математическую модель линейной и нелинейной зависимости);
-использовать методики расчета погрешности результатов измерений, конкретное построение доверительных интервалов для измеряемой величины, исследование линейной корреляции переменных величин, уметь использовать методы предельного перехода;
-определять площади земной поверхности;
-с помощью методов Жордана-Гаусса, метода Франке-Вулфа и штрафных функций определять координаты оптимальной точки не только на плоскости, но и в пространстве.
Владеть: - культурой мышления, обладает способностью к восприятию, обобщению и анализу информации;
- основными приёмами обработки экспериментальных данных
- методами математического анализа; математическими, количественными методами решения типовых профессиональных задач (находить экстремум функции одной и двух переменных, находить и строить асимптоты к графику функции; методом хорд и касательных и другими численными методами)
- методами проверки гипотез, статистическими методами обработки экспериментальных данных.
3. Организационно-методические данные дисциплины (виды учебной работы и их трудоемкость)
Общая трудоёмкость дисциплины составляет 5зач.ед. (189часов), их распределение по видам работ и по семестрам представлено в таблице 1
Таблица 1
| Вид учебной работы | Трудоемкость | |||
| зач. ед. | час. | по семестрам | ||
| №1 | №2 | |||
| Общая трудоемкость дисциплины по учебному плану | 5 | 216 | 108 | 108 |
| Аудиторные занятия | 4 | 144 | 72 | 72 |
| Лекции (Л) | 1 | 36 | 18 | 18 |
| Практические занятия (ПЗ) | 3 | 108 | 54 | 54 |
| Семинары (С) | ||||
| Лабораторные работы (ЛР) | ||||
| Самостоятельная работа (СРС) | 1.25 | 45 | 36 | 9 |
| в том числе: | ||||
| консультации | ||||
| контрольные работы | 0.25 | 9 | 4.5 | 4.5 |
| др. виды | ||||
| Вид контроля: | ||||
| зачет | 0.25 | 9 | + | |
| экзамен | 0,75 | 27 | + | |
| зачет | экзамен | |||
Курс рассчитан на 216 часов, из них – 144аудиторных часа (36 часов лекций , 108 часа практических занятий), 45 часов самостоятельной работы, экзамен-27 часов.
*Применение активных и интерактивных образовательных технологий в учебном процессе приведены в таблице № 2 приложения.
4.Структура и содержание дисциплины.
4.1 Структура дисциплины.
4.1. Структура дисциплины
| Дисциплина «Математика» | |
| Раздел 1 Линейная алгебра | Раздел 7 Функции нескольких переменных - |
| Раздел 2. Векторная алгебра | Раздел 8– Комплексные числа |
| Раздел 3 – Аналитическая геометрия на плоскости и в пространстве | Раздел 9 – Численные методы. |
| Раздел 4– Функции и пределы | Раздел 10 – Дифференциальные уравнения |
| Раздел 5 – Производная и ее применение | Раздел 11 – Ряды |
| Раздел 6 - Неопределенный и определенный интеграл. | Раздел 12 Теория вероятностей и математическая статистика. |
Рисунок 1 – Содержание разделов дисциплины «математика»
Содержание разделов дисциплины
| |||||||||||||||||||||||||
Рисунок 2 – Раздел 1. «Линейная алгебра»
| Раздел 2 – Векторная алгебра | ||||
| Тема 7. Векторы. Линейные операции над ними. Разложение векторов | Тема 8. Операции над векторами. Евкидово пространство. | |||
Рисунок 3 – Раздел 2. «Векторная алгебра»
| Раздел 3 – Аналитическая геометрия на плоскости и в пространстве | |||||||
|
|
| ||||||
| Тема 9. Метод координат на плоскости. Прямая на плоскости | Тема10. Кривые второго порядка | Тема 11.Аналитическая геометрия в пространстве | |||||
Рисунок 4 – Раздел 3. «Аналитическая геометрия на плоскости и в пространстве»
| Раздел 4– Функции и пределы | |||||||
|
|
| ||||||
| Тема 12. Функции и их графики. Последовательности. Предел числовой последовательности . | Тема 13. Предел функции. Непрерывность функции. Асимптоты. | Тема 14.Методы вычисления пределов. | |||||
Рисунок 5 – Раздел 4. «Функции и пределы»
| Раздел 5 – Производная и ее применение | |||||||
|
|
| ||||||
| Тема15. Производная и дифференциал функции. | Тема16.Исследование функций и построение графиков. Выпуклость функции. | Тема17.Применение производной в вопросах с-х. производства. | |||||
Рисунок 6 – Раздел 5. «Производная и ее применение»
| Раздел 6 – Неопределенный и определенный интеграл. | ||||
| Тема 18. Важнейшие свойства и основные методы интегрирования неопределенных интегралов. | Тема 21.Несобственные интегралы. | |||
| Тема 19.Интегрирование рациональных дробей. | Тема22. Приложения определенного интеграла к решению вопросов с-х. производства. | |||
| Тема 20.Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов. | ||||
Рисунок 7 – Раздел 6. «Неопределенный и определенный интеграл»
| Раздел 7– Функции нескольких переменных | |||||||
|
|
| ||||||
| Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных.
| Тема 24.Условный экстремум функции двух переменных. | Тема 25.Производная по направлению. Градиент функции. | |||||
Рисунок 9 – Раздел 8. «Функции нескольких переменных»
| Раздел 8– Комплексные числа | |||||||
|
|
| ||||||
| Тема 26. Комплексные числа. Основные действия над комплексными числами.
| Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера.
| Тема 28. Разложение многочлена на множители в случае комплексных корней.
| |||||
Рисунок 10 – Раздел 9. « Комплексные числа»
| Раздел 9 – Численные методы | ||||
| Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. | Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона. | |||
| Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. | Тема 34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. | |||
| Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол. | Тема35. Метод Франка-Вулфа. Метод штрафных функций. | |||
| Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. | Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. | |||
Рисунок 11 – Раздел 10. «Численные методы»
| Раздел 10 – Дифференциальные уравнения | ||||
| Тема 37. Дифференциальные уравнения с разделяющимися неизвестными. | Тема 40. Линейные дифференциальные уравнения первого порядка. Метод Лагранжа. | |||
| Тема 38. Однородные дифференциальные уравнения первого порядка. | Тема 41. Дифференциальные уравнения первого порядка в полных дифференциалах. | |||
| Тема 39. Линейные дифференциальные уравнения первого порядка. Метод Бернулли. | Тема 42. Дифференциальные уравнения в вопросах с-х. производства. | |||
Рисунок 12 – Раздел 11. «Дифференциальные уравнения»
| Раздел 11– Ряды | |||||||
|
|
| ||||||
| Тема 43. Числовые ряды. Основные понятия. Признаки сходимости.
| Тема 44. Степенные ряды. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд Тейлора (Маклорена) | Тема 45. Гармонический анализ. Ряды Фурье. | |||||
Рисунок 12 – Раздел 11. «Ряды»
| Раздел 12 – Теория вероятностей и математическая статистика | ||||
| Тема 46.Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. Теоремы сложения и умножения вероятностей. | Тема 52. Статистические оценки параметров распределения. Точечные и интервальные оценки. | |||
| Тема 47. Формула полной вероятности. Формула Байеса. | Тема 53.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов. | |||
| Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа. | Тема 54. Линейная регрессия со сгруппированными данными в задачах с-х производства. | |||
| Тема 49. Случайные величины. Дискретная случайная величина. Законы распределения. Числовые характеристики. | Тема 55Линейная регрессия с несгруппированными данными. | |||
| Тема 50. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Показательное и равномерное распределения. |
Тема 56. Дисперсионный анализ в задачах инженерии. | |||
| Тема 51.Основы математической статистики. Выборочный метод Основные выборочные характеристики статистического распределения. | Тема 57. Многомерный кластерный анализ. | |||
Рисунок 13 – Раздел 12. «Теория вероятностей и математическая статистика »
4.2. Трудоёмкость разделов и тем дисциплины
Таблица 2 - Трудоемкость разделов и тем дисциплины
Наименование
Разделов и тем дисциплины
Всего часов на раздел/тему
Аудиторная
Работа
Внеаудиторная работа (СРС)
* Применение активных и интерактивных образовательных технологий представлено в ПРИЛОЖЕНИИ 1.
4.3. Содержание разделов дисциплины
1 СЕМЕСТР
Раздел 1.Линейная алгебра
Тема 1. Матрицы. Операции над матрицами. Определители. Вычисление определителей.
Тема 2. Ранг матрицы. Приведение матрицы к ступенчатому виду. Обратная матрица. Матричные уравнения.
Тема 3. Системы линейных уравнений. Метод обратной матрицы.
Тема 4. Метод Крамера.
Тема 5. Метод Гаусса. Метод Жордана-Гаусса.
Тема 6. Понятие разрешенных и свободных переменных системы. Теорема Кронекера-Капелли.
Раздел 2. Векторная алгебра.
Тема 7.Векторы. Линейные операции над ними. Разложение векторов.
Тема 8. Операции над векторами.
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Евклидово пространство.
Раздел 3. Аналитическая геометрия на плоскости и в пространстве.
Тема 9. Метод координат на плоскости. Деление отрезка в данном отношении. Расстояние от точки до прямой. Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой через две точки, каноническое уравнение прямой, уравнение прямой в отрезках на осях. Угол между двумя прямыми.
Тема 10. Кривые второго порядка. Эллипс. Гипербола. Парабола.
Тема 11.Аналитическая геометрия в пространстве.
Раздел 4. Функции и пределы.
Тема 12.Математические модели. Множества. Функции и их графики. Последовательности. Свойства числовых множеств и последовательностей. Предел числовой последовательности.
Тема 13. Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты.
Тема 14.Методы вычисления пределов.
Раздел 5. Производная и ее применение.
Тема 15. Производная и дифференциал функции.
Тема 16.Исследование функций и построение графиков. Выпуклость функции. Точка перегиба функции.
Тема 17. Применение производной в вопросах с-х. производства.
Раздел 6. Неопределенный и определенный интеграл.
Тема 18.Важнейшие свойства и основные методы интегрирования неопределенных интегралов.
Тема19.Интегрирование рациональных дробей.
Тема 20. Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов.
Тема 21. Несобственные интегралы.
Тема 22. Применение интегрального исчисления к вопросам с-х. производства.
2 СЕМЕСТР
Раздел 7. Функции нескольких переменных.
Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных.
Тема 24. Условный экстремум функции двух переменных.
Тема 25.Производная по направлению. Градиент функции.
Раздел 8.
Комплексные числа.
Тема 26. Комплексные числа. Сопряженные комплексные числа. Модуль
комплексного числа. Геометрическая интерпретация комплексного числа.
Основные действия над комплексными числами.
Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера.
Тема 28. Разложение многочлена на множители в случае комплексных корней.
Раздел 9. Численные методы.
Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона.
Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева.
Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы .Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол.
Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения.
Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона.
Тема 34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод.
Тема 35. Метод Франка-Вулфа. Метод штрафных функций.
Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений.
3 СЕМЕСТР
Раздел 10.Дифференциальные уравнения.
Тема 37.Дифференциальные уравнения первого порядка с разделяющимися неизвестными.
Тема 38. Однородные дифференциальные уравнения первого порядка.
Тема 39. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.
Тема 40. Линейные дифференциальные уравнения первого порядка. Метод Лагранжа.
Тема 41. Дифференциальные уравнения первого порядка в полных дифференциалах.
Тема 42. Дифференциальные уравнения в вопросах с-х. производства.
Раздел 11. Ряды.
Тема 43. Числовые ряды. Основные понятия. Признаки сходимости.
Тема 44. Степенные ряды. Ряды Тейлора и Маклорена . Разложение
элементарных функций в ряд Тейлора (Маклорена).
Тема 45. Гармонический анализ. Ряды Фурье.
Раздел 12. Теория вероятностей и математическая статистика.
Тема 46. Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. Теоремы сложения и умножения вероятностей.
Тема 47. Формула полной вероятности. Формула Байеса.
Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа.
Тема49.Случайные величины. Дискретная случайная величина. Законы распределения.
Биномиальное распределение, распределение Пуассона, Лапласа. Понятие наивероятнейшего числа испытаний. Закон больших чисел в формуле Чебышева. Числовые характеристики.
Тема 50. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Правило трёх сигм.
Показательное и равномерное распределения непрерывной случайной величины.
Тема 51. Основы математической статистики. Выборочный метод. Основные выборочные характеристики статистического распределения.
Тема 52. Статистические оценки параметров распределения. Точечные и интервальные оценки.
Тема53.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов.
Тема 54. Линейная регрессия со сгруппированными данными в задачах с-х производства.
Тема 55.Линейная регрессия с несгруппированными данными.
Тема 56.Дисперсионный анализ в вопросах землеустройства и кадастровых расчетах.
Тема 57.Многомерный кластерный анализ.
Раздел 1. Линейная алгебра.
2.
Раздел 2. Векторная алгебра.
3.
Раздел 3. Аналитическая геометрия на плоскости и в пространстве.
4.
Раздел 4. Функции и пределы
5.
Раздел 11.Ряды.
11.
Раздел 12. Теория вероятностей и математическая статистика
Всего за второй семестр
Всего за год
4.5Самостоятельное изучение разделов дисциплины
4.5.1 Перечень вопросов для самостоятельного изучения
Таблица 4 - Перечень вопросов для самостоятельного изучения
| № п/п | № раздела и темы дисциплины | Перечень рассматриваемых вопросов для самостоятельного изучения |
Кол-во | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. |
Раздел 1. Линейная алгебра. | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 1 . Матрицы. Операции над матрицами. Определители. Вычисление определителей. | Матрицы. Операции над матрицы. Обратная матрица. Определители. Вычисление определителей.
| 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 2. Ранг матрицы. Приведение матрицы к ступенчатому виду. Обратная матрица. Матричные уравнения. | Ранг матрицы. Методы вычисления ранга матрицы. | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 3. Системы линейных уравнений. Понятие разрешенных и свободных переменных систем Метод обратной матрицы | Понятие разрешенных и свободных переменных системы. Метод обратной матрицы. | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 4. Метод Крамера. | Метод Крамера.
| 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 6. Теорема Кронекера-Капелли. |
Теорема Кронекера-Капелли. | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | Раздел 2. Векторная алгебра. | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 7. Векторы. Линейные операции над векторами. | Векторы. Линейные операции над ними. Разложение векторов. Базис векторного пространства.
| 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 8. Скалярное, векторное и смешанное произведение векторов. Евклидово пространство. | Скалярное, векторное и смешанное произведение векторов. Евклидово пространство. | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | Раздел 3. Аналитическая геометрия на плоскости и в пространстве. | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 9. Метод координат на плоскости. Прямая на плоскости. | Метод координат на плоскости. Деление отрезка в данном отношении. Расстояние от точки до прямой. Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой через две точки. Угол между двумя прямыми. Векторное, параметрическое и каноническое уравнение прямой | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 10.Кривые второго порядка | Эллипс. Гипербола. Парабола.
| 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 11. Аналитическая геометрия в пространстве. | Метод координат в пространстве. Плоскость в пространстве. Положение прямой и плоскости в пространстве. | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. |
Раздел 4. Функции и пределы | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 12. Математические модели. Множества. Функции и их графики. Последовательности. Свойства числовых множеств и последовательностей. Предел числовой последовательности.
| Множества. Функции и их графики. Последовательности. Предел числовой последовательности. |
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 13. Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты. | Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 14. Методы вычисления пределов | Предел функции. Раскрытие неопределенностей. Понятие бесконечно-больших, бесконечно-малых величин. | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5.
|
Раздел 9.Численные методы. | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема29.Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. | Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. | Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 31.Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол. | Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. | Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона. | Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона. | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. | Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема35. Метод Франка-Вулфа. Метод штрафных функций. | Метод Франка-Вулфа. Метод штрафных функций.
| 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. | Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интернет ресурсы. 1.http:// www. intuit. ru/ 2.http://www. edu.ru/ 3.http://www.i-exam.ru/ 4.http://www.allmath.ru/ 6.3 Методические указания, рекомендации и другие материалы к занятиям · Методические рекомендации для самостоятельной работы студентов. · Комплекты задач по тематикам. · Глоссарий. · Варианты контрольных работ · Тесты · Индивидуальные домашние задания Паспорт фонда оценочных средств по дисциплине «Математика»
Приложение- 3
Проверочные тесты . Задания под пунктом а) для первого варианта, под пунктом б) -для второго варианта
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ Задания приводятся в той форме, которую студенты видят на экране компьютера во время проведения тестирования. Слева от вертикальной черты расположены условия заданий, справа — варианты ответа. Правильный вариант (или варианты) ответа отмечен точкой. Некоторые тестовые задания требуют от студента ввести ответ или расставить соответствия между математическими объектами, стоящими справа и слева от вертикальной черты. Задание 1.
Задание 2. Дана функция
Тогда ее областью определения является . Задание 3
По формулам Крамера решить систему:
а) б)
Задание 4
Методом Гаусса решить систему:
а) б)
Задание 5 . а) Если 1) б)Если 1)
Задание 6
а) Даны векторы
Их скалярное произведение
в) Их скалярное произведение
Задание 7 а) В треугольнике с вершинами длина высоты, опущенной из вершины С на сторону АВ составит:
в) В треугольнике с вершинами длина высоты, опущенной из вершины С на сторону АВ составит:
Задание 8
Предел функции равен:
а) 1. 2.
А)в) 1. 1) 4; 2) 1/4; 3) 8/5; 4)0.5 2. 1)4; 2) 2; 3) -3 4) 0 Задание 9 Точками экстремума функций а) y=x
б)y=x Задание 10
а) Угловой коэффициент прямой 6x + 2y – 5 = 0 равен … 1) 3 2) −6 3) 2 4) −3. в) Угловой коэффициент прямой 6x + 3y – 2 = 0 равен … 1) 3 2) −6 3) -2 4) −3.
) Задание 11
а) Координата x0 точки А(х0; 1; 7), принадлежащей плоскости 5x + y – z + 1 = 0, равна … 1) 4; 2) 1; 3) 3; 4) 2. б) Координата x0 точки А(х0; 1; 7), принадлежащей плоскости 3x - y +3 z + 1 = 0, равна … 1) 4; 2) -7; 3) 3; 4) 2.
) Задание 12
а)Производная функции 1)
. б) Производная произведения xex равна … 1) ) Задание 1 3
а) В урне 4 белых и 6 черных шаров. Из урны вынимают сразу 2 шара. Вероятность того, что шары разного цвета, равна... 1) 8/15; 2) 1; 3) 3/5; 4) 1/24. , б) Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и ВТО рого стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна… 1) 0,28; 2) 0,15; 3) 0,9; 4) 0,18. ) Задание 1 4 Вычислить площадь фигуры, ограниченной линиями: а)y=x2-4x+3, y=x-1. б). y=x2-2x-1, y=x-1.
Приложение -4 Заочное отделение. Год начала подготовки 2016, образовательный стандарт 1084 от 01.10.25 4.5 лет подготовки
Общая трудоёмкость дисциплины составляет 6зач.ед. (216часов), их распределение по видам работ и по семестрам представлено в таблице 1 Таблица 1
Курс рассчитан на 216часов, из них – 12аудиторных часа (4часов лекций , 8 часа практических занятий), 195 часов самостоятельной работы, экзамен-9часов.
Трудоёмкость разделов и тем дисциплины Таблица 2 - Трудоемкость разделов и тем дисциплины Наименование Разделов и тем дисциплины |
Всего часов на раздел/тему |
Аудиторная Работа |
Внеаудиторная работа (СРС) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Л | ЛПЗ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1-й семестр | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 1.Линейная алгебра | 10 | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 1. Матрицы. Операции над матрицами. Определители. Вычисление определителей. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 2. Ранг матрицы. Приведение матрицы к ступенчатому виду. 21.09 пр. Обратная матрица. Матричные уравнения. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 3. Системы линейных уравнений. Метод обратной матрицы. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 4. Метод Крамера. Тема 5. Метод Гаусса. Метод Жордана-Гаусса. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 6. Понятие разрешенных и свободных переменных системы. Теорема Кронекера-Капелли | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 2. Векторная алгебра | 13 | 1 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 7.Векторы. Линейные операции над ними. Разложение векторов. | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 8.Операции над векторами. Евклидово пространство. | 7 | 1 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 3. Аналитическая геометрия на плоскости и в пространстве. | 13 | 1 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 9. Метод координат на плоскости. .Прямая на плоскости. | 7 | 1 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема10.Кривые второго порядка. Тема 11.Аналитическая геометрия в пространстве | 6 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 4. Функции и пределы | 16 | 16 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 12.Математические модели. Множества. Функции и их графики. Последовательности. Свойства числовых множеств и последовательностей. Предел числовой последовательности. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 13. Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты. Тема 14. Методы вычисления пределов. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 5. Производная и ее применение. | 12 | 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 15. Производная и дифференциал функции. | 4 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 16. Исследование функций и построение графиков. Выпуклость функции. | 4 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 17.Применение производной в вопросах с-х. производства. | 4 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 6. Неопределенный и определенный интеграл. | 30 | 2 | 28 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 18.Важнейшие свойства и основные методы интегрирования неопределенных интегралов. Тема 19. Интегрирование рациональных дробей. | 6 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 20. Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов. | 11 | 1 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 21. Несобственные интегралы | 4 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 22. Приложения определенного интеграла к решению вопросов с-х. производства. | 9 | 1 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Самоподготовка к текущему контролю+зачет | 90 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего за 1семестр | 94 | 2 | 2 | 90 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2-й семестр | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 7. Функции нескольких переменных. | 13 | 2 | 1 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных. | 6 | 1 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 24.Условный экстремум функции двух переменных. Тема 25.Производная по направлению. Градиент функции. | 7 | 1 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 8. Комплексные числа. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 26. Комплексные числа. Основные действия над комплексными числами. Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера. Тема 28. Разложение многочлена на множители в случае комплексных корней. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 9. Численные методы. | 32 | 2 | 30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол. | 11 | 1 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона | 11 | 1 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. Тема35. Метод Франка-Вулфа. Метод штрафных функций. Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений | 10 | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 10. Дифференциальные уравнения первого порядка. | 26 | 26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 37. Дифференциальное уравнение первого порядка с разделяющимися неизвестными. Тема38.Однородные дифференциальные уравнения первого порядка. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 39. Линейное дифференциальное уравнение первого порядка. Метод Бернули. Тема 40. Линейное дифференциальное уравнение первого порядка. Метод Лагранжа. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 41. Дифференциальные уравнения первого порядка в полных дифференцилах. Тема 42. Дифференциальные уравнения в вопросах с-х. производства. | 10 | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел 11. Ряды. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 43. Числовые ряды. Основные понятия. Признаки сходимости. Тема 44. Степенные ряды. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд Тейлора (Маклорена) Тема 45. Гармонический анализ. Ряды Фурье. | 8 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Раздел12. Теория вероятностей и математическая статистика | 26 | 2 | 2 | 22 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 46. Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 47. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. | 3 | 1 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа. | 3 | 1 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема49.Случайные величины. Дискретная случайная величина. Законы распределения. Тема50.Числовые характеристики. Неравенство Чебышева. Закон больших чисел. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 51. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Показательное и равномерное распределения. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 52. Основы математической статистики. Выборочный метод Основные выборочные характеристики статистического распределения | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 53. Статистические оценки параметров распределения. Точечные и интервальные оценки. | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 54.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов | 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 55. Линейная регрессия со сгруппированными данными в задачах с-х производства Линейная регрессия с несгруппированными данными. | 3 | 1 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема 56.Дисперсионный анализ в анализ в вопросах землеустройства и кадастровых расчетах. Тема 57.Многомерный кластерный анализ. | 5 | 1 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Самоподготовка к текущему контролю | 113 | 2 | 6 | 105 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Подготовка к экзамену | 9 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего за 2 семестр. | 122 | 2 | 6 | 114 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Итого за учебный год | 216 | 4 | 8 | 204 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приложение -5 Заочное отделение. Год начала подготовки 2016, образовательный стандарт 1084 от 01.10.25 3.5 лет подготовки
Общая трудоёмкость дисциплины составляет 6зач.ед. (216часов), их распределение по видам работ и по семестрам представлено в таблице 1
Таблица 1 -
| Вид учебной работы | Трудоемкость | |||
| зач. ед. | час. | по семестрам | ||
| №1 | №2 | |||
| Общая трудоемкость дисциплины по учебному плану | 6 | 216 | 108 | 108 |
| Аудиторные занятия | 4 | 8 | 4 | 4 |
| Лекции (Л) | 4 | 2 | 2 | |
| Практические занятия (ПЗ) | 4 | 2 | 2 | |
| Семинары (С) | ||||
| Лабораторные работы (ЛР) | ||||
| Самостоятельная работа (СРС) | 5.52 | 199 | 104 | 95 |
| в том числе: | ||||
| консультации | ||||
| самоподготовка к текущему контролю знаний | 5.52 | 199 | 104 | 95 |
| др. виды | ||||
| Вид контроля: | ||||
| зачет | + | |||
| экзамен | 0,25 | 27 | 9 | |
| зачет | экзамен | |||
Курс рассчитан на 216 часов, из них – 8аудиторных часа (4часов лекций , 4часа практических занятий), 199часов самостоятельной работы, экзамен-9 часов.
Трудоёмкость разделов и тем дисциплины
Таблица 2 - Трудоемкость разделов и тем дисциплины
|
Наименование Разделов и тем дисциплины |
Всего часов на раздел/тему |
Аудиторная Работа |
Внеаудиторная работа (СРС) | |
| Л | ЛПЗ | |||
| 1-й семестр | ||||
| Раздел 1.Линейная алгебра | 24 | 24 | ||
| Тема 1. Матрицы. Операции над матрицами. Определители. Вычисление определителей. | 4 | 4 | ||
| Тема 2. Ранг матрицы. Приведение матрицы к ступенчатому виду. 21.09 пр. Обратная матрица. Матричные уравнения. | 4 | 4 | ||
| Тема 3. Системы линейных уравнений. Метод обратной матрицы. | 4 | 4 | ||
| Тема 4. Метод Крамера. Тема 5. Метод Гаусса. Метод Жордана-Гаусса. | 4 | 4 | ||
| Тема 6. Понятие разрешенных и свободных переменных системы. Теорема Кронекера-Капелли | 8 | 8 | ||
| Раздел 2. Векторная алгебра | 13 | 1 | 12 | |
| Тема 7.Векторы. Линейные операции над ними. Разложение векторов. | 6 | |||
| Тема 8.Операции над векторами. Евклидово пространство. | 7 | 1 | 6 | |
| Раздел 3. Аналитическая геометрия на плоскости и в пространстве. | 13 | 1 | 12 | |
| Тема 9. Метод координат на плоскости. .Прямая на плоскости. | 7 | 1 | 6 | |
| Тема10.Кривые второго порядка. Тема 11.Аналитическая геометрия в пространстве | 6 | 6 | ||
| Раздел 4. Функции и пределы | 16 | 16 | ||
| Тема 12.Математические модели. Множества. Функции и их графики. Последовательности. Свойства числовых множеств и последовательностей. Предел числовой последовательности. | 8 | 8 | ||
| Тема 13. Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты. Тема 14. Методы вычисления пределов. | 8 | 8 | ||
| Раздел 5. Производная и ее применение. | 12 | 12 | ||
| Тема 15. Производная и дифференциал функции. | 4 | 4 | ||
| Тема 16. Исследование функций и построение графиков. Выпуклость функции. | 4 | 4 | ||
| Тема 17.Применение производной в вопросах с-х. производства. | 4 | 4 | ||
| Раздел 6. Неопределенный и определенный интеграл. | 30 | 2 | 28 | |
| Тема 18.Важнейшие свойства и основные методы интегрирования неопределенных интегралов. Тема 19. Интегрирование рациональных дробей. | 6 | 6 | ||
| Тема 20. Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов. | 11 | 1 | 10 | |
| Тема 21. Несобственные интегралы | 4 | 4 | ||
| Тема 22. Приложения определенного интеграла к решению вопросов с-х. производства. | 9 | 1 | 8 | |
| Самоподготовка к текущему контролю+зачет | 104 | |||
| Всего за 1семестр | 108 | 2 | 2 | 104 |
| 2-й семестр | ||||
| Раздел 7. Функции нескольких переменных. | 10 | 10 | ||
| Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных. | 5 | 5 | ||
| Тема 24.Условный экстремум функции двух переменных. Тема 25.Производная по направлению. Градиент функции. | 5 | 5 | ||
| Раздел 8. Комплексные числа. | 8 | 8 | ||
| Тема 26. Комплексные числа. Основные действия над комплексными числами. Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера. Тема 28. Разложение многочлена на множители в случае комплексных корней. | 8 | 8 | ||
| Раздел 9. Численные методы. | 30 | 30 | ||
| Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол. | 10 | 10 | ||
| Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона | 10 | 10 | ||
| Тема34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. Тема35. Метод Франка-Вулфа. Метод штрафных функций. Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений | 10 | 10 | ||
| Раздел 10. Дифференциальные уравнения первого порядка. | 26 | 26 | ||
| Тема 37. Дифференциальное уравнение первого порядка с разделяющимися неизвестными. Тема38.Однородные дифференциальные уравнения первого порядка. | 8 | 8 | ||
| Тема 39. Линейное дифференциальное уравнение первого порядка. Метод Бернулли. Тема 40. Линейное дифференциальное уравнение первого порядка. Метод Лагранжа. | 8 | 8 | ||
| Тема 41. Дифференциальные уравнения первого порядка в полных дифференциалах. Тема 42. Дифференциальные уравнения в вопросах с-х. производства. | 10 | 10 | ||
| Раздел 11. Ряды. | 8 | 8 | ||
| Тема 43. Числовые ряды. Основные понятия. Признаки сходимости. Тема 44. Степенные ряды. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд Тейлора (Маклорена) Тема 45. Гармонический анализ. Ряды Фурье. | 8 | 8 | ||
| Раздел12. Теория вероятностей и математическая статистика | 26 | 2 | 2 | 22 |
| Тема 46. Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. | 2 | 2 | ||
| Тема 47. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. | 3 | 1 | 2 | |
| Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа. | 3 | 1 | 2 | |
| Тема49.Случайные величины. Дискретная случайная величина. Законы распределения. Тема50.Числовые характеристики. Неравенство Чебышева. Закон больших чисел. | 2 | 2 | ||
| Тема 51. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Показательное и равномерное распределения. | 2 | 2 | ||
| Тема 52. Основы математической статистики. Выборочный метод Основные выборочные характеристики статистического распределения | 2 | 2 | ||
| Тема 53. Статистические оценки параметров распределения. Точечные и интервальные оценки. | 2 | 2 | ||
| Тема 54.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов | 2 | 2 | ||
| Тема 55. Линейная регрессия со сгруппированными данными в задачах с-х производства Линейная регрессия с несгруппированными данными. | 3 | 1 | 2 | |
| Тема 56.Дисперсионный анализ в анализ в вопросах землеустройства и кадастровых расчетах. Тема 57.Многомерный кластерный анализ. | 5 | 1 | 4 | |
| Самоподготовка к текущему контролю | 95 | 95 | ||
| Подготовка к экзамену | 9 | 9 | ||
| Всего за 2 семестр. | 108 | 2 | 2 | 104 |
| Итого за учебный год | 216 | 4 | 4 | 208 |
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
Математика
| Направление: | 21.03.02 «Землеустройство и кадастры» |
| Профили: | Землеустройство |
| Уровень подготовки | Бакалавриат |
Курс 1
Семестры 1-2
Калуга, 2016
Составители: к. п. н., доцент Жукова И.С « » 2016г.
Программа разработана в соответствии с ФГОС ВО по направлению подготовки 21.03.02 «Землеустройство и кадастры». Рабочая программа дисциплины соответствует учебному плану 2016 г. начала подготовки.
Программа обсуждена на заседании кафедры «Высшей математики и экономической кибернетики»
Зав. кафедрой Мишин П.Н., к.э.н., доцент
протокол № « » 2016г.
Проверено:
Начальник УМЧ _____________________доцент О.А. Окунева
Лист согласования рабочей программы
Декан агрономического факультета
к.биол.н. , доцент Малахова С.Д.
« » 2016г.
Программа принята учебно-методической комиссией по направлению подготовки
21.03.02 “ Землеустройство и кадастры”, протокол № ____
Председатель учебно-методической комиссии по направлению подготовки
Сихарулидзе Т.Д., доцент , к. с-х. н. « » 2016г
Заведующий выпускающей кафедрой Слипец А.А., к.биол.н., доцент
« » 2016г
Оглавление
Аннотация……………………………………………………………………………… 5
1. Требования к уровню освоения дисциплины и ее место в структуре образовательной программы…………………………………………………………… 6
1.1.Требования к уровню освоения дисциплины (планируемые результаты обучения) …………………………………………………………………………………………… 6
1.2. Место дисциплины в структуре образовательной программы…………… …… 6
2. Цели и задачи дисциплины. Требования к результатам освоения дисциплины.6
3. Организационно-методические данные дисциплины (виды учебной работы и их трудоемкость)………………………………………………………………………….. 7
4. Структура и содержание дисциплины…………………………………………………… 8
4.1Структура дисциплины……………………………………………………….……. .8
4.2. Трудоёмкость разделов и тем дисциплины…………………………………… 13
4.3.Содержание разделов дисциплины………………………........................ ...17
4.4. Лабораторные/ практические/ семинарские занятия …………………..…… ....20
4.5. Самостоятельное изучение разделов дисциплины……………………………………… …36
4.5.1. Перечень вопросов для самостоятельного изучения………………………………………36
4.5.2. Курсовые проекты (работы)/ контрольные работы/ расчетно-графические работы/ учебно-исследовательские работы………………………………………………………………………………43
5. Взаимосвязь видов учебных занятий……………………………………………. ..45
6. Учебно-методическое и информационное обеспечение дисциплин 45
6.1. Основная литература …………………………………………………………………………… 45
6.2. Дополнительная литература………………………………………………………………… 45
6.3. Методические указания, рекомендации и другие материалы к занятиям.. ………46
6.4 Интернет-ресурсы……………………………………………………………………….46
7. Критерии оценки знаний, умений, навыков и заявленных компетенций .. 47
8. Материально-техническое обеспечение дисциплины………………………………….52
9. Методические рекомендации преподавателям по организации обучения дисциплины.53
10.Методические рекомендации студентам по самостоятельной работе………………..53
Аннотация
. В рабочей программе отражены темы теоретических основ математики применительно к профессиональной подготовке 21.03.02 “ Землеустройство и кадастры”. Предмет математика служит фундаментальной базой вузовского образования. Он содержит вопросы алгебры, геометрии, математического анализа, теории вероятностей, численных методов. Основы геометрии, алгебры, являющиеся фундаментальными основами картографии и геодезии. В рабочей программе рассматриваются классические способы определения координат точек на основе формул аналитической геометрии и численных методов. Приводятся способы определения площадей земной поверхности на основе основных положений математического анализа.
Студентам предлагается для изучения теория наилучшего приближения функции с помощью многочленов, создателем которой является русский математик П.Л. Чебышев, которая в настоящее время является могучим средством исследования. Все это позволит теорию и методику определения площадей земельных участков, создания топографических карт и кадастровых расчетов к ним поставить на высокую научную основу. Вопросы численных методов, в частности задачи оптимизации, изучающиеся на основе симплекс-метода, метода Жордана-Гаусса, метода Франке-Вулфа и штрафных функций позволят будущему специалисту определять координаты оптимальной точки не только на плоскости, но и в пространстве. Это позволит будущему специалисту разбираться в вопросах применимости математики как к землеустройству и кадастровым расчетам, так и к вопросам управления персоналом, в вопросах экономической эффективности, плановости предприятия, на котором ему придется работать, к возможности применения в работе средств вычислительной техники.
Изучение элементов теории вероятностей и математической статистики, методики расчета погрешности результатов измерений, конкретное построение доверительных интервалов для измеряемой величины, исследование линейной корреляции переменных величин, методов предельного перехода обеспечивает подготовку студентов для исследовательских проектов.
Изучение всех, выше указанных сложных математических приемов не возможно без серьезной математической подготовки. Это налагает большую ответственность на студентов, изучающих этот курс.
Вместе с тем, в процессе учебной деятельности через предмет математика студент совершенствует свое личностное развитие: успехи в учебе способствуют повышению уровня личных притязаний, решение сложных задач способствует умению работать в коллективе, объективно относиться к своим ошибкам. При выборе правильных, рациональных методов, приемов, средств учебной работы со студентом приоритетным направлением является рассмотрение тех компетенций, которые необходимо приобрести студенту в ходе его профессиональной подготовки.
1. Требования к уровню освоения дисциплины и ее место
в структуре образовательной
Программы
1.1. Требования к уровню освоения дисциплины (планируемые результаты обучения)
Реализация в дисциплине «математика» требований ФГОС ВО, ОПОП ВО и Учебного плана по направлению подготовки 21.03.02 “ Землеустройство и кадастры» должна формировать следующие компетенции:
(ОК-7)- способностью к самоорганизации и самообразованию;
(ПК-6) – способностью проведения и анализа результатов исследований и новых разработок.
|
|
Предлагаемый компетентностный подход, рассматривая, возможность формирования у студентов выше указанных компетенции предусматривает, что студент владеет культурой мышления, обладает способностью к восприятию, обобщению и анализу информации, умеет логически верно, аргументировано и ясно формулировать свою мысль.
1.2. Место дисциплины в структуре образовательной программы.
Предшествующими курсами, на которых непосредственно базируется дисциплина «математика» является школьный курс математики.
Дисциплина «матаматика» является основополагающим для изучения следующих дисциплин: экономико-математические методы и моделирование, прикладная геодезия. Особенностью дисциплины является научность, возможность применения математических методов для методики определения площадей земельных участков, создания топографических карт и кадастровых расчетов.
Контроль знаний студентов проводится в форме текущей и промежуточной аттестации. Текущая аттестация студентов – оценка знаний и умений проводится постоянно на практических занятиях при решении студентами задач у доски, с помощью тестовых заданий, контрольных работ, письменного опроса и оценки индивидуальных заданий.
Промежуточная аттестация студента проводится в форме зачета в 1-м семестре и в форме экзамена – во 2-м семестре.
2. Цели и задачи дисциплины. Требования к результатам освоения дисциплины.
Целью дисциплины «математика» является освоение студентами теоретических и практических знаний и приобретение умений и навыков в области математики для дальнейшего применения этих знаний и навыков учебной работы в изучении дисциплин профессиональной направленности.
Внутренние требования: В результате изучения дисциплины «Математика» студент должен:
Знать: - основные понятия и инструменты алгебры и геометрии и методов математического анализа теории вероятностей и математической статистики и численных методов, позволяющих теорию и методику определения площадей земельных участков, создания топографических карт и кадастровых расчетов к ним поставить на высокую научную основу.
Уметь: -систематизировать учебный материал при работе с литературой; уметь своевременно выполнять задания и осуществлять подготовку к письменному опросу и контрольным работам;
- решать типовые математические задачи применительно к вопросам с/.х. производства:
-обрабатывать эмпирические и экспериментальные данные и делать выводы (определять коэффициенты корреляции методом наименьших квадратов и строить математическую модель линейной и нелинейной зависимости);
-использовать методики расчета погрешности результатов измерений, конкретное построение доверительных интервалов для измеряемой величины, исследование линейной корреляции переменных величин, уметь использовать методы предельного перехода;
-определять площади земной поверхности;
-с помощью методов Жордана-Гаусса, метода Франке-Вулфа и штрафных функций определять координаты оптимальной точки не только на плоскости, но и в пространстве.
Владеть: - культурой мышления, обладает способностью к восприятию, обобщению и анализу информации;
- основными приёмами обработки экспериментальных данных
- методами математического анализа; математическими, количественными методами решения типовых профессиональных задач (находить экстремум функции одной и двух переменных, находить и строить асимптоты к графику функции; методом хорд и касательных и другими численными методами)
- методами проверки гипотез, статистическими методами обработки экспериментальных данных.
3. Организационно-методические данные дисциплины (виды учебной работы и их трудоемкость)
Общая трудоёмкость дисциплины составляет 5зач.ед. (189часов), их распределение по видам работ и по семестрам представлено в таблице 1
Таблица 1
| Вид учебной работы | Трудоемкость | |||
| зач. ед. | час. | по семестрам | ||
| №1 | №2 | |||
| Общая трудоемкость дисциплины по учебному плану | 5 | 216 | 108 | 108 |
| Аудиторные занятия | 4 | 144 | 72 | 72 |
| Лекции (Л) | 1 | 36 | 18 | 18 |
| Практические занятия (ПЗ) | 3 | 108 | 54 | 54 |
| Семинары (С) | ||||
| Лабораторные работы (ЛР) | ||||
| Самостоятельная работа (СРС) | 1.25 | 45 | 36 | 9 |
| в том числе: | ||||
| консультации | ||||
| контрольные работы | 0.25 | 9 | 4.5 | 4.5 |
| др. виды | ||||
| Вид контроля: | ||||
| зачет | 0.25 | 9 | + | |
| экзамен | 0,75 | 27 | + | |
| зачет | экзамен | |||
Курс рассчитан на 216 часов, из них – 144аудиторных часа (36 часов лекций , 108 часа практических занятий), 45 часов самостоятельной работы, экзамен-27 часов.
*Применение активных и интерактивных образовательных технологий в учебном процессе приведены в таблице № 2 приложения.
4.Структура и содержание дисциплины.
4.1 Структура дисциплины.
4.1. Структура дисциплины
| Дисциплина «Математика» | |
| Раздел 1 Линейная алгебра | Раздел 7 Функции нескольких переменных - |
| Раздел 2. Векторная алгебра | Раздел 8– Комплексные числа |
| Раздел 3 – Аналитическая геометрия на плоскости и в пространстве | Раздел 9 – Численные методы. |
| Раздел 4– Функции и пределы | Раздел 10 – Дифференциальные уравнения |
| Раздел 5 – Производная и ее применение | Раздел 11 – Ряды |
| Раздел 6 - Неопределенный и определенный интеграл. | Раздел 12 Теория вероятностей и математическая статистика. |
Рисунок 1 – Содержание разделов дисциплины «математика»
Содержание разделов дисциплины
| |||||||||||||||||||||||||
Рисунок 2 – Раздел 1. «Линейная алгебра»
| Раздел 2 – Векторная алгебра | ||||
| Тема 7. Векторы. Линейные операции над ними. Разложение векторов | Тема 8. Операции над векторами. Евкидово пространство. | |||
Рисунок 3 – Раздел 2. «Векторная алгебра»
| Раздел 3 – Аналитическая геометрия на плоскости и в пространстве | |||||||
|
|
| ||||||
| Тема 9. Метод координат на плоскости. Прямая на плоскости | Тема10. Кривые второго порядка | Тема 11.Аналитическая геометрия в пространстве | |||||
Рисунок 4 – Раздел 3. «Аналитическая геометрия на плоскости и в пространстве»
| Раздел 4– Функции и пределы | |||||||
|
|
| ||||||
| Тема 12. Функции и их графики. Последовательности. Предел числовой последовательности . | Тема 13. Предел функции. Непрерывность функции. Асимптоты. | Тема 14.Методы вычисления пределов. | |||||
Рисунок 5 – Раздел 4. «Функции и пределы»
| Раздел 5 – Производная и ее применение | |||||||
|
|
| ||||||
| Тема15. Производная и дифференциал функции. | Тема16.Исследование функций и построение графиков. Выпуклость функции. | Тема17.Применение производной в вопросах с-х. производства. | |||||
Рисунок 6 – Раздел 5. «Производная и ее применение»
| Раздел 6 – Неопределенный и определенный интеграл. | ||||
| Тема 18. Важнейшие свойства и основные методы интегрирования неопределенных интегралов. | Тема 21.Несобственные интегралы. | |||
| Тема 19.Интегрирование рациональных дробей. | Тема22. Приложения определенного интеграла к решению вопросов с-х. производства. | |||
| Тема 20.Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов. | ||||
Рисунок 7 – Раздел 6. «Неопределенный и определенный интеграл»
| Раздел 7– Функции нескольких переменных | |||||||
|
|
| ||||||
| Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных.
| Тема 24.Условный экстремум функции двух переменных. | Тема 25.Производная по направлению. Градиент функции. | |||||
Рисунок 9 – Раздел 8. «Функции нескольких переменных»
| Раздел 8– Комплексные числа | |||||||
|
|
| ||||||
| Тема 26. Комплексные числа. Основные действия над комплексными числами.
| Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера.
| Тема 28. Разложение многочлена на множители в случае комплексных корней.
| |||||
Рисунок 10 – Раздел 9. « Комплексные числа»
| Раздел 9 – Численные методы | ||||
| Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона. | Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона. | |||
| Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева. | Тема 34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод. | |||
| Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы. Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол. | Тема35. Метод Франка-Вулфа. Метод штрафных функций. | |||
| Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения. | Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. | |||
Рисунок 11 – Раздел 10. «Численные методы»
| Раздел 10 – Дифференциальные уравнения | ||||
| Тема 37. Дифференциальные уравнения с разделяющимися неизвестными. | Тема 40. Линейные дифференциальные уравнения первого порядка. Метод Лагранжа. | |||
| Тема 38. Однородные дифференциальные уравнения первого порядка. | Тема 41. Дифференциальные уравнения первого порядка в полных дифференциалах. | |||
| Тема 39. Линейные дифференциальные уравнения первого порядка. Метод Бернулли. | Тема 42. Дифференциальные уравнения в вопросах с-х. производства. | |||
Рисунок 12 – Раздел 11. «Дифференциальные уравнения»
| Раздел 11– Ряды | |||||||
|
|
| ||||||
| Тема 43. Числовые ряды. Основные понятия. Признаки сходимости.
| Тема 44. Степенные ряды. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд Тейлора (Маклорена) | Тема 45. Гармонический анализ. Ряды Фурье. | |||||
Рисунок 12 – Раздел 11. «Ряды»
| Раздел 12 – Теория вероятностей и математическая статистика | ||||
| Тема 46.Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. Теоремы сложения и умножения вероятностей. | Тема 52. Статистические оценки параметров распределения. Точечные и интервальные оценки. | |||
| Тема 47. Формула полной вероятности. Формула Байеса. | Тема 53.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов. | |||
| Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа. | Тема 54. Линейная регрессия со сгруппированными данными в задачах с-х производства. | |||
| Тема 49. Случайные величины. Дискретная случайная величина. Законы распределения. Числовые характеристики. | Тема 55Линейная регрессия с несгруппированными данными. | |||
| Тема 50. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Показательное и равномерное распределения. |
Тема 56. Дисперсионный анализ в задачах инженерии. | |||
| Тема 51.Основы математической статистики. Выборочный метод Основные выборочные характеристики статистического распределения. | Тема 57. Многомерный кластерный анализ. | |||
Рисунок 13 – Раздел 12. «Теория вероятностей и математическая статистика »
4.2. Трудоёмкость разделов и тем дисциплины
Таблица 2 - Трудоемкость разделов и тем дисциплины
Наименование
Разделов и тем дисциплины
Всего часов на раздел/тему
Аудиторная
Работа
Внеаудиторная работа (СРС)
* Применение активных и интерактивных образовательных технологий представлено в ПРИЛОЖЕНИИ 1.
4.3. Содержание разделов дисциплины
1 СЕМЕСТР
Раздел 1.Линейная алгебра
Тема 1. Матрицы. Операции над матрицами. Определители. Вычисление определителей.
Тема 2. Ранг матрицы. Приведение матрицы к ступенчатому виду. Обратная матрица. Матричные уравнения.
Тема 3. Системы линейных уравнений. Метод обратной матрицы.
Тема 4. Метод Крамера.
Тема 5. Метод Гаусса. Метод Жордана-Гаусса.
Тема 6. Понятие разрешенных и свободных переменных системы. Теорема Кронекера-Капелли.
Раздел 2. Векторная алгебра.
Тема 7.Векторы. Линейные операции над ними. Разложение векторов.
Тема 8. Операции над векторами.
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Евклидово пространство.
Раздел 3. Аналитическая геометрия на плоскости и в пространстве.
Тема 9. Метод координат на плоскости. Деление отрезка в данном отношении. Расстояние от точки до прямой. Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой через две точки, каноническое уравнение прямой, уравнение прямой в отрезках на осях. Угол между двумя прямыми.
Тема 10. Кривые второго порядка. Эллипс. Гипербола. Парабола.
Тема 11.Аналитическая геометрия в пространстве.
Раздел 4. Функции и пределы.
Тема 12.Математические модели. Множества. Функции и их графики. Последовательности. Свойства числовых множеств и последовательностей. Предел числовой последовательности.
Тема 13. Предел функции. Непрерывность функции. Свойства непрерывных функций. Асимптоты.
Тема 14.Методы вычисления пределов.
Раздел 5. Производная и ее применение.
Тема 15. Производная и дифференциал функции.
Тема 16.Исследование функций и построение графиков. Выпуклость функции. Точка перегиба функции.
Тема 17. Применение производной в вопросах с-х. производства.
Раздел 6. Неопределенный и определенный интеграл.
Тема 18.Важнейшие свойства и основные методы интегрирования неопределенных интегралов.
Тема19.Интегрирование рациональных дробей.
Тема 20. Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов.
Тема 21. Несобственные интегралы.
Тема 22. Применение интегрального исчисления к вопросам с-х. производства.
2 СЕМЕСТР
Раздел 7. Функции нескольких переменных.
Тема 23. Функции двух переменных. Частные производные функции. Экстремум функции двух переменных.
Тема 24. Условный экстремум функции двух переменных.
Тема 25.Производная по направлению. Градиент функции.
Раздел 8.
Комплексные числа.
Тема 26. Комплексные числа. Сопряженные комплексные числа. Модуль
комплексного числа. Геометрическая интерпретация комплексного числа.
Основные действия над комплексными числами.
Тема 27. Показательная и тригонометрическая формы комплексных чисел. Формула Эйлера.
Тема 28. Разложение многочлена на множители в случае комплексных корней.
Раздел 9. Численные методы.
Тема 29. Интерполирование. Интерполяционный многочлен Лагранжа. Интерполяционная формула Ньютона.
Тема 30.Численное дифференцирование. О наилучшем приближении функций многочленами. Многочлены Чебышева.
Тема 31. Методы минимизации функции одной переменной. Метод деления отрезка пополам. Метод золотого сечения. Симметричные методы .Метод ломаных. Метод покрытий. Метод хорд и касательных. Метод парабол.
Тема 32. Метод поиска глобального минимума. Метод стохастической аппроксимации Примеры наилучшего равномерного приближения.
Тема 33. Численное интегрирование. Метод неопределенных коэффициентов. Квадратурная формула Симпсона.
Тема 34. Градиентный метод. Метод наискорейшего градиентного спуска. Симплексный метод.
Тема 35. Метод Франка-Вулфа. Метод штрафных функций.
Тема 36. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений.
3 СЕМЕСТР
Раздел 10.Дифференциальные уравнения.
Тема 37.Дифференциальные уравнения первого порядка с разделяющимися неизвестными.
Тема 38. Однородные дифференциальные уравнения первого порядка.
Тема 39. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.
Тема 40. Линейные дифференциальные уравнения первого порядка. Метод Лагранжа.
Тема 41. Дифференциальные уравнения первого порядка в полных дифференциалах.
Тема 42. Дифференциальные уравнения в вопросах с-х. производства.
Раздел 11. Ряды.
Тема 43. Числовые ряды. Основные понятия. Признаки сходимости.
Тема 44. Степенные ряды. Ряды Тейлора и Маклорена . Разложение
элементарных функций в ряд Тейлора (Маклорена).
Тема 45. Гармонический анализ. Ряды Фурье.
Раздел 12. Теория вероятностей и математическая статистика.
Тема 46. Классическое и статистическое определение вероятности случайного события. Элементы комбинаторики. Теоремы сложения и умножения вероятностей.
Тема 47. Формула полной вероятности. Формула Байеса.
Тема 48. Повторные испытания. Формула Бернулли. Локальная и интегральная теоремы Лапласа.
Тема49.Случайные величины. Дискретная случайная величина. Законы распределения.
Биномиальное распределение, распределение Пуассона, Лапласа. Понятие наивероятнейшего числа испытаний. Закон больших чисел в формуле Чебышева. Числовые характеристики.
Тема 50. Непрерывная случайная величина. Законы распределения. Числовые характеристики. Нормальное распределение. Правило трёх сигм.
Показательное и равномерное распределения непрерывной случайной величины.
Тема 51. Основы математической статистики. Выборочный метод. Основные выборочные характеристики статистического распределения.
Тема 52. Статистические оценки параметров распределения. Точечные и интервальные оценки.
Тема53.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов.
Тема 54. Линейная регрессия со сгруппированными данными в задачах с-х производства.
Тема 55.Линейная регрессия с несгруппированными данными.
Тема 56.Дисперсионный анализ в вопросах землеустройства и кадастровых расчетах.
Тема 57.Многомерный кластерный анализ.
Лабораторные/ практические/ семинарские занятия
Таблица 3 - Содержание лабораторного практикума/практических занятий/семинарских занятий и контрольных мероприятий
| № п/п | № раздела и темы дисциплины | № и название лабораторных/ практических/ семинарских занятий с указанием контрольных мероприятий | Вид контрольного мероприятия | Кол-во часов |
| 1. | ||||
Раздел 1. Линейная алгебра.
2.
Раздел 2. Векторная алгебра.
3.
Раздел 3. Аналитическая геометрия на плоскости и в пространстве.
4.
Раздел 4. Функции и пределы
5.
Дата: 2019-02-19, просмотров: 310.

 Укажите график периодической функции.
Укажите график периодической функции.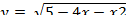 + lg (x+3)
+ lg (x+3)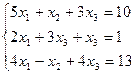
 а) (1;-1;2) б)(3:-3:5) в)(-1;2;4)
а) (1;-1;2) б)(3:-3:5) в)(-1;2;4)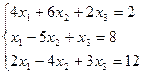
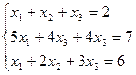

 , то
, то 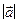 =…
=… ; 2)7; 3) –1; 4)
; 2)7; 3) –1; 4) 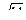 .
.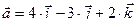 , то
, то 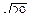 ; 2)3; 3) –4; 4)
; 2)3; 3) –4; 4) 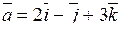
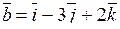 ,
,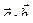 равно: 1)
равно: 1) 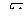 .
.
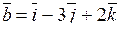
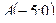 ,
, 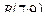 ,
, 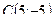
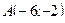 ,
, 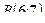 ,
, 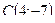

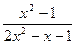 б) 1.
б) 1. 
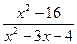
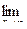
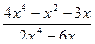 2.
2. 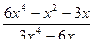
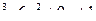 являются: а) -1; 2 б) 3; 1 в) -3; 2
являются: а) -1; 2 б) 3; 1 в) -3; 2  являются: а) 4; 2 б) 3: -3 в) 1; 2
являются: а) 4; 2 б) 3: -3 в) 1; 2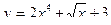 имеет вид …
имеет вид …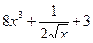 ; 2)
; 2) 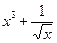 ; 3)
; 3) 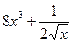 ; 4)
; 4) 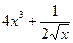 .
.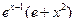 ; 2)
; 2) 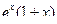 ; 3)
; 3) 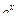 ; 4)
; 4) 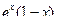 .
.