2. Введение естественных базисных переменных. Построение симплексной таблицы. Определение нулевого плана.
Симплекс-метод. Алгоритм симплекс-метода.
Симплекс-метод - алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком Джорджем Данцигом в 1947 году.
Идея симплексного метода состоит в том, что поставленная описательная задача переводится в математическую форму. Математическая формулировка задачи содержит уравнение целевой функции с указанием желаемого результата - определение минимума или максимума целевой функции; системы линейных ограничений, заданных равенствами или неравенствами. Полученное математическое описание приводят к матричному виду. Затем матричное описание задачи приводят к канонической форме. После того как система линейных уравнений приведена к канонической форме, приступают к решению задачи линейного программирования. Алгоритм решения этой задачи состоит из последовательности построения матриц. Каждый шаг решения приближает к получению желаемого результата.
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Алгоритм симплекс-метода
1. Приводим систему ограничений к каноническому виду (когда система ограничена). Причём в системе можно выделить единичный базис.
2. Находим первоначальный опорный план (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А1, А2,…, Аn. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний Сnm);
3. Строим симплексную таблицу (симплекс-таблица матрица, служащая средством перебора допустимых базисных решений (невырожденной) задачилинейного программирования при ее решении симплексным методом. Образуется из матрицы коэффициентов системы уравнений линейного программирования, приведенной к канонической форме, последовательное ее преобразование по так называемому симплексному алгоритму позволяет заограниченное количество шагов (итераций) получать искомый результат - план, обеспечивающий экстремальное значение целевой функции).
4. В симплексной таблице проверяем вектора на отрицательность, т.е. оценки Zj – С j записанные в 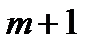 строке должны быть ≤ 0 (на минимум), Zj – С j ≥ 0 (на максимум). Если оценки удовлетворяют условиям оптимальности то задача решена.
строке должны быть ≤ 0 (на минимум), Zj – С j ≥ 0 (на максимум). Если оценки удовлетворяют условиям оптимальности то задача решена.
5. Если для некоторых векторов нарушаются условия оптимальности, то необходимо ввести в базис вектор, которому соответствует:
max [θ0 j ( Zj – С j )] ; min [θ0 j ( Zj – С j )] ; θ0 j = min 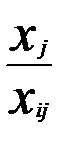 , где х i > 0
, где х i > 0
Элемент вектора θ j который соответствует θ0 j называется разрешающим; строка и столбец в которых он находится, называется направляющим, из базиса уходит вектор, стоящий в направляющей строке.
6. Найдём коэффициент разложения для всех векторов в новом базисе. Применим метод Джордано Гаусса
Проверим на оптимальный опорный план. Если оценка удовлетворяет условиям оптимальности, то задача решена, если нет, то выполняются пункты 5-7.
2. Введение естественных базисных переменных. Построение симплексной таблицы. Определение нулевого плана.
Симплекс-метод наиболее эффективен при решении сложных задач и представляет итерационный (шаговый) процесс, начинающийся с нулевого (опорного) решения (вершины n-мерного многогранника). Далее в поисках оптимального варианта плана предполагается движение по угловым точкам (вершинам многогранника) до тех пор, пока значения целевой функции не достигнет максимальной (минимальной) величины. Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота при ограниченных ресурсах сырья.
Предприятие реализует n товарных групп, располагая m ограниченными материально-денежными ресурсами bi ≥0 (1 ≤ i ≤ m) . Известны расходы ресурсов каждого i- вида на производство и реализацию единицы товара каждой группы, представленные в виде матрицы (aij) и прибыль, получаемая предприятием от реализации единицы товара j-группы, входящая в целевую функцию Z(X). Метод линейного программирования не отличается от системы (1) - (2):
Z(X) = с1 Х1 + с2 Х2 + с3 Х3 + … +сn Хn →max(min) (1)
a11 X1 + a12 X2 +…a1n X n ≤ b1,
а21 X1 + a22 X2 +…a2n X n ≤ b2 (2)
am1 X1 + am2 X2 +…a mn X n ≤ b m,
X1≥0 X2≥0 X3≥0 …X n ≥0
Этапы решения поставленной задачи симплексным методом включают:
1) Составление нулевого опорного плана. Вводим новые неотрицательные (базисные) переменные, благодаря которым система неравенств (2) становится системой уравнений:
a11 X1 + a12 X2 +…a1n X n + Xn+1 = b1
a21 X1 + a22 X2 +…a2n X n + Xn+2 = b2 (3)
……………………………………..
am1 X1 + am2 X2 +…a mn X n + Xn+m = b m,
Если принимать вводимые переменные за векторы-столбцы, то они представляют собой единичные (базисные) векторы. Отметим, что базисные переменные имеют простой физический смысл – это остаток конкретного ресурса на складе при заданном плане выпуска продукции, поэтому данный базис называют естественным. Решаем систему (3) относительно базисных переменных:
Xn+1 = b1, -a11 X1 - a12 X2 -…a1n X n
Xn+2 = b2 - a21 X1 - a22 X2 -…a2n X n (4)
………………………………………..
Xn+m = b m, - am1 X1 + am2 X2 +…a mn X n
Целевую функцию перепишем в виде
Z(X) = 0-(-с1Х1-с2Х2-с3Х3-…-сnХn) (5)
Полагая, что искомые основные переменные Х1 = X2 = X3 = … = Xn = 0, получаем нулевой опорный план Х = (0, 0, …0, b1, b2, b3 … bm ), при котором Z(X) = 0 (все ресурсы на складе, ничего не производится). Заносим план в симплексную таблицу.
| План | Базис | Ci/Cj | Знач. Xi | X1 | X2 | Xn | Xn+1 | Xn+2 | Xn+3 | Qmin |
| 0 | Xn+1 | 0 | b1 | a11 | a12 | a13 | 1 | 0 | 0 | b1/ a12 |
| Xn+2 | 0 | b2 | a21 | a22 | a23 | 0 | 1 | 0 | b2/ a22 | |
| Xn+3 | 0 | b3 | a31 | a32 | a33 | 0 | 0 | 1 | b3/ a32 | |
| Z(X) = 0 | -C1 | - C2 | - C3 | 0 | 0 | 0 | Индекс. строка | |||
2) Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что определяет ведущий столбец и показывает – какая переменная на следующей итерации (шаге) перейдет из основных (свободных) в базисные (фактически выбирается товарная группа, чья реализация приносит максимальный доход). Затем запасы сырья bi делим на соответствующие коэффициенты затрат, результаты заносим в таблицу и определяем минимальное значение Qmin (выбирается ресурс, чей запас наиболее сильно ограничивает выпуск выбранной товарной группы). Это значение выделяет ведущую строку и переменную Хi , которая при следующем шаге (итерации) выйдет из базиса и станет свободной.
3) Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала заменим в базисе Хj на Хi ведущего столбца. Разделим все элементы ведущей строки на разрешающий элемент (РЭ), в результате чего на месте РЭ в ведущей строке будет 1. Так как Хi стал базисным, то остальные его коэффициенты должны быть равны 0. Новые элементы этого плана находятся по правилу прямоугольника
НЭ=СЭ – (А*В)/РЭ (6)
Оценка полученного плана производится по коэффициентам индексной строки: если они все положительны, то план оптимален, если нет, то план можно улучшить, производя следующую итерацию (шаг).
Пример. На приобретение оборудования для производственного участка выделено 20 тыс.руб. Оборудование может быть размещено на площади, не превышающей 72 кв.м. Можно заказать оборудование двух типов: типа А, требующие производственную площадь 6кв.м и дающие 6 тыс.ед. продукции в смену ( цена 5000 руб.) и типа В, требующие площадь 12 кв.м и дающие 3тыс.ед., (цена 2000 руб.). Каков оптимальный план приобретения оборудования, обеспечивающий максимальную производительность участка?
Обозначим количество приобретаемого оборудования типа А и В через Х1 и Х2 соответственно.
Производительность участка (целевая функция) : Z(X) =6Х1+3Х2.
Основные ограничения связаны
с денежными средствами : 5Х1+2Х2 ≤ 20,
с площадью производственного участка : 6Х1+12Х2 ≤ 72.
Вводим новые базисные переменные Х3 (остаток денежных средств после закупки оборудования) и Х4 (остаток площадей после размещения оборудования) и перепишем ограничения в виде системы уравнений:
5X1+2Х2+X3=20 (X3=20 – 5X1 - 2X2)
6Х1+12Х2+X4 = 72 (X4=72 – 6X1 – 12X2)
При этом функция цели: Z(X) =6Х1+3Х2+0Х3+0Х4.
Составляем опорный (0-ой) план: Х= (0, 0, 20, 72), т.е. пока ничего не приобретено (деньги не потрачены, площади пустуют). Составляем симплексную таблицу
| План | Базис | Ci/Cj | Знач. Xi | X1 | X2 | X3 | X4 | Qmin | |||
| 0 | X3 | 0 | 20 | 5 | 2 | 1 | 0 | 20/5=4 | |||
| X4 | 0 | 72 | 6 | 12 | 0 | 1 | 72/6=12 | ||||
| Z(X) = 0 | - 6 | - 3 | 0 | 0 | Индексная строка | ||||||
| 1 | →X1 | 6 | 4 | 1 | 0,4 | 0,2 | 0 | 4/0,4=10 | |||
| X4 | 0 | 48 | 0 | 9,6 | -1,2 | 1 | 48/9,6=5 | ||||
| Z(X) = 6*4=24 | 0 | -0,6 | 1,2 | 0 | Индексная строка | ||||||
| 2 | X1 | 6 | 2 | 1 | 0 | 0,25 | -1/24 | - | |||
| →X2 | 3 | 5 | 0 | 1 | -1/8 | 5/48 | - | ||||
| Z(X) =6*2+3*5=27 | 0 | 0 | 9/8 | 1/16 | Индексная строка | ||||||
Очевидно, что ведущий столбец соответствует Х1, так как имеет самый большой индекс 6. Находим минимальное значение Qmin = 4 ( самое жесткое ограничение ресурса), определяя ведущую строку, показывающую, что из базисных переменных выводится Х3, а вместо нее вводится Х1. Пересчитываем элементы ведущей строки, разделив их на 5, а по формуле (6) определяем элементы второй и индексной строк. Целевая функция для 1-ого плана равна Z(X) = 6*4+3*0 = 24.
Однако, один из коэффициентов индексной строки для столбца Х2 остается отрицательным -0,6, следовательно данный план не оптимален, и требуется еще одна итерация (шаг) для его улучшения. Выбираем ведущим 2-ой столбец и по минимальному значению Qmin = 5 определяем ведущую строку с базисной переменной Х4. Выполнив те же преобразования, получаем 2-ой план, который будет оптимальным, так как все индексные коэффициенты положительны.
Проанализируем полученные результаты. При оптимальном решении целевая функция имеет максимальное значение 27тыс.руб., при этом оба ресурса выведены из базиса, следовательно израсходованы полностью.
Убедимся в этом: 5*2+2*5 = 20 тыс.руб., 6*2+12*5=72 кв.м. Искомое решение Х= (2; 5;0;0).Так бывает далеко не всегда.
Лекция № 10
Тема: Закрытая транспортная задача
План:
1. Математическая формулировка закрытой транспортной задачи. Определение необходимого количества неизвестных.
2. Этапы определения плана решения транспортной задачи.
Дата: 2019-02-19, просмотров: 694.