Математическая статистика – наука о способах получения выводов из данных опыта, полностью опирается на методы теории вероятностей, в этом смысле теория вероятностей является частью математической статистики.
Основные разделы математической статистики.
1. Теория оценок. Эта теория дает подходы к приближенному вычислению параметров случайных величин (матема-тического ожидания, дисперсии, ковариации и т.д.) по данным опыта.
2. Статистическая проверка гипотез. Эта теория дает подходы к проверке справедливости интересующих нас гипотез по данным опыта.
3. Дисперсионный анализ. Эта теория дает подходы к изучению слабых (статистических) зависимостей между величинами.
Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
В математической статистике применяются следующие термины. Множество всех возможных значений случайной величины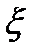 
называется генеральной совокупностью.
Пусть с испытанием связана случайная величина 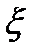и пусть в результате серии n независимых испытаний получен набор значений :
.
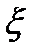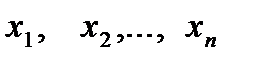Данный набор чисел называется выборкой из генеральной совокупности, число n называется объемом выборки, числа называются элементами выборки. Элементы выборки, расположенные в порядке возрастания называются вариационным рядом:
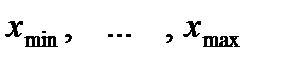- вариационный ряд.
Число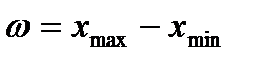 
называется размахом выборки.
Выполним следующие построения:
. . . 
. . . 
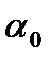
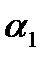
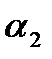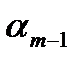
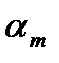
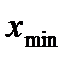
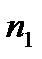
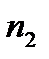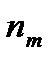
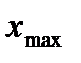
рис. 1
1) разделим отрезок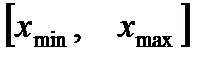 
на некоторое число m интервалов одинаковой длины 
.
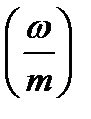2) подсчитаем число элементов выборки, попадающих в каждый интервал:
- частоты попадания в интервал.
Очевидно,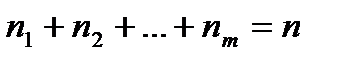 
.
3) составим таблицу
Таблица 1.
.
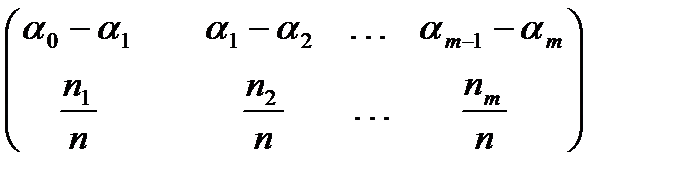Элементы второй строки называются относительными частотами попадания в интервал. Эта таблица называется выборочным распределением случайной величины .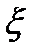
Очевидно,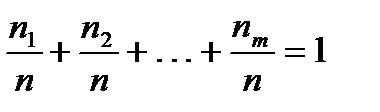 
.
4) изобразим выборочное распределение на графике
f * ( x )
|
|
|
. . .
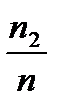
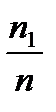
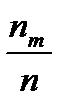
| 0 |
х
. . . 
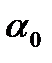
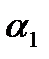
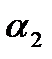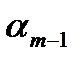
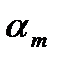
рис. 2
За единицу масштаба на оси абсцисс примем длину интервала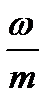 
. Очевидно, площадь построенной ступенчатой фигуры равна единице.
Построенный график называется гистограммой относительных частот и представляет собой выборочный аналог плотности вероятности случайной величины.
Выборочная функция распределения
Построим выборочный аналог функции распределения F (x).
Для этого вначале на каждом интервале (рис. 1) выберем середину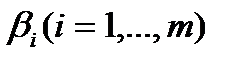 
и составим таблицу.
Таблица 2.
.
|
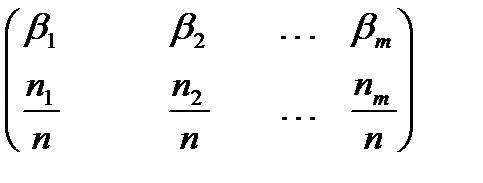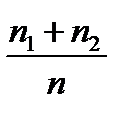
| F*(x) |
| 0 |
| b1 b2 b3 × × × bm-1 bm |
| × × × |
| x |
| 1 |
|
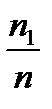
рис. 3
На оси ординат откладываем накопленные относительные частоты. Кружочки на графике означают, что соответствующие точки выброшены.
Можно доказать, что при достаточно большом объеме выборки и при достаточно мелком делении интервалов с практической достоверностью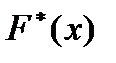 
близка к истинной функции распределения F (x).
Лекция № 5
Тема: Оценка параметров распределения.
План:
1. Выборочные оценки параметров случайной величины. Основные требования к оценкам.
2. Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации.
1. Выборочные оценки параметров случайной величины. Основные требования к оценкам
На практике эти параметры находятся приближенно по данным опыта.
Пусть с испытанием связана случайная величина 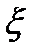с неизвестным параметром 
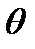, и пусть в результате серии независимых испытаний получена выборка 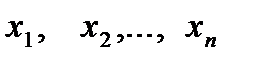. В качестве приближенного значения параметра 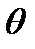принимают надлежащим образом выбранную комбинацию элементов выборки .
.
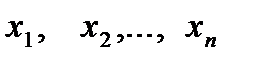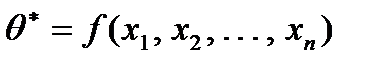Величина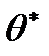 
называется выборочной оценкой параметра .
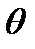К выборочным оценкам предъявляются следующие три основных требования: состоятельность, несмещенность, эффективность.
Чтобы были понятны даваемые далее определения этих понятий, обратим внимание на следующее: до выполнения испытаний числа 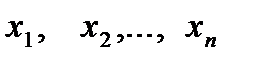представляют собой независимые случайные величины, подчиненные одному и тому же закону распределения, совпадающему с законом распределения случайной величины 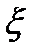, поэтому 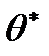также является случайной величиной, и имеет смысл говорить о математическом ожидании, дисперсии, СКО и т.д. случайной величины .
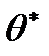Дата: 2019-02-19, просмотров: 526.
